中国邮递员问题的深入剖析与算法实现(附例题及MATLAB、LINGO代码)
中国邮递员问题的深入剖析与算法实现
- 一、研究背景
- 1.1 哥尼斯堡七桥问题
- 1.2 欧拉图
- 1.3 中国邮递员问题
- 二、中国邮递员问题深入解读
- 2.1 问题重述
- 2.2 奇偶点图上作业法[^1]
- 2.3 最小二分匹配法
- 1) 针对无向图
- 2) 针对有向图
- 2.4 $fleury$算法
- 三、经典中国邮递员问题的具体实现
- 3.1 最小权匹配的实现
- 1)$floyd$算法
- 2)最小权匹配算法
- 3.2 $fleury$算法的实现
- 1) $fleury$算法
- 2)桥的判断
- 3)连通图判断
- 四、广义中国邮递员问题
- 4.1 广义中国邮递员问题的介绍
- 4.2 图的划分策略
- 4.3 模型可解化
- 1)针对无向图
- 2) 针对有向图
- 4.4 公平性拓展
- 五、广义中国邮递员问题的实践
- 5.1 图的划分算法
- 5.2 题目实例
一、研究背景
1.1 哥尼斯堡七桥问题
哥尼斯堡七桥问题是18世纪著名古典数学问题之一。其描述为:
在哥尼斯堡的一个公园里,有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。问是否可能从这四块陆地中任一块出发,恰好通过每座桥一次,再回到起点?
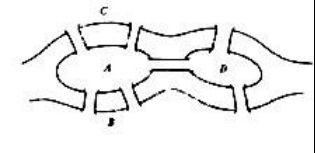
欧拉于1736年研究并解决了此问题,他把问题归结为“一笔画”问题,并证明上述走法是不可能的。
欧拉的论点是:除了起点以外,每一次当一个人由一座桥进入一块陆地(或点)时,他(或她)同时也由另一座桥离开此点。所以每行经一点时,计算两座桥(或线),从起点离开的线与最后回到始点的线亦计算两座桥,因此每一个陆地与其他陆地连接的桥数必为偶数。
而若将哥尼斯堡七桥问题中的每一块地看作一个点,而每一座桥看作一条线,则可得到下图。
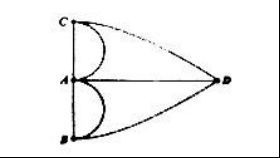
不难看出,上图中的每一点所连接的线数目皆为奇数,故所述任务无法完成。
1.2 欧拉图
1736年29岁的欧拉向圣彼得堡科学院递交了《哥尼斯堡的七座桥》的论文,在解答问题的同时,开创了数学的一个新的分支——图论与几何拓扑,也由此展开了数学史上的新历程。
由于欧拉对于哥尼斯堡的七桥问题的解决,图论中把可完成“一笔画”的图称作欧拉图(Euler Graph),由此又有了欧拉回路(Euler Circuit)与欧拉路径(Euler Path)的概念。
欧拉路径是指通过图中所有边的简单路,而欧拉回路指闭合的欧拉路径。拥有欧拉回路的图即可称为欧拉图。
1.3 中国邮递员问题
一个邮递员从邮局出发,要走完他所管辖范围内的每一条街道至少一次再返回邮局,如何选择一条尽可能短的路线?
这就是中国邮递员问题(Chinese Postman Problem),简称CPP问题,其命名是因为中国数学家管梅谷在1962年首先提出了这个问题。
二、中国邮递员问题深入解读
2.1 问题重述
中国邮递员问题可用图论语言叙述为:在一个具有非负权的带权连通图 G G G中,找出一条总权重最小的环游,这种环游称为最优环游。
① G G G是欧拉图,则 G G G的任意欧拉回路都是最优环游。
② G G G不是欧拉图,则 G G G的任意一个环游必定通过某些边不止一次。将边 e e e的两个端点再用一条权为 w ( e ) w(e) w(e)的新边连接时,称边 e e e为重复的。此时CPP问题与下述问题等价:
若 G G G是给定的有非赋权的赋权连通图,
⑴用添加重复边的方法求 G G G的一个欧拉赋权母图 G ∗ G^* G∗,满足
m i n ∑ e ∈ E ( G ∗ ) − E ( G ) w ( e ) min\sum_{e\in E(G^*)-E(G)} w(e) mine∈E(G∗)−E(G)∑w(e)
⑵求 G ∗ G^* G∗的欧拉回路。
2.2 奇偶点图上作业法1
1960年我国管梅谷发表于数学学报上的论文“奇偶点图上作业法”,是针对于中国邮递员问题的最早论文,将关于“一笔画”问题的一些已知结果与物资调拨中的图上作业法的基本思想相结合,得到了CPP问题中添边策略的一种方法。
定义 1 奇偶点图上作业法
①生成初始可行方案:
若图中有奇点,则把它配成对,每一对奇点之间必有一条链,把这条链的所有边作为重复边加到图中去,新图中必无奇点。便给出了第一个可行方案。
②调整可行方案:
使重复边总长度下降.当边 ( w , v ) (w,v) (w,v)上有两条或两条以上的重复边时,从中去掉偶数条,得到一个总长度较小的方案。于是,有:
1)在最优方案中,图的每条边上最多有一条重复边。
2)在最优方案中,图中每个圈上的重复边的总权不大于该圈总权的一半。
③判断最优方案的标准:
一个最优方案一定是满足上述1)和2)的可行方案。反之,一个可行方案若满足上述1)和2),则这个可行方案一定是最优方案。
根据判断标准,对给定的可行方案,检查它是否满足上述条件1)和2)。若满足,所得方案即为最优方案;若不满足,则对方案进行调整,直至上述条件1)和2)均得到满足时为止。
2.3 最小二分匹配法
奇偶点图上作业法是全球范围内研究CPP问题的先驱,他提出了一种添边策略,其中最关键的是指出了一非欧拉图向欧拉图转化的实质是奇点之间的两两匹配,联想到图论二分匹配2中的最大权匹配,本文提出最小权匹配法来完成非欧拉图向欧拉图的转换。
1) 针对无向图
设 G = ( V , E ) G=(V,E) G=(V,E)为一简单无向联通图, D D D为使用 f l o y d floyd floyd算法求得的图的最短路程矩阵, P P P为对应的路径矩阵。
设 V 1 V_1 V1为图 G G G的奇点集,由图论基础知识可证明一简单图的奇点个数为偶数,记其为 n n n。构建二分图 B = ( S , T , E ′ ) B=(S,T,E^{'}) B=(S,T,E′),其中 S = T = V 1 S=T=V_1 S=T=V1, E ′ E^{'} E′的构建如下:
w ( e i j ′ ) = { D S i T j ′ , if S i ≠ T j ∞ , if S i = T j w(e_{ij}^{'}) = \begin{cases} D_{S_iT_j}^{'}, & \text{if $S_i \ne T_j$} \\ \infty, & \text{if $S_i = T_j$} \end{cases} w(eij′)={DSiTj′,∞,if Si̸=Tjif Si=Tj
求该二分图的最小权匹配,引入决策变量 x i j = 0 , 1 x_{ij} =0,1 xij=0,1来表示 S i S_i Si与 T j T_j Tj的匹配关系,若 x i j = 1 x_{ij} =1 xij=1则表示与匹配,反之则不匹配,可建立数学规划模型如下:
m i n w ( e i j ′ ) x i j min \ \ w(e_{ij}^{'})x_{ij} min w(eij′)xij s . t . { ∑ i = 1 n x i j = 1 , j = 1 , 2 , . . . , n ∑ j = 1 n x i j = 1 , i = 1 , 2 , . . . , n x i j = x j i , i = 1 , 2 , . . . , n ; j = 1 , 2 , . . . , n x i j ∈ { 0 , 1 } , i = 1 , 2 , . . . , n ; j = 1 , 2 , . . . , n s.t. \begin{cases} \sum_{i=1}^n x_{ij}=1, &j=1,2,...,n\\ \sum_{j=1}^n x_{ij}=1, &i=1,2,...,n\\ \ x_{ij}=x_{ji},&i=1,2,...,n;j=1,2,...,n\\ \ x_{ij}\in \{0,1\},&i=1,2,...,n;j=1,2,...,n \end{cases} s.t.⎩⎪⎪⎪⎨⎪⎪⎪⎧∑i=1nxij=1,∑j=1nxij=1, xij=xji, xij∈{0,1},j=1,2,...,ni=1,2,...,ni=1,2,...,n;j=1,2,...,ni=1,2,...,n;j=1,2,...,n
由该模型求出奇点集的两两匹配,再结合 f l o y d floyd floyd算法得到的最短路程矩阵对应的路径矩阵,可得到 G G G由生成的最小权欧拉图 G ∗ = ( V , E ∗ ) G^*=(V,E^*) G∗=(V,E∗)。则此时CPP问题的最优目标值已可求出,即是将的边集中的每一条边都走一遍,其值为 L = ∑ i ∈ E ∗ w ( e i ) L=\sum_{i \in E^*}w(e_i) L=i∈E∗∑w(ei)
2) 针对有向图
一个无向图是欧拉图的充要条件是,所有顶点的度数都是偶数,即所有点都是偶点。而有向图是欧拉图的充要条件也是所有顶点都是偶点,但有向图中偶点的定义为出度=入度,则奇点的定义便理应为出度≠入度,下给出求简单有向联通图的转化为欧拉图的最小权匹配模型。
设 G = ( V , E ) G=(V,E) G=(V,E)为一简单有向联通图,记 R i = d i + − d i − R_i=di^+-d_i^- Ri=di+−di−,其中 d i + di^+ di+为顶点 v i v_i vi的出度, d i − di^- di−为顶点 v i v_i vi的入度。
建立顶点集 V + = { v i ∣ v i ∈ V , R i > 0 } V^+=\{v_i|v_i\in V,R_i>0\} V+={vi∣vi∈V,Ri>0}以及 V − = { v i ∣ v i ∈ V , R i < 0 } V^-=\{v_i|v_i\in V,R_i<0\} V−={vi∣vi∈V,Ri<0},设其长度分别为 n + n^+ n+与 n + n^+ n+。构建二分图 B = ( V + , V − , E ′ ) B=(V^+,V^-,E^{'}) B=(V+,V−,E′),其中 S = T = V 1 S=T=V_1 S=T=V1, E ′ E^{'} E′的构建参照无向图,亦由 f l o y d floyd floyd算法得到最短距离矩阵决定。
引入变量 x i j x_{ij} xij,表示从顶点 v j v_j vj到 v i v_i vi新增的链数,建立数学规划模型如下:
m i n w ( e i j ′ ) x i j min \ \ w(e_{ij}^{'})x_{ij} min w(eij′)xij s . t . { ∑ i = 1 n x i j = − R j , j = 1 , 2 , . . . , n − ∑ j = 1 n x i j = R i , i = 1 , 2 , . . . , n + x i j ∈ N , i = 1 , 2 , . . . , n + ; j = 1 , 2 , . . . , n − s.t. \begin{cases} \sum_{i=1}^n x_{ij}=-R_j, &j=1,2,...,n^-\\ \sum_{j=1}^n x_{ij}=R_i, &i=1,2,...,n^+\\ \ x_{ij}\in \ N,&i=1,2,...,n^+;j=1,2,...,n^- \end{cases} s.t.⎩⎪⎨⎪⎧∑i=1nxij=−Rj,∑j=1nxij=Ri, xij∈ N,j=1,2,...,n−i=1,2,...,n+i=1,2,...,n+;j=1,2,...,n−
求出奇点的匹配后,同样可利用1)中同样方法结合 f l o y d floyd floyd算法得到的最短路程矩阵对应的路径矩阵求出由 G G G生成的最小权欧拉图 G ∗ G^* G∗。
2.4 f l e u r y fleury fleury算法
无论是无向图还是有向图,皆通过上述模型求解奇点的最小权匹配并由此构造出对应于原图的最小权欧拉图,由中国邮递员问题中的图论语言描述中推导出的等价问题可知,原问题已转化为求欧拉图的一条欧拉回路。
故本段对如何求欧拉图中的欧拉回路进行研究, f l e u r y fleury fleury算法是一种常用的求欧拉图中一条欧拉回路的算法。
定义 2 f l e u r y fleury fleury 算法
设 G = ( V , E ) G = (V, E) G=(V,E)为一欧拉图,下为 f l e u r y fleury fleury 算法的算法流程:
STEP1 任取 v 0 ∈ V v_0\in V v0∈V ,令 C 0 = v 0 C_0 =v_0 C0=v0 ;
STEP2 假设当前已沿迹 C i = v 0 e 1 v 1 e 2 v 2 ⋯ e i v i C_i =v_0e_1v_1e_2v_2\cdots e_iv_i Ci=v0e1v1e2v2⋯eivi 来到顶点 v i v_i vi ,按照如下规则从边集 E − { e 1 , e 2 , ⋯ , e i } E-\{e_1,e_2,\cdots ,e_i\} E−{e1,e2,⋯,ei}中选取 e i + 1 e_{i+1} ei+1 :
⑴ e i + 1 e_{i+1} ei+1与 v i v_i vi 关联;
⑵ 除非无其他可选边,否则 e i + 1 e_{i+1} ei+1不为图 G i = G − { e 1 , e 2 , ⋯ , e i } G_i=G-\{e_1,e_2,\cdots ,e_i\} Gi=G−{e1,e2,⋯,ei}的割边。
STEP3 当 STEP2 无法继续进行时停止算法。
当算法停止时,得到的迹 C m = v 0 e 1 v 1 e 2 v 2 ⋯ e m v m C_m =v_0e_1v_1e_2v_2\cdots e_mv_m Cm=v0e1v1e2v2⋯emvm为图 G G G的一条欧拉回路,下证明该结论。
定理 1 由 f l e u r y fleury fleury 算法求得的迹必为欧拉回路。
证明
设 C m = v 0 e 1 v 1 e 2 v 2 ⋯ e m v m C_m =v_0e_1v_1e_2v_2\cdots e_mv_m Cm=v0e1v1e2v2⋯emvm为对无向欧拉图 G G G作 f l e u r y fleury fleury 算法求得的一条迹。
先证 C m C_m Cm是回路,显然地,在 f l e u r y fleury fleury 算法中所生成的过程子图 G m G_m Gm中终点 v m v_m vm 的度数为 0,由此可推得 v m = v 0 v_m=v_0 vm=v0,即 C m C_m Cm是一条闭迹,即一条回路。
现假设 C m C_m Cm不是图 G G G 的欧拉回路,并设 S S S是图 G m G_m Gm中度数为正的顶点集合,则 S S S非空,且有 v m ∈ S − v_m\in S^- vm∈S−,此处 S − = V − S S^-=V-S S−=V−S。
设 n n n是满足 v n ∈ S v_n\in S vn∈S, v n + 1 ∈ S − v_{n+1}\in S^- vn+1∈S− 的最大整数。由于 C m C_m Cm 终止于 S − S^- S− ,故 e n + 1 e_{n+1} en+1必定是图 G n G_n Gn中连接 S S S与 S − S^- S−的唯一边,即 e n + 1 e_{n+1} en+1是 G n Gn Gn的一条割边。设 e e e是 G n G_n Gn中与 v n v_n vn相关的另外任意一条边,可知 e e e也是 G n G_n Gn的一条割边,因此也就是 G n ( S ) G _n(S) Gn(S) 的一条割边。
但由于 G n ( S ) = G m ( S ) G_n(S)=G_m(S) Gn(S)=Gm(S),所以 G n ( S ) G_n(S) Gn(S)中所有顶点都为偶点,故 G n ( S ) G_n(S) Gn(S)无割边,这与 C m C_m Cm不是图 G G G 的欧拉回路的假设矛盾。故 C m C_m Cm是图 G G G的一条欧拉回路。
对于有向图的证明方法类似,本文不赘述。
三、经典中国邮递员问题的具体实现
本文所提供的程序代码皆在以下环境运行:
Intel Core i7-4720HQ CPU @2.60GHz
12.0GB RAM
Windows 10 专业版
MATLAB R2014a
3.1 最小权匹配的实现
1) f l o y d floyd floyd算法
function [D,path,min1,path1]=floydf(a,start,terminal)
% --------------------
% a 表示权值矩阵 start 起点 terminal 终点
% ---------------------
% D 表示任意两点间最小路径权值 path 表示路径矩阵
% min1 表示 start 到 terminal 的最小路径权值
% path1 表示 start 到 terminal 的最小路径
% ---------------------
D=a; %赋初值,最小路径权值矩阵开始等于初始的权值矩阵
n=size(D,1);% 顶点数目
path=zeros(n,n); %初始的路径矩阵,全部置为 0
%修改路径矩阵,若两点 ij 之间有边,路径矩阵相应位置置为 j
for i=1:n
for j=1:n
if D(i,j)~=inf
path(i,j)=j;
end
end
end
%插入顶点计算最小路径
for k=1:n % 最多插入 n 个顶点
for i=1:n
for j=1:n
if D(i,k)+D(k,j)<D(i,j) %插入 k 后,得到的两个路径之和比原来的路径权值
小
D(i,j)=D(i,k)+D(k,j); %修改 ij 的路径权值
path(i,j)=path(i,k); %在 ij 路径矩阵中插入 k
end
end
end
end
if nargin==3 %如果输入参数是 3 个
min1=D(start,terminal);%直接从最小路径权值矩阵中读出 start 到 terminal 的最
小路径权值
%下面是构造从 start 到 terminal 的最小路径
m(1)=start;%起点
i=1;%最小路径中顶点序号
path1=[ ]; %开始路径为空
while path(m(i),terminal)~=terminal %表示如果 m(i)和 terminal 之间还有
插入点
k=i+1; %最小路径顶点序号更新(加一个)
m(k)=path(m(i),terminal); %m(i)和 terminal 之间的插入点是 start 到
terminal 最小路径的第 k 个顶点
i=i+1; %序号更新
end
m(i+1)=terminal;%start 到 terminal 最小路径的最后一个顶点是 terminal
path1=m;%生成的最小路径 m 复制给路径 path1
end
2)最小权匹配算法
function [linked,F,PA]=minweightmatch(E)
%--------------------------
% E 为图的邻接矩阵
%--------------------------
% linked 为相互配对的奇点
% F 为新增的路径权值
% PA 为配对奇点之间的最短路径
%--------------------------
% 找出所有奇点
L=length(E);
JD=mod(sum(E>0 & E<inf),2);
p=find(JD==1);
% 弗洛伊德算法求奇点间最短路
[D,path]=floydf(E);
% 构建奇点间二分图
BinV=inf*ones(length(p),length(p));
for i=1:length(p)
for j=1:length(p)
if i~=j
BinV(i,j)=D(p(i),p(j));
end
end
end
% 令无穷大权值为 9999
BinV(BinV==inf)=9999;
LL=length(BinV);
solution=[];
% 整数规划求解最小权匹配
LL=length(BinV);
Aeq=[];
for i=1:LL
Aeq=[Aeq;zeros(1,(i-1)*LL) ones(1,LL) zeros(1,(LL-i)*LL)];
end
for i=1:LL
temp=[zeros(i-1,LL);ones(1,LL);zeros(LL-i,LL)];
temp=reshape(temp,[1,LL*LL]);
Aeq=[Aeq;temp];
end
beq=ones(2*LL,1);
for i=1:LL
for j=i+1:LL
tt=zeros(LL,LL);
tt(i,j)=1;tt(j,i)=-1;
tt=reshape(tt,[1,LL*LL]);
Aeq=[Aeq;tt];
beq=[beq;0];
end
end
lb=zeros(LL*LL,1);ub=ones(LL*LL,1);
options = optimoptions('intlinprog');
options.TolInteger=0.001;
[x,fval]=intlinprog(BinV(:),LL*LL,[],[],Aeq,beq,lb,ub,options);
x=reshape(x,[LL,LL]);
for i=1:LL
for j=i+1:LL
if x(i,j)==1;
solution=[solution;p(i) p(j)];
end
end
end
kp=x;kp(x~=0 & x~=1)=0;
kkp=find(sum(kp)==0);
p=p(kkp);
for i=1:2:length(p)
solution=[solution;p(i) p(i+1)] ;
end
% 构造配对奇点矩阵
linked=solution;
% 新增路径总权值
F=fval/2;
% 配对奇点最短路
[m,n]=size(linked);
PA(1).path=[];
for i=1:m
temp=[linked(i,1)];
while(temp(end)~=linked(i,2))
temp=[temp path(temp(end),linked(i,2))];
end
PA(i).path=temp;
end
3.2 f l e u r y fleury fleury算法的实现
1) f l e u r y fleury fleury算法
function route=fleury(E,start)
%---------------
% E 为图中各点之间的边数
% start 为起始点
%---------------
% route 为欧拉环游
%---------------
% 找到与起始点相连的点
p=find(E(start,:));
route=[start];
% 迭代求解
while(~isempty(p))
for i=1:length(p)
% 新选中边是否是桥,是桥则跳过该边
if(isBridge(route(end),p(i),E) && length(p)~=1)
continue;
else
% 更新图,走过的边导致前一端点度数-1
E(route(end),p(i))= E(route(end),p(i))-1;
% E(p(i),route(end))= E(p(i),route(end))-1; %无向图需去掉该句的注释
% 更新路线
route=[route p(i)];
% 寻找与当前点相连的点
p=find(E(route(end),:));
break;
end
end
% 若仅能寻找到起始点,且此时起始点的度数仅为 1,则找到欧拉环游
if sum(E(start,:))==1 & p==start
route=[route start];
return;
end
end
end
2)桥的判断
function flag=isBridge(startpoint,endpoint,Ete)
p=find(sum(Ete)==0);
r=find(sum(Ete')==0);
Ete(startpoint,endpoint)=Ete(startpoint,endpoint)-1;
% Ete(endpoint,startpoint)=Ete(endpoint,startpoint)-1;
q=find(sum(Ete)==0);
pdiff=setdiff(q,[p startpoint]);
pdiff=intersect(pdiff',r','rows');
if isempty(pdiff)
flag=0;
else
flag=1;
end
U=union(p,q);
U=intersect(U',r','rows');
for i=length(U):-1:1
Ete(U(i),:)=[];
Ete(:,U(i))=[];
end
Ete(Ete>=1)=1;
Q=zeros(size(Ete));
for i=1:length(Ete)
for j=1:length(Ete)
Q(i,j)=(Ete(i,j)||Ete(j,i));
end
end
[Branches,numBranch]=Net_Branches(double(Q));
if numBranch>1
flag=1;
end
end
3)连通图判断
function [Branches,numBranch]=Net_Branches(ConnectMatrix)
%---------------------------------------------------
% ConnectMatrix 为邻接矩阵(0-1)
%---------------------------------------------------
% Branches 为划分的连通图
% numBranch 图中联通子图的个数
%---------------------------------------------------
[numNode,I] = size(ConnectMatrix);
Node = [1:numNode];
Branches = [];
while any(Node)
Quence = find(Node,1);
subField=[];
while ~isempty(Quence)
currentNode = Quence(1);
Quence(1) = [];
subField=[subField,currentNode];
Node(currentNode)=0;
neighborNode=find(ConnectMatrix(currentNode,:));
for i=neighborNode
if Node(i) ~= 0
Quence=[Quence,i];
Node(i)=0;
end
end
end
subField = [subField,zeros(1,numNode-length(subField))];
Branches = [Branches;subField];
end
numBranch = size(Branches,1);
四、广义中国邮递员问题
4.1 广义中国邮递员问题的介绍
经典的中国邮递员问题是旨在找到单个邮递员在其管辖范围内完成对所有道路一次遍历的最优方案,而现实生活中一个邮局通常不止一个邮递员,而是多个邮递员同时派件,为研究更一般化的情况,本文提出广义中国邮递员问题。
定义 3 广义中国邮递员问题
多个邮递员从邮局出发,同时进行派件,要走完管辖范围内的每一条街道至少一次再返回邮局,如何选择合理的派件路线,使得最终的完成时间最短?
由如上定义可知,广义中国邮递员问题要求多人同时对道路进行遍历,需要求出使得完成任务时间最短的方案。
由于前文已对经典的中国邮递员问题做了详细的研究并且完美解决,故考虑将广义的中国邮递员问题通过某种方法转化为多个经典的中国邮递员问题,以便将前文所述的对经典的中国邮递员问题的解决方案使用在广义的中国邮递员问题中。
综上所述,若想解决广义中国邮递员问题,只需要找到一种方法将广义的中国邮递员问题化为多个经典中国邮递员问题,再对多个经典中国邮递员问题进行求解即可。
4.2 图的划分策略
根据图论相关知识,对一联通图的所有边进行恰当的选择(可重复选),可以分为若干个欧拉子图。将其运用至广义中国邮递员问题,将邮局的管辖区域分为若干块,每块分配给不同的邮递员,则转化至多个经典的中国邮递员问题,下对图的划分策略进行研究。
设 G = ( V , E ) G=(V,E) G=(V,E)为一联通图,对其所有边选择出 k k k个集合,以得到 k k k个欧拉子图 G 1 = ( V 1 , E 1 ) , G 2 = ( V 2 , E 2 ) , ⋯ , G k = ( V k , E k ) G_1=(V_1,E_1),G_2=(V_2,E_2),\cdots,G_k=(V_k,E_k) G1=(V1,E1),G2=(V2,E2),⋯,Gk=(Vk,Ek),且保证其中边权值最大的欧拉子图的总边权值取到最小值,并且这 k k k个子集的并集为 E E E。还需要保证每一个欧拉子图中都含有顶点 v 0 v_0 v0,其含义由具体情境决定,在中国邮递员问题中的可理解为邮局所在位置。
根据描述,可建立数学规划模型将图 G G G划分为多个欧拉子图,模型如下:
m i n m a x ( ∑ e ∈ E i w ( e ) ) min\ \ max(\sum_{e\in E_i}w(e)) min max(e∈Ei∑w(e)) s . t . { ⋃ i = 1 k E i = E v 0 ∈ V i , i = 1 , 2 , . . . , k G i 是 欧 拉 图 , i = 1 , 2 , . . . , k s.t.\begin{cases} \bigcup_{i=1}^kE_i=E\\ v_0\in V_i, &i=1,2,...,k\\ G_i\text是欧拉图,&i=1,2,...,k \end{cases} s.t.⎩⎪⎨⎪⎧⋃i=1kEi=Ev0∈Vi,Gi是欧拉图,i=1,2,...,ki=1,2,...,k
4.3 模型可解化
上一小节给出了一个抽象化、集合化的模型,在机理上说明了广义的中国邮递员问题可以转化为多个经典的邮递员问题,但是在计算机软件中上述模型的约束条件表达是较为困难的,所以为了对问题进行求解,必须给出一个可解的模型。
1)针对无向图
在上述模型的基础上,设原图的关联矩阵为 I ( n × m ) I_{(n\times m)} I(n×m),表明了原图中各个顶点与各条边是否关联的关系,其中 n n n与 m m m分别表示顶点与边的个数。
设欧拉子图 G i G_i Gi中使用原图中边 e j e_j ej的次数为 x i j ( i = 1 , 2 , ⋯ , k ; j = 1 , 2 , ⋯ , m ) x_{ij}(i=1,2,\cdots,k;j=1,2,\cdots ,m) xij(i=1,2,⋯,k;j=1,2,⋯,m),由此将原模型转化为
m i n m a x ( ∑ j = 1 m x i j w ( e j ) ) min\ \ max(\sum_{j=1}^mx_{ij}w(e_j)) min max(j=1∑mxijw(ej)) s . t . { ∑ i = 1 k x i j ≥ 1 , j = 1 , 2 , ⋯ , m ∑ j = 1 n x i j I v 0 j ≥ 1 , i = 1 , 2 , ⋯ , k ∑ p = 1 n ∑ j ∗ ≠ j x i j ∗ I p j I p j ∗ ≥ { 1 , x i j = 1 0 , x i j = 0 , i = 1 , 2 , ⋯ , k x i j ∈ N , i = 1 , 2 , ⋯ , k ; j = 1 , 2 , ⋯ , n s.t.\begin{cases} \sum_{i=1}^kx_{ij}\ge 1,&j=1,2,\cdots ,m\\ \sum_{j=1}^nx_{ij}I_{v_0j}\ge 1,&i=1,2,\cdots ,k\\ \sum_{p=1}^n\sum_{j^*\ne j} x_{ij^*}I_{pj}I{pj^*}\ge \begin{cases} 1,&x_{ij}=1\\ 0,&x_{ij}=0\end{cases},&i=1,2,\cdots ,k\\ x_{ij}\in N,&i=1,2,\cdots,k;j=1,2,\cdots ,n \end{cases} s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∑i=1kxij≥1,∑j=1nxijIv0j≥1,∑p=1n∑j∗̸=jxij∗IpjIpj∗≥{1,0,xij=1xij=0,xij∈N,j=1,2,⋯,mi=1,2,⋯,ki=1,2,⋯,ki=1,2,⋯,k;j=1,2,⋯,n
该模型是一个矩阵化的模型,已可利用数学软件进行求解,解得的最优解即为 k k k个子图,但这k个子图是否为欧拉图还不确定,故需要再使用最小权匹配法得到 k k k个欧拉子图,再对这 k k k个欧拉子图分别使用 f l e u r y fleury fleury算法求取欧拉回路,即可得出广义中国邮递员问题的解。
2) 针对有向图
上一个模型针对的是无向图,无向图的关联矩阵中0表示点与边无关联,1表示点与边有关联。但是有向图的关联矩阵不同,其中0已然表示无关联,用1表示边从该点出发,-1表示边进入该点。
改变无向图的模型,使得其可以应对有向图:
m i n m a x ( ∑ j = 1 m x i j w ( e j ) ) min\ \ max(\sum_{j=1}^mx_{ij}w(e_j)) min max(j=1∑mxijw(ej)) s . t . { ∑ i = 1 k x i j ≥ 1 , j = 1 , 2 , ⋯ , m Π j = 1 n x i j I v 0 j = − 1 , i = 1 , 2 , ⋯ , k ∑ p = 1 n ∑ j ∗ ≠ j ∣ x i j ∗ I p j I p j ∗ ∣ ≥ { 1 , x i j = 1 0 , x i j = 0 , i = 1 , 2 , ⋯ , k x i j ∈ N , i = 1 , 2 , ⋯ , k ; j = 1 , 2 , ⋯ , n s.t.\begin{cases} \sum_{i=1}^kx_{ij}\ge 1,&j=1,2,\cdots ,m\\ \Pi_{j=1}^nx_{ij}I_{v_0j}=- 1,&i=1,2,\cdots ,k\\ \sum_{p=1}^n\sum_{j^*\ne j} |x_{ij^*}I_{pj}I{pj^*}|\ge \begin{cases} 1,&x_{ij}=1\\ 0,&x_{ij}=0\end{cases},&i=1,2,\cdots ,k\\ x_{ij}\in N,&i=1,2,\cdots,k;j=1,2,\cdots ,n \end{cases} s.t.⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧∑i=1kxij≥1,Πj=1nxijIv0j=−1,∑p=1n∑j∗̸=j∣xij∗IpjIpj∗∣≥{1,0,xij=1xij=0,xij∈N,j=1,2,⋯,mi=1,2,⋯,ki=1,2,⋯,ki=1,2,⋯,k;j=1,2,⋯,n
4.4 公平性拓展
在实际生活工作中,大多数场合都需要保证公平性。而对于中国邮递员问题也需要考虑公平性,即每个邮递员的工作量相当,也就是说分配给每个人的道路长度应该尽量接近。
最容易联想到的就是概率论中的方差、标准差以及变异系数都是用来表示数据的离散程度的。而该问题中数据的量纲相同,故无需使用变异系数,且为保证量纲单位的次数一致,本文选用标准差来衡量公平性。
由于标准差越小表明数据的离散程度越小,即公平性越高,而模型的原目标函数也是最小化的,故可直接线性加权得到新的目标函数,即:
m i n w 1 m a x [ ∑ j = 1 m x i j w ( e j ) ] + w 2 s t d [ ∑ j = 1 m x i j w ( e j ) ] min\ w_1max[\sum_{j=1}^mx_{ij}w(e_j)]+w_2std[\sum_{j=1}^mx_{ij}w(e_j)] min w1max[j=1∑mxijw(ej)]+w2std[j=1∑mxijw(ej)]
调整 w 1 : w 2 w_1:w_2 w1:w2的数值以调整效率性与公平性的重要程度。
亦可对两目标函数进行归一化后再进行加权,但此处的归一化难度较高,有兴趣者可以自行研究。
五、广义中国邮递员问题的实践
5.1 图的划分算法
根据前文的推导,广义中国邮递员问题与经典中国邮递员问题的解法仅仅多出了图的划分部分,故仅需要再设计图的划分算法即可。
由于MATLAB2014a的整数规划模块较不完善,故建议针对具体问题使用LINGO软件求解,可直接参照第四章的模型转变为LINGO代码,再将规划结果导出,利用 f l e u r y fleury fleury算法求出各个子图的欧拉回路。
这一部分内容较为简单,且需要针对具体问题具体编程。
5.2 题目实例
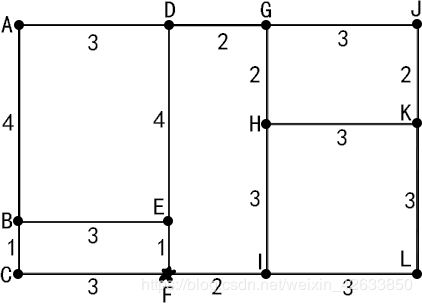
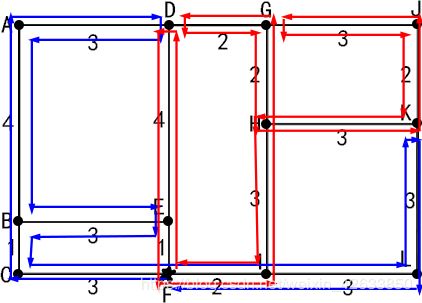
如上图,点F是邮局所在地点,该邮局有两名邮递员同时可进行派件,假设两名邮递员能力一致,尝试给出合理的派件路线(每条道路需来回各送一次)。
(1)由于每条道路需来回送两次,这样的图必为欧拉图,所以我们无需考虑生成欧拉图的部分,直接对图进行划分。首先根据图,给出图的边权矩阵,并注意到其中邮局是第六个点。
bq =
[ 1 2 4
1 4 3
2 3 1
2 5 3
3 6 3
4 5 4
4 7 2
5 6 1
6 9 2
7 8 2
7 10 3
8 9 3
8 11 3
9 12 3
10 11 2
11 12 3]
(2)根据前文的模型,若想进行图的分割,需要用到的是图关联矩阵,故执行下述代码,将边权矩阵转换为关联矩阵。
Inci=zeros(12,length(bq));
We=zeros(length(bq),1);
for i=1:length(bq)
Inci(bq(i,1),i)=1;
Inci(bq(i,2),i)=1;
We(i)=bq(i,3);
end
得到关联矩阵以及对应的边权值
Inci =
1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0
0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0
0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1
We =
4
3
1
3
3
4
2
1
2
2
3
3
3
3
2
3
(3)本题中两个矩阵规模较小,但有些实际应用问题中矩阵的规模较大,故最好将这两个文件导出,以便在LINGO中使用。
[vL,eL]=size(Inci);
file1=fopen('Incidence.txt','wt');
for i=1:vL
for j=1:eL
if j==eL
fprintf(file1,'%d\n',Inci(i,j));
else
fprintf(file1,'%d ',Inci(i,j));
end
end
end
fclose(file1);
file2=fopen('We.txt','wt');
fprintf(file2,'%f\n',We);
fclose(file2);
(4)使用LINGO软件进行规划求解,得到图的划分策略。将以下代码储存在与上述导出的文件同一目录下,并进行求解,得到图的划分策略
由于在LINGO软件中定义欧拉图较为困难,故我们可在LINGO中先得到最优子图,再在MATLAB中将图处理为欧拉图,这样至少可得到一个局部最优解。
sets:
Postman/1,2/;
Edge/1..16/:w;
Vertex/1..12/;
LinkVE(Vertex,Edge):In;
LinkCE(Postman,Edge):x;
endsets
min=@max(Postman(i):@sum(Edge(j):x(i,j)*w(j)));
@for(Postman(i):@sum(Edge(j):In(6,j)*x(i,j))>1);
@for(LinkCE:@gin(x));
@for(Edge(j):@sum(Postman(i):x(i,j))=1);
@for(Postman(i):@for(Edge(j1):@sum(Edge(j2)|(j2#ne#j1):@sum(Vertex(p):x(i,j2)*In(p,j1)*In(p,j2)))>=@if(x(i,j1)#eq#1,1,0)));
data:
In=@file('Inci.txt');
w=@file('We.txt');
enddata
解得图的划分策略
S=[0 0 0 0 0 1 1 1 1 1 1 1 1 0 1 0
1 1 1 1 1 0 0 0 0 0 0 0 0 1 0 1];
(5)下一步可以开始进行两个普通邮递员问题的求解,首先需要得到邻接矩阵
p1=find(S(1,:)==1);
p2=find(S(2,:)==1);
bq1=bq(p1,:);bq2=bq(p2,:);
[E1,o1]=bq2Adja(bq1);
[E2,o2]=bq2Adja(bq2);
其中bq2Adja函数如下:
function [Adja,porder]=bq2Adja(bq)
[p,q]=size(bq);
porder=union(bq(:,1),bq(:,2));
pA=length(porder);
Adja=inf*ones(pA,pA);
for i=1:p
k1=find(porder==bq(i,1));k2=find(porder==bq(i,2));
Adja(k1,k2)=bq(i,3);
Adja(k2,k1)=bq(i,3);
end
for i=1:pA
Adja(i,i)=0;
end
end
得出的两个邻接矩阵如下:
E1 =
0 4 Inf 3 Inf Inf Inf Inf Inf
4 0 Inf Inf Inf Inf Inf Inf Inf
Inf Inf 0 Inf Inf 3 Inf Inf Inf
3 Inf Inf 0 4 Inf 2 Inf Inf
Inf Inf Inf 4 0 Inf Inf Inf Inf
Inf Inf 3 Inf Inf 0 Inf Inf Inf
Inf Inf Inf 2 Inf Inf 0 2 Inf
Inf Inf Inf Inf Inf Inf 2 Inf 3
Inf Inf Inf Inf Inf Inf Inf 3 Inf
E2 =
0 1 3 Inf Inf Inf Inf Inf Inf Inf
1 0 Inf Inf Inf Inf Inf Inf Inf Inf
3 Inf 0 1 Inf Inf Inf Inf Inf Inf
Inf Inf 1 0 Inf Inf 2 Inf Inf Inf
Inf Inf Inf Inf 0 Inf Inf 3 Inf Inf
Inf Inf Inf Inf Inf 0 3 Inf Inf Inf
Inf Inf Inf 2 Inf 3 0 Inf Inf 3
Inf Inf Inf Inf 3 Inf Inf 0 2 Inf
Inf Inf Inf Inf Inf Inf Inf 2 0 3
Inf Inf Inf Inf Inf Inf 3 Inf 3 Inf
需要注意的是,E1中的邮局点是第六个,E2中的邮局点是第四个,可从o1,o2中看出
o1 =
1
2
3
4
5
6
7
8
11
o2 =
2
3
5
6
7
8
9
10
11
12
同时需要给出邻接矩阵的0-1形式,以便于运算。
Adja1=(E1>0 & E1<inf);Adja1=double(Adja1);
Adja2=(E2>0 & E2<inf);Adja2=double(Adja2);
(6)图的连通性检验及补全,由于LINGO对于图的连通性较难实现,故在LINGO中求出的最优解有可能不联通,故对其进行检验及补全。
首先需要对原图作 f l o y d floyd floyd算法得到最短路矩阵。
Adja=bq2Adja(bq);
D=floydf(Adja);
其中 f l o y d floyd floyd算法在正文中已给出,接下来对两个解作连通性检验。
Adja1=ToBranch(Adja1,o1,D);
Adja2=ToBranch(Adja2,o2,D);
连通性检验函数如下:
function E=ToBranch(Adja,o,D)
[Branches,numBranches]=Net_Branches(Adja);
[n,l]=size(Branches);
minD=zeros(n,n);
S(1).p=[];
for i=1:n
temp=Branches(i,:);
temp(temp==0)=[];
S(i).p= temp;
end
if length(S)==1
E=Adja;
return
end
for i=1:n
for j=1:n
if(j==i)
minD(i,j)=9999;
continue;
end
[m,order1]=min(D(o(S(i).p),o(S(j).p)));
[n,order2]=min(m);
S(i).minP=[S(i).p(order1(order2)),S(j).p(order2)];
minD(i,j)=n;
end
end
set=[];
for i=1:n-1
for j=i+1:n
set=[set;i j];
end
end
% 门特卡罗算法
minDD=1000;
for i=1:1000
ss=0;
p=randperm(n*(n-1)/2);
test=set(p,:);
t=test(:);
temp=(unique(t')~=(1:n));
if any(temp)
break;
end
for j=1:length(p)
ss=ss+minD(set(p,1),set(p,2));
end
if(ss<minDD)
minDD=ss;
minSet=set;
end
end
[l,r]=size(set);
for i=1:l
Adja(S(set(i,1)).minP(1),S(set(i,1)).minP(2))=1;
Adja(S(set(i,1)).minP(2),S(set(i,1)).minP(1))=1;
end
E=Adja;
该函数是基于蒙特卡洛随机方法的,有兴趣的读者可以考虑使用更加合理的方法,但在数据量不大的情况下,该方法已经足够。
(7)对连通性检验后的邻接矩阵作 f l e u r y fleury fleury算法,并输出路线图
route1=fleury(Adja1,find(o1==6));
route2=fleury(Adja2,find(o2==6));
L1=o1(route1);L2=o2(route2);
输出两组解:
L1 =
6
5
4
5
6
9
8
7
4
7
8
11
10
7
10
11
8
9
6
L2 =
6
3
2
1
4
1
2
5
2
3
6
9
12
11
12
9
6
(8)计算两条路线的路程,绘制出派件路线
distance1=0;
for i=1:length(L1)-1
distance1=distance1+D(L1(i),L1(i+1));
end
distance2=0;
for i=1:length(L2)-1
distance2=distance2+D(L2(i),L2(i+1));
end
输出两个邮递员各自的路程
distance1 =
44
distance2 =
44
管梅谷. 奇偶点图上作业法[J]. 数学学报,1960(3):263-266. ↩︎
郭心月. 运筹学(第四版)[M]. 清华大学出版社,2012. ↩︎