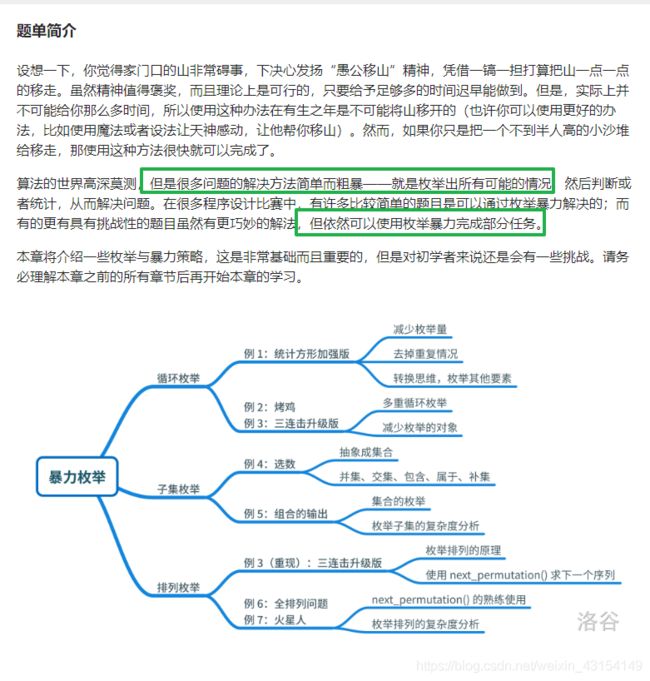
【算法1-3】暴力枚举

前言

P2241 统计方形（数据加强版）(数论，枚举，暴力)

网格中所有矩形的数量：nm(n+1)(m+1)/4
正方形的数量：for(int i=0;i

#include 

using namespace std;

typedef long long LL;

int main()
{
    LL n,m;
    cin >> n >> m;
    
    LL res = 0;
    for(int i=0;i<min(n,m);i++)
    {                       // 爆int
        res+= (m-i) * (n-i); // 边长为1的正方形为n*m个，边长为2有(n-1)*(m-1)...边长为min{n,m}有1个
    }
    
    LL sum = m * n * (m+1) * (n+1) /4; // 网格中所有矩形的数量
    
    cout<<res<<" "<<sum - res<<endl; // 所有-正方形 = 长方形的数量
    
    return 0;
}

P2089 烤鸡 (枚举）

直接十重循环枚举，时间复杂度：$3^{10}=59049$

#include 
#include 
#include 

using namespace std;

vector<vector<int> > nums;
vector<int> num;

int main()
{
    
    int n;
    cin>>n;
    
    int k=0;
    int res=0;
    for(int a=1;a<=3;a++)
    for(int b=1;b<=3;b++)
    for(int c=1;c<=3;c++)
    for(int d=1;d<=3;d++)
    for(int e=1;e<=3;e++)
    for(int f=1;f<=3;f++)
    for(int g=1;g<=3;g++)
    for(int h=1;h<=3;h++)
    for(int i=1;i<=3;i++)
    for(int j=1;j<=3;j++)
    {
        if(a+b+c+d+e+f+g+h+i+j == n) {
            num.clear();
            res++;
            num.push_back(a);
            num.push_back(b);
            num.push_back(c);
            num.push_back(d);
            num.push_back(e);
            num.push_back(f);
            num.push_back(g);
            num.push_back(h);
            num.push_back(i);
            num.push_back(j);
            
            nums.push_back(num);
        }
    }
    
    printf("%d\n",res);
    for(int i =0;i<nums.size();i++){
        for(int j=0;j<nums[i].size();j++) printf("%d ",nums[i][j]);
        printf("\n");
    }
    
    
    return 0;
}

P1618 三连击（升级版）(枚举)

直接从100~999范围里枚举第一个数，根据输入生成其他数，再判定是否符合题意(这也是非常常用的转换思路的方法)。
st[] 判断9个数是否都出现过

#include 
#include 
#include 
#include 

using namespace std;

const int N = 10;

bool st[N];

int main()
{
    double a,b,c;
    //cin>>a>>b>>c;
    scanf("%lf%lf%lf",&a,&b,&c);
    
    int flag=false;
    for(int i=123;i<=987;i++)
    {
        memset(st,0,sizeof st);
        int i2= i * (b/a), i3 = i * (c/a);
        if(i2 < 123 || i2 > 987 || i3 < 123 || i3 > 987) break;

        
        st[i%10]=st[i/10%10]=st[i/100]=true; // i%10 取个位，i/10%10 取十位 i/100 取百位
        st[i2%10]=st[i2/10%10]=st[i2/100]=true;
        st[i3%10]=st[i3/10%10]=st[i3/100]=true;
        
        int v=0;
        for(int i = 1;i<=9;i++) v+=st[i];
        if(v==9){
            int t[3]={i,i2,i3};
            sort(t,t+3);
            printf("%d %d %d\n",t[0],t[1],t[2]);
            flag=true;
        }
    }
    
    if(!flag) printf("No!!!");
    
    return 0;
}

P1036 选数(dfs)

dfs搜索，dfs函数最重要的就是参数（要什么填什么）

#include 

using namespace std;

const int N = 22;

int n,k;
int a[N];
int ans; // dfs全局答案

bool isprime(int x) // 试除法求素数，O(logn)
{
    for(int i=2;i<=x/i;i++)
        if(x % i == 0) return false;
    return true;
}

void dfs(int m,int sum,int start) // m:当前选了多少个数,sum:总和,start:表示升序排列，以免算重
{
    if(m == k)
    {
        if(isprime(sum)) ans ++;
        return ;
    }    
    
    for(int i=start;i<n;i++)
        dfs(m+1,sum + a[i],i+1);
    
}

int main()
{
    cin >> n >> k;
    
    for(int i=0;i<n;i++) cin >> a[i];
    
    dfs(0,0,0);
    
    cout<<ans<<endl;
    
    return 0;
}

P1157 组合的输出(递归实现组合型枚举)(dfs)

避免重复可以人为地定顺序
剪枝会快3倍
此外，给出递归实现指数型枚举和排列型枚举

#include 
#include 

using namespace std;

const int N =25;

int n,k;
int st[N]; // 当前位置填哪个数

void dfs(int u,int start) // u:当前位置，start:下一个数开始
{
    if(u + n - start < k) return; // 剪枝
    if(u > k)
    {
        for(int i=1;i<=k;i++) printf("%3d",st[i]);
        cout<<endl;
        return;
    }
    
    for(int i=start;i<=n;i++) // 人为升序，避免重复
    {
        st[u] = i;
        dfs(u+1,i+1);
        st[u] = 0;
    }
}

int main()
{
    cin >> n >> k;
    dfs(1,1);
    
    return 0;
}

递归实现指数型枚举

#递归最重要的在于递归顺序
#递归思路 ： 1.边界 2.递归 3.恢复现场
##数据结构：int st[N];//记录每个位置当前的状态：0还没考虑，1表示选它，2表示不选它

#include 
#include 
#include 
#include 

using namespace std;

const int N = 16;

int n;
int st[N];//记录每个位置当前的状态：0还没考虑，1表示选它，2表示不选它

//递归思路 ： 1.边界 2.递归 3.恢复现场
void dfs(int u)
{
    if(u>n)  //边界
    {
        for(int i=1;i<=n;i++) 
        {
            if(st[i]==1) printf("%d ",i);
        }
        puts("");
        return ;
    }
    
    st[u]=2;    
    dfs(u+1);   //递归
    st[u]=0;    //恢复现场
    
    st[u]=1;
    dfs(u+1);
    st[u]=0;
        
}

int main()
{
    cin>>n;
    
    dfs(1);
    
    return 0;
}

##记录方案实现：

#include 
#include 
#include 
#include 
#include 

using namespace std;

const int N = 16;

int n;
int st[N];//记录每个位置当前的状态：0还没考虑，1表示选它，2表示不选它
vector<vector<int>> ways;

//递归思路 ： 1.边界 2.递归 3.恢复现场
void dfs(int u)
{
    if(u>n)  //边界
    {
        vector<int> way;
        for(int i=1;i<=n;i++) 
        {
            if(st[i]==1) way.push_back(i);
        }
        ways.push_back(way);
        return ;
    }
    
    st[u]=2;    
    dfs(u+1);   //递归
    st[u]=0;    //恢复现场
    
    st[u]=1;
    dfs(u+1);
    st[u]=0;
        
}

int main()
{
    cin>>n;
    
    dfs(1);
    
    for(int i=0;i<ways.size();i++)
    {
        for(int j=0;j<ways[i].size();j++) printf("%d ",ways[i][j]);
        printf("\n");
    }
        
    
    return 0;
}

递归实现排列型枚举

数据结构：int st[N]; bool used[N];

#include 

using namespace std;

const int N = 10;

int n;
int st[N];  // 当前位上填哪个数
bool used[N]; // 数是否用过

//递归顺序：每一位上有哪个数可用
void dfs(int u)
{
    if(u>n)
    {
        for(int i=1;i<=n;i++)
        {
            printf("%d ",st[i]);
        }
        puts("");
        return ;
    }
    
    //依次枚举当前哪个数可用
    for(int i=1;i<=n;i++)
    {
        if(!used[i])
        {
            st[u]=i;
            used[i]=true;
            dfs(u+1);
            
            //恢复现场
            st[u]=0;
            used[i]=false;
        }
    }
    
}

int main()
{
    cin>>n;
    
    dfs(1);
    
    return 0;
}

递归实现组合型枚举

##避免重复可以人为地定顺序
##剪枝会快3倍

#include 
#include 
#include 
#include 

using namespace std;

const int N = 30;

int n,m;
int way[N];

void dfs(int u,int start)
{
    if(u+n-start<m) return ; //剪枝
    if(u>m) //边界
    {
        for(int i=1;i<=m;i++) printf("%d ",way[i]);
        puts("");
        return ;
    }
    
    for(int i=start;i<=n;i++)
    {
        way[u]=i;
        dfs(u+1,i+1);   //递归
        way[u]=0;   //恢复现场
    }
}

int main()
{
    cin>>n>>m;
    
    dfs(1,1);//参数：当前枚举哪个位置u ，当前最小可以从哪个数枚举
    
    return 0;
}

P1706 全排列问题(dfs)

递归实现排列型（略）
此外，运用库文件 里的next_permutation() 函数求下一个序列

#include 
#include 
#include 

using namespace std;

const int N = 10;

int a[N];

int main()
{
    int n;
    cin >> n;
    for(int i=0;i<n;i++) a[i] = i+1;
    
    do{
        for(int i=0;i<n;i++) printf("%5d",a[i]);
        cout<<endl;
    }while(next_permutation(a,a+n));
    
    return 0;
}

P1088 火星人(next_permutation())

求当前序列的下m个序列，熟练运用next_permutation()

#include 
#include 

using namespace std;

const int N = 100010;

int a[N];

int main()
{
    int n,m;
    cin >> n >> m;
    
    for(int i=0;i<n;i++) cin >> a[i];
    
    while(m--)
    {
        next_permutation(a,a+n);
    }
    
    for(int i=0;i<n;i++) cout<<a[i]<<" ";
    
    return 0;
}

P3392 涂国旗(枚举)

#include 

using namespace std;

const int N = 55;

int n,m;
int w[N],b[N],r[N]; // 第i行换成W的成本
char s[N][N];


int main()
{
    cin >> n >> m;
    for(int i=1;i<=n;i++) cin >> s[i]; // 下标从1开始
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<m;j++)
        {
            if(s[i][j] != 'W') w[i]++;
            if(s[i][j] != 'R') r[i]++;
            if(s[i][j] != 'B') b[i]++;
        }
    }
    
    int res=1e9;
    for(int i=1;i<=n-2;i++)
        for(int j=i+1;j<=n-1;j++)
        {
            int sum = 0;
            for(int k=1;k<=i;k++) sum += w[k];
            
            for(int k=i+1;k<=j;k++) sum += b[k];
            
            for(int k=j+1;k<=n;k++) sum += r[k];
            
            res=min(res,sum);
        }
    
    cout<<res<<endl;
    
    return 0;
    
}

P3654 First Step (ファーストステップ)(枚举)

#include 

using namespace std;

const int N = 110;

int n,m,k;
char s[N][N];

bool row(int x,int y,int k)
{
    
    for(int i=0;i<k;i++) 
        if(s[x][y+i] != '.')
        {
            return false;
        }
    return true;
}

bool col(int x,int y,int k)
{
    
    for(int i=0;i<k;i++) 
        if(s[x+i][y] != '.')
        {
            return false;
        }
    return true;
}

int main()
{
    cin >> n >> m >>k;
    
    for(int i=0;i<n;i++) cin >> s[i];
    
    int res=0;
    for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        {
            if(s[i][j]=='.') 
            {
                if(row(i,j,k)) res++;
                if(col(i,j,k)) res++;
            }
        }
        
    if(k==1) res/=2;
    cout<<res<<endl;
    
    return 0;
}

P1217 [USACO1.5]回文质数 Prime Palindromes(枚举)

学一手：

试除法求质数O(logn)
判断回文质数 (数字反转)

#include 


using namespace std;

bool isH(int x)
{
    int t=x,sum = 0;
    while(t)
    {
        sum = sum*10 + t % 10;
        t/=10;
    }
    if(sum == x) return true;
    return false;
}

bool isprime(int x)
{
    for(int i=2;i<=x/i;i++)
        if(x % i == 0) return false;
    return true;
}

int main()
{
    int a,b;
    cin >> a >> b;
    b= min(b,10000000);  // 迷之优化
    for(int i=a;i<=b;i++)
        if(isH(i) && isprime(i)) 
            cout<<i<<endl;
    //cout<
        
    return 0;
}

P1149 火柴棒等式(枚举)

#include 

using namespace std;

int a[10]={6,2,5,5,4,5,6,3,7,6}; // 0-9数字所需的火柴棒

int match(int x) // 一个数所需要的火柴棒个数
{
    int res=0;
    for(int i=x;i;i/=10) res += a[i%10];
    if(x == 0) res+=a[0];
    
    return res;
}

int main()
{
    int n;
    cin >> n;
    
    int res=0;
    
    for(int i=0;i<=1111;i++) // 估计最大1111, 1111 + 1 = 1112  25条
        for(int j=0;j<=1111;j++)
        {
            if(match(i) + match(j) + match(i+j) + 4 == n) res++;
        }
    
    cout<<res<<endl;
    
    return 0;
}

P3799 妖梦拼木棒(枚举)

#include 

using namespace std;

const int N = 5010, mod = 1E9 + 7;

typedef long long LL;

LL a[N]; // 桶

int C(int x,int k)
{
    return k==1? x : x*(x-1)/2;
}

int main()
{
    int n;
    cin >> n;
    for(int i=0;i<n;i++)
    {
        int x;
        cin >> x;
        a[x] ++;
    }
    
    // a = b = c + d;
    // 枚举a,确定c,d
    LL res=0;
    for(int i=2;i<=5000;i++)
        if(a[i] >= 2)
        {
            int times = C(a[i],2)%mod;
            for(int j=1;j<=i/2;j++)
            {
                if(j != i-j && a[j] >=1 && a[i-j] >=1)
                    res = (res + times * C(a[j],1)%mod * C(a[i-j],1)%mod ) %mod;
                else if(j==i-j && a[j] >= 2)
                    res = (res + times * C(a[j],2)%mod ) %mod;
            }
        }
    
    cout<<res<<endl;
    
}

P2392 kkksc03考前临时抱佛脚(贪心，背包)

#include 
#include 

using namespace std;

const int N = 610;

int len[5];
int s[21];
int f[N];

int main()
{
    for(int i=1;i<=4;i++) cin >> len[i];
    
    int res=0;
    for(int i=1;i<=4;i++)
    {
        int sum = 0;
        for(int j=1;j<=len[i];j++) 
        {
            cin >> s[j];
            sum += s[j];
        }
        
        // 作01背包，容量是 sum/2
        for(int j=1;j<=len[i];j++)
            for(int k=sum/2;k>=s[j];k--)
                f[k]=max(f[k],f[k-s[j]] + s[j]); // 体积和价值都是时间
        res += max(sum - f[sum/2],f[sum/2]); // 取两边较大的
        
        // f[]清0
        for(int j=1;j<=sum/2;j++) f[j]=0;
    }
    
    cout<<res<<endl;
    
    return 0;
}

P2036 Perket(dfs)

dfs暴搜，选或不选，可利用位运算枚举

代码1

#include 
#include 

using namespace std;

const int N = 15;

int n;
int ans =0x3f3f3f3f; // 记录一个全局最小答案
int a[N],b[N];

void dfs(int u,int x,int y) // u表示当前的配料编号，x为酸度，y为甜度
{
    if(u>n) 
    {
        // 清水
        if(x==1 && y==0) return;
        
        ans = min(ans,abs(x-y));
        return;
    }
    
    // 选第i个配料
    dfs(u+1,x*a[u],y+b[u]);
    // 不选
    dfs(u+1,x,y);
}

int main()
{
    cin >> n;
    for(int i=1;i<=n;i++) cin >> a[i] >> b[i];
    
    dfs(1,1,0);
    
    cout<<ans<<endl;
    
    return 0;
}

代码2(位运算枚举)

#include 
#include 

using namespace std;

const int N = 15;

int n;
int ans =0x3f3f3f3f; // 记录一个全局最小答案
int a[N],b[N];


int main()
{
    cin >> n;
    for(int i=1;i<=n;i++) cin >> a[i] >> b[i];
    
    // 位运算枚举
    for(int i=1;i<(1<<n);i++)
    {
        int sa=1,sb=0;
        for(int j=0;j<n;j++)
            if(i >> j & 1)
            {
                sa *= a[j+1];
                sb += b[j+1];
            }
        ans = min(ans,abs(sa-sb));
    }
    
    cout<<ans<<endl;
    
    return 0;
}

P1433 吃奶酪(DP，状态压缩，dfs)

还不会状态压缩（等学一手再回来做），这里给出dfs搜索代码，90分（最后一个点超时）

#include 
#include 
#include 

using namespace std;

const int N = 16;

int n;
bool vis[N]; 
double x[N],y[N];
double dist[N][N]; // dist[i][j] 表示 点i 到点j的距离（预处理）
double ans = 1e9; // 定义全局最小答案

double distance(double x1,double y1,double x2,double y2)
{
    return sqrt((x1-x2) * (x1-x2) + (y1-y2) * (y1-y2));
}

void dfs(int step,int u,double sum) // step:已走过的点 u:当前点，sum :走过的总长
{
    if(sum >= ans) return ; // 剪枝
    
    if(step == n)
    {
        ans = sum;
        return;
    }
    
    
    for(int i=1;i<=n;i++)
        if(!vis[i] && u != i)
        {
            vis[i] = true;
            dfs(step + 1,i,sum + dist[u][i]);
            vis[i] = false; // 恢复现场
        }
}

int main()
{
    cin >> n;
    for(int i=1;i<=n;i++) cin >> x[i] >> y[i];
    
    x[0] = y[0] = 0; // 设起点为第0个点
    
    for(int i=0;i<=n;i++)
        for(int j=0;j<=n;j++)
            dist[i][j] = distance(x[i],y[i],x[j],y[j]);
    
    dfs(0,0,0.0);
            
    printf("%.2lf",ans);
}