基于直方图及动态时间规整(DTW)的运动物体(透视变形)位移估计
基于直方图及动态时间规整(DTW)的运动物体(透视变形)位移估计
- 前言
- (一)获取两张图片的直方图投影
- (二)动态时间规整(Dynamic Time Wraping)
- (三)效果展示
- (四)总结
前言
对于两张图片,需要求出它们之间的运动距离,我们可以通过互相关函数、模板匹配、迭代临近点等方式来求,倘若我们想得到每个区域或每个点的相对运动,该如何去做呢?下文只从X方向来讲解,可以拓展至二维中。
(一)获取两张图片的直方图投影
首先,我们可以获取两张图片关于水平方向的直方图投影,即统计每列的像素点个数。如下:
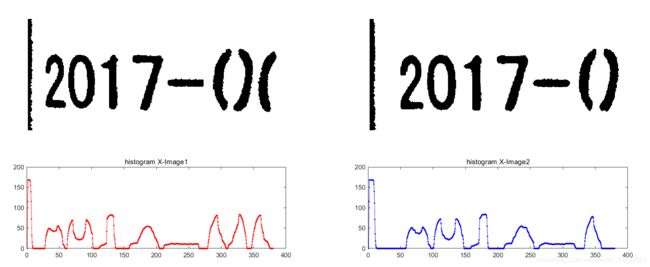
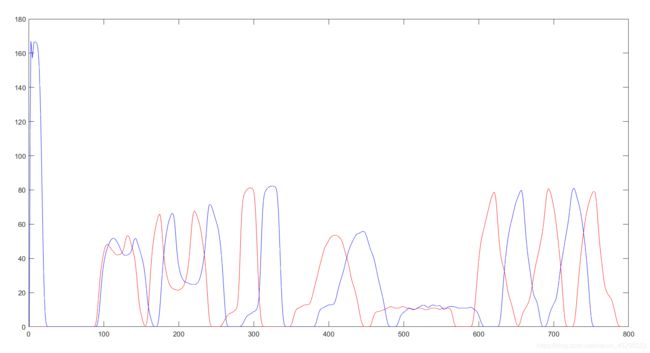
通过上图我们发现,两张图片的趋势大体相同,但是图片由于轻微的变形,使得直方图中对应字体的区间长度发生了一定的变化。我们是否可以找到一种方法来做匹配呢?
(二)动态时间规整(Dynamic Time Wraping)
DTW是通过动态时间规划思想,解决了序列匹配中长短不一的问题。具体就不介绍了。
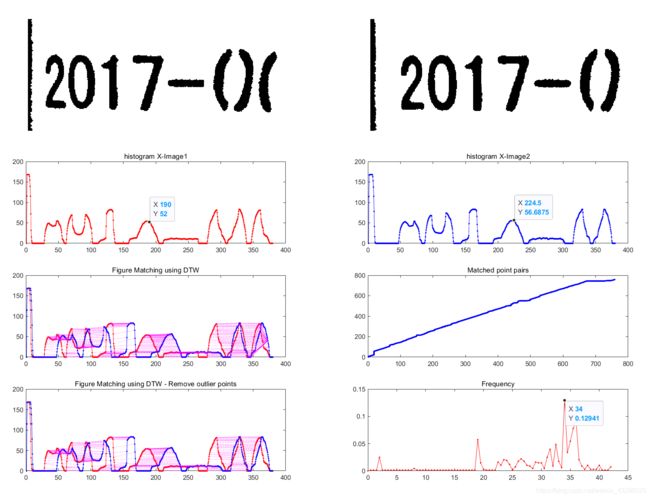
下面通过使用matlab实现两帧图片中的数字位移的求解,并取位移众数作为图片间的相对位移。具体思路如下:
- 直方图投影获取两幅图片在X方向的映射
- 滤波,可以使用高斯平滑或中值滤波
- 插值算法增加点对个数
- 动态时间规整寻找匹配点对
- 剔除一对多的情况
- 统计距离众数作为图片的相对位移。
具体Matlab代码实现如下:
close all;clc; clear
image1 = imread('./data/19.tiff');
image2 = imread('./data/22.tiff');
bwImage1 = ~imbinarize(image1(:,:,1));
bwImage2 = ~imbinarize(image2(:,:,1));
hist_X1 = sum(bwImage1)';
hist_X2 = sum(bwImage2)';
% Medium filter operation
%hist_X1 = medfilt1(hist_X1,3);
%hist_X2 = medfilt1(hist_X2,3);
hist_Y1 = sum(bwImage1,2)';
hist_Y2 = sum(bwImage2,2)';
nx = length(hist_X1); mx = length(hist_X2);
x1 = 1:0.5:(nx); x2 = 1:0.5:(mx);
xx1 = 1:(nx); xx2 = 1:mx;
hist_X1 = interp1(xx1,hist_X1,x1,'pchip');
hist_X2 = interp1(xx2,hist_X2,x2,'pchip');
ny = length(hist_Y1); my = length(hist_Y2);
y1 = 1:(ny);y2 = 1:(my);
figure(1);
subplot(3,2,1);
plot(x1,hist_X1,'r.-');
title('histogram X-Image1');
subplot(3,2,2)
plot(x2,hist_X2,'b.-');
title('histogram X-Image2');
subplot(3,2,3)
[dist, ix, iy] = dtw(hist_X1,hist_X2);
plot(x1,hist_X1,'r.-');
hold on;
plot(x2,hist_X2,'b.-');
for i= 1:length(ix)
line([x1(ix(i)),x2(iy(i))],[hist_X1(ix(i)),hist_X2(iy(i))],'color','m','linestyle',':');
end
title('Figure Matching using DTW');
hold off
subplot(3,2,4);
plot(ix,iy,'b.');
title('Matched point pairs');
% Remove one to many point pairs
tmp = tabulate(iy);
oneToMany = find(tmp(:,2,:)~=1);
ind = [];
for i = 1:length(oneToMany)
ind = [ind; find(iy == oneToMany(i))];
end
ix(ind) = [];
iy(ind) = [];
ind = [];
for i = 1:length(oneToMany)
ind = [ind; find(ix == oneToMany(i))];
end
ix(ind) = [];
iy(ind) = [];
subplot(3,2,5)
plot(x1,hist_X1,'r.-');
hold on;
plot(x2,hist_X2,'b.-');
for i= 1:length(ix)
handle = line([x1(ix(i)),x2(iy(i))],[hist_X1(ix(i)),hist_X2(iy(i))],'color','m','linestyle',':');
end
title('Figure Matching using DTW - Remove outlier points');
hold off
diffX = x2(iy)-x1(ix);
a = tabulate(diffX);
a(find(a(:,1,1)==0),:,:) = 0;
subplot(3,2,6);
plot(a(:,1),a(:,3)/100,'r.-');
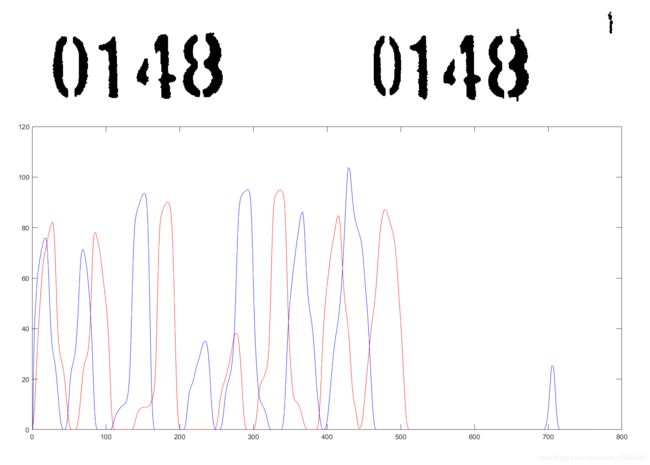
title('Frequency');(三)效果展示
(四)总结
为了更好的匹配,可以通过控制dtw函数中 c i j , c i , c j c_{ij},c_i,c_j cij,ci,cj的权值来约束边界匹配情况。在点对匹配图中(图4)如果出现斜率接近0或者接近正无穷的情况,我们可以判定该部位没有匹配成功。