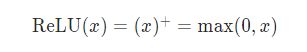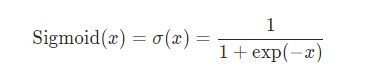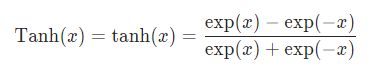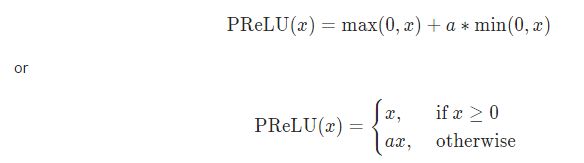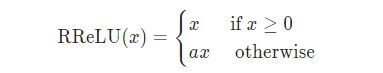深度学习中的激活函数总结以及pytorch实现

一、简介

在神经网络中，激活函数决定一个节点从一组给定输入的输出，而非线性激活函数允许网络复制复杂的非线性行为。由于大多数神经网络使用某种形式的梯度下降进行优化，激活函数必须是可微的(或者至少是几乎完全可微的)。此外，复杂的激活函数可能会产生关于渐变消失和爆炸的问题。因此，神经网络倾向于使用一些选定的激活函数(identity, sigmoid, ReLU和它们的变量)。

下面我就结合pytorch官方文档.和 这个可视化网页.来看一些常见的激活函数，这个可视化激活函数网页很形象。先附上一些常用的激活函数，以便快速查看。

二、常用激活函数

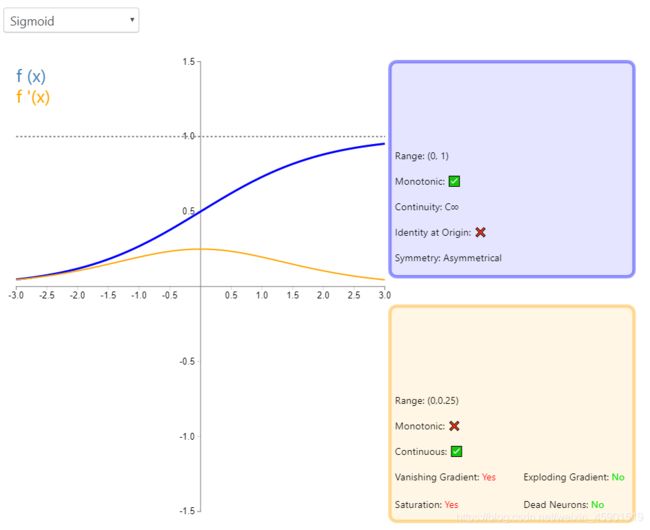
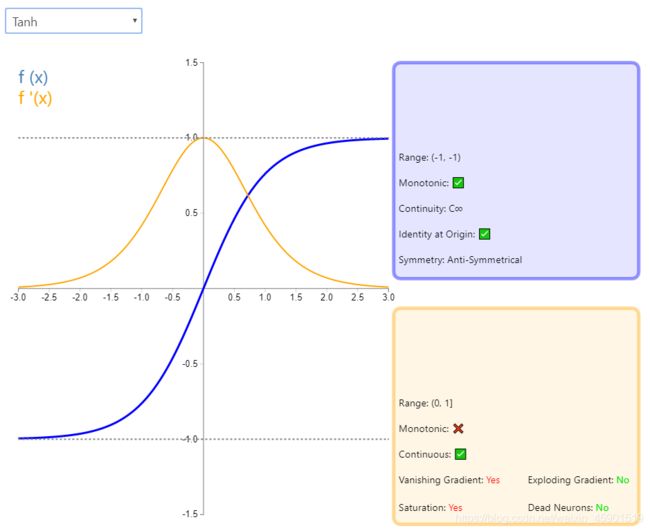
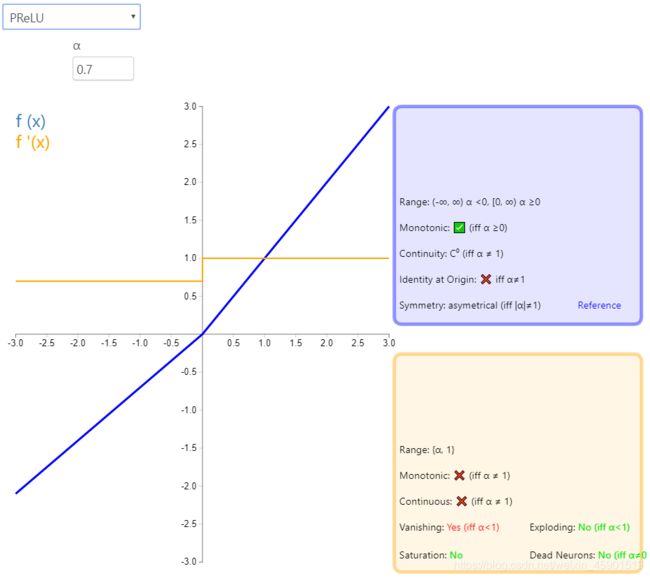
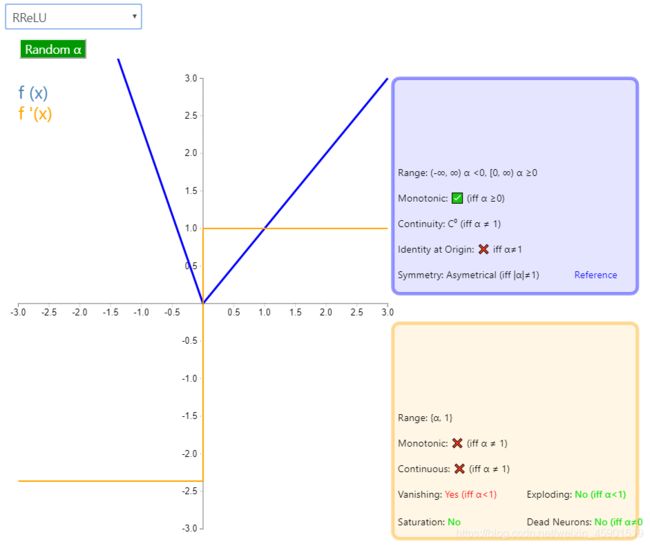
说明：图基本能说明一切，需要注意的是它的导数。pytorch中也介绍的比较详细，可查看pytorch官方文档看看参数的使用。

1、ReLU

公式：

pytorch中实现的例子：

>>> import torch
>>> import torch.nn as nn
>>> m = nn.ReLU()
>>> input = torch.randn(2)
>>> output = m(input)
>>> output
tensor([0.0000, 1.2999])

2、Sigmoid

公式：

pytorch中实现的例子：

>>> import torch
>>> import torch.nn as nn
>>> m = nn.Sigmoid()
>>> input = torch.randn(2)
>>> output = m(input)
>>> output
tensor([0.8888, 0.3325])

3、Tanh

公式：

pytorch中实现的例子：

>>> import torch
>>> import torch.nn as nn
>>> m = nn.Tanh()
>>> input = torch.randn(2)
>>> output = m(input)
>>> output
tensor([0.5014, 0.9791])

4、LeakyReLU

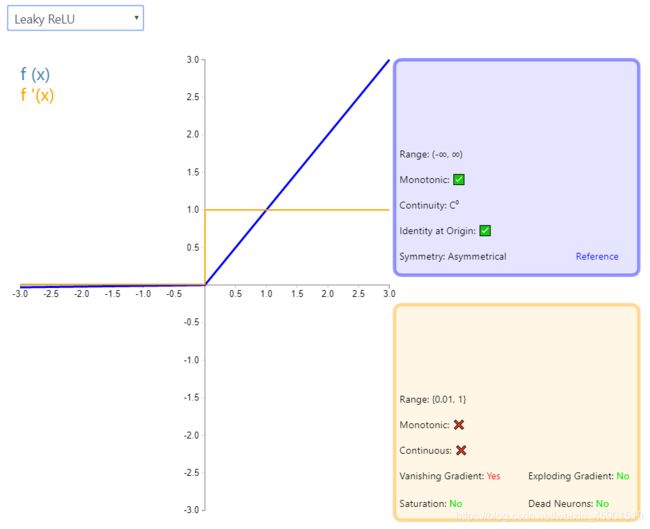
注意：LeakyReLU对负值输入有一个非常小的斜率。由于导数总是不为零，这可以减轻对死亡神经元的影响，从而允许基于梯度的学习发生(无论多慢)。

公式：

pytorch中实现的例子：

>>> import torch
>>> import torch.nn as nn
>>> m = nn.LeakyReLU(0.1)
>>> input = torch.randn(2)
>>> output = m(input)
>>> output
tensor([ 0.5794, -0.0122])

5、PReLU

公式：

pytorch中实现的例子：

>>> import torch
>>> import torch.nn as nn
>>> m = nn.PReLU()
>>> input = torch.randn(2)
>>> output = m(input)
>>> output
tensor([-0.5252, -0.2924], grad_fn=<PreluBackward>)

6、RReLU

公式：

pytorch中实现的例子：

>>> import torch
>>> import torch.nn as nn
>>> m = nn.RReLU(0.1, 0.3)
>>> input = torch.randn(2)
>>> output = m(input)
>>> output
tensor([-0.0875, -0.2063])

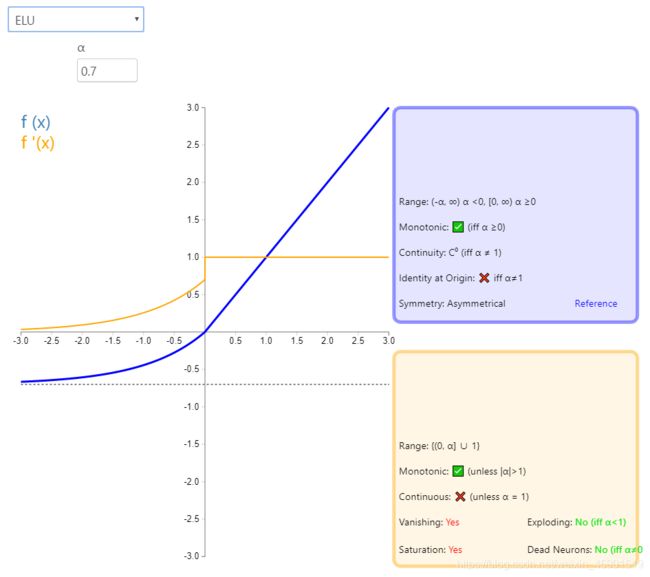
7、ELU

公式：

pytorch中实现的例子：

>>> import torch
>>> import torch.nn as nn
>>> m = nn.ELU()
>>> input = torch.randn(2)
>>> output = m(input)
>>> output
tensor([-0.0666,  0.9408])

三、参考文献

1: https://dashee87.github.io/deep%20learning/visualising-activation-functions-in-neural-networks/.

2: https://pytorch.org/docs/stable/nn.html#non-linear-activations-weighted-sum-nonlinearity.

3: http://rasbt.github.io/mlxtend/user_guide/general_concepts/activation-functions/#activation-functions-for-artificial-neural-networks.