3.通信原理——随机过程（第七版 樊昌信 曹丽娜编著）
因为第二章确知信号主要是讲频域中功率信号、能量信号和功率信号的功率谱密度，能量信号的能量谱密度，时域中能量信号和功率信号的自相关函数和和互相关函数，在其他科目中会有讲解，所以这里不再多说。第三章将随机过程，在之前科目中也有提到，所以这里就只简单介绍一下。
目录
3.1 随机过程的基本概念
3.2 平稳随机过程
3.2.1 定义
3.2.2 各态历经性
3.2.3 平稳过程中的自相关函数
3.2.4 平稳过程中的功率谱密度
3.3 高斯随机过程
3.3.1 定义
3.3.2 重要性质
3.3.3 高斯随机变量
3.4 平稳随机过程通过线性系统
3.5 窄带随机过程
3.6 正弦波加窄带高斯噪声
3.7 高斯白噪声和带限白噪声
3.7.1 白噪声
3.7.2 低通白噪声
3.7.3 带通白噪声
3.8 小结
3.1 随机过程的基本概念
随机过程是所有样本函数的集合。（样本函数是测试结果的每一个记录都是一个确定的时间函数）
随机过程也可以看成为时间进程中处于不同时刻的随机变量的集合。(随机变量以时间为参变量)
3.2 平稳随机过程
3.2.1 定义
严(狭义)平稳过程：任意n维分布与时间起点无关,而只与这n点的时间间隔有关。
宽(广义)平稳过程：不一定是严平稳过程,但具有严平稳过程的某些特征（通信中遇到的绝大部分随机过程属于这一类）。
可以由严(狭义)平稳引出宽(广义)平稳
如果一个随机过程满足下列条件则称之为“宽（或广义）平稳过程”：
（1）均值函数为常数
（2）自相关函数只与两个时间点之间的时间差τ有关，与时间起点无关
注意：严平稳随机过程必定是广义平稳的，反之不一定成立。
3.2.2 各态历经性
平稳过程的遍历性（各态历经性）：如果一个随机过程做1次实验，在时间上的统计特征等于做无数次试验的统计特征，称这种过程具有遍历性。
各态历经性的含义：无需作无线多次的考察，用一次实现的“时间平均”值代替过程的“统计平均”值即可。
注意：具有各态历经的随机过程一定是平稳过程，反之不一定。在通信系统中所遇到的随机信号和噪声，一般都能满足各态历经性。
3.2.3 平稳过程中的自相关函数
![(1) R(0)=E\left[\xi^{2}(t)\right]=S](http://img.e-com-net.com/image/info8/5535259e95ae4a37ab26f79215cc2f08.gif){kind=small}
的平均功率
![\text { (2) } R(\infty)=E^{2}[\xi(t)]](http://img.e-com-net.com/image/info8/8bb12324ae3e4d5280504be4b1b1d48a.gif){kind=small}
的直流功率
![\text { (3) } R(0)-R(\infty)=E\left[\xi^{2}(t)\right]-E^{2}[\xi(t)]=\sigma^{2}](http://img.e-com-net.com/image/info8/b227b2200e1e4905b9a7e9eee24dacd6.gif){kind=small}
的交流功率
平稳过程的自相关函数为偶函数
自相关函数是有界的
3.2.4 平稳过程中的功率谱密度
平稳过程的功率谱密度与其自相关函数是一对傅里叶变换关系。——维纳-辛钦定理
3.3 高斯随机过程
3.3.1 定义
若一随机过程的任意n维分布都是正态分布，称高斯过程。
3.3.2 重要性质
对高斯过程，严平稳等价于宽平稳。
对高斯过程，不相关等价于独立。
高斯过程通过线性系统仍为高斯过程。
3.3.3 高斯随机变量
任一时刻的取值是一个正态分布的随机变量，也称高斯随机变量， 一维概率密度函数为
，（a为均值， σ ^2为方差）
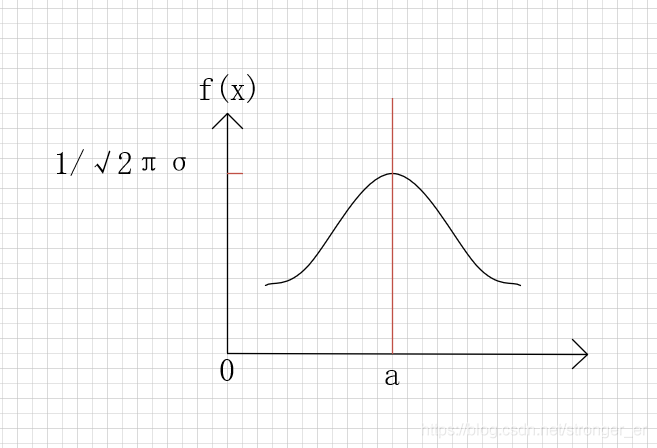
正态分布的特性（这个图画的有点很不标准，就将就着看吧）
（1） f (x)对称于直线 x = a
（2）
， 
（3） a表示分布中心， σ 表示集中程度，图形随σ 的减小，而变高和变窄。
（4）当a = 0， σ = 1时， f (x)为标准正态分布：
3.4 平稳随机过程通过线性系统
1. ![E\left[\xi_{O}(t)\right]=E\left[\xi_{i}(t)\right] \bullet H(0)](http://img.e-com-net.com/image/info8/7268a95e80314b93855f82c2c4625901.gif){kind=small}
输出过程的均值是一个常数
2. 线性系统的输入过程是平稳的，那么输出过程也是平稳的。
3. 
输出过程的功率谱密度是输入过程的功率谱密度乘以系统频率响应模值的平方。
4. 高斯过程经线性变换后的过程仍为高斯过程
3.5 窄带随机过程
窄带随机过程的表示式 ：![\xi(t)=a_{\xi}(t) \cos \left[\omega_{c} t+\varphi_{\xi}(t)\right], \quad a_{\xi}(t) \geq 0](http://img.e-com-net.com/image/info8/8a99a2835ebf477882828d552e06da0e.gif){kind=small}
可以展开为：
：的同相分量
： 的正交分量
因为ξ(t)平稳且均值为零，对于任意t，都有E[ξ(t)] = 0 ，所以![E\left[\xi_{c}(t)\right]=0, \quad E\left[\xi_{s}(t)\right]=0](http://img.e-com-net.com/image/info8/c194bfee66c548e8808b08a871a035fe.gif){kind=small}
结论：一个均值为零的窄带平稳高斯过程，同相分量ξc(t)和正交分量ξs(t)同样是平稳高斯过程，且均值为零，方差相同。同一时刻上得的ξc和ξs互不相关或统计独立。
一个均值为零，方差为
的窄带平稳高斯过程ξ(t)，包络
的一维分布是瑞利分布，相位
的一维
分布是均匀分布，与统计独立 ，即
3.6 正弦波加窄带高斯噪声
正弦波加窄带高斯噪声的包络分布与信噪比有关：小信噪比时，接近于瑞利分布
大信噪比时，接近于高斯分布
一般情况下时，莱斯分布
正弦波加窄带高斯噪声的相位分布也与信噪比有关：小信噪比时接近于均匀分布。
3.7 高斯白噪声和带限白噪声
3.7.1 白噪声
定义：功率谱密度在所有频率上均为常数的噪声
双边功率谱密度 
单边功率谱密度 
白噪声和自相关函数的曲线 
由于白噪声的带宽无限，平均功率为无穷大，即
若噪声的功率谱均匀分布的频率范围远远大于通信系统的工作频带，就视为白噪声。
白噪声取值的概率分布服从高斯分布，称高斯白噪声， 性质：
1.概率分布服从高斯分布
2.功率谱是常数
高斯白噪声在任意两个不同时刻上的随机变量之间，互不相关且统计独立
3.7.2 低通白噪声
定义：如果白噪声通过理想矩形的低通滤波器或理想低通信道，输出的噪声称低通白噪声。
功率谱密度：
自相关函数：
3.7.3 带通白噪声
若白噪声通过理想矩形的带通滤波器或理想带通信道，称带通白噪声。
带通滤波器的B << fc，称窄带滤波器，把带通白高斯噪声称窄带高斯白噪声。
窄带高斯白噪声的表达式和统计特性和窄带随机过程相同。
平均功率：
3.8 小结
1. 随机过程的数字特征（均值、方差、相关函数）；
2. 广义平稳和狭义平稳的定义及其关系；
3. 各态历经性：随机过程中的任一次实现都经历了随机过程的所有可能状态；
4. 平稳随机过程通过线性系统：若线性系统的输入过程是平稳的，那么输出过程也是平稳的； 如果线性系统的输入过程是高斯型的，则系统的输出过程也是高斯的；高斯过程经线性变换后的过程仍为高斯过程。