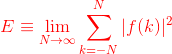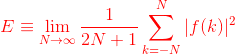stronger_er
stronger_er

信号与线性系统分析（第四版，吴大正主编）——信号与系统

 

 

目录

1.1  绪言

1.2  信号

1.连续信号与离散信号

2.周期信号和非周期信号

3.实信号和复信号

4.能量信号和功率信号

1.3  信号的基本运算

1.加法和乘法

2.反转和平移

3.尺度变换（横坐标展缩）

1.4  阶跃函数和冲激函数

1.阶跃函数和冲激函数

2.冲激函数的广义函数定义

3.冲激函数的导数和积分

4.冲击函数的性质

1.5  系统的描述

1. 系统的数学模型

2.系统的框图表示

1.6  系统的特性和分析方法

1.线性

2.时不变性

3.因果性

4.稳定性

5.LTI系统分析方法概述

 

1.1  绪言

（前前一段时间准备蓝桥杯，前一段时间在准备十佳标兵，所以对于学习上的事情感觉不够多，现在要腾出很多时间来开始写写信号，写写数理方程，蓝桥的很多代码也忘了，所以有空也会写写蓝桥，要是后续课程有需要，也写一写后边的课程，一定要坚持下来，加油！）

信号与系统首先要知道什么是信号什么是系统？？？

信号：随时间，空间变化的物理量或者物理现象。

系统：指的是若干相互关联，互相作用的事实按一定规律组合而成的具有特定功能的整体。

信号与系统的关系：

信号与线性系统分析（第四版，吴大正主编）——信号与系统_第1张图片

 

 信号的决定因素——信息

所以：信号是信息的载体，信息决定信号。

信号主要是：电、光、声、磁、机械、热等

信息主要是：语言、文字、图像等

信号和信息的关系：

信号与线性系统分析（第四版，吴大正主编）——信号与系统_第2张图片

 

 

 

1.2  信号

确定信号：如果一个信号可以用一个确定的时间函数（或序列）表示，就称其为确定信号（或规则信号）。

随机信号：幅度未可预知但又服从一定统计特性的信号，又称不确定信号。

（因为确定信号是基础，所以接下来讨论的都是确定信号）。

1.连续信号与离散信号

区分：根据定义域的特点可将信号分为连续信号和离散信号。

连续信号：在连续时间范围内（-∞

如：阶跃函数（取1的时候不包括0）

 

离散信号：“离散”是指信号的定义域——时间（或其他量）是离散的，它之取某些规定的值。（可闭合表示，也可以列举表示）

如单位阶跃序列：

单位阶跃序列定义为

ε（k）=0，k<0

ε（k）=1，k=0

ε（k）=1，k>0

它类似于连续时间信号中的单位阶跃信号ε（t）

（但应注意ε（t）在t=0处发生跃变，所以在t=0此点常常不予定义或定义为t=0.5），

而单位阶跃序列在ε（k）在t=0处为1。

 

2.周期信号和非周期信号

周期函数：定义在（-∞，+∞）区间，每隔一定的时间T（或整数N），按相同规律重复变化的信号。

连续周期信号可表示为

                        f(t) = f(t + mT),  m = 0, \pm1,\pm2，…… （周期T为最小正周期）

离散周期信号可表示为

                      f(t) = f(k + mN), m = 0, \pm1,\pm2，……

对于一个三角函数（\sin（\betak + \theta））

                     当    \frac{2\pi }{\beta }   =  N（正整数）， N为其周期；

                    当   \frac{2\pi }{\beta }  =  M / N (有理数)， M为其周期；

                    当 \frac{2\pi }{\beta }  =  无理数，则该函数为非周期；

3.实信号和复信号

实信号：物理可实现的信号常常是时间t（或k）的实函数（或序列），其在各时刻的函数（或序列）值为实数，如单边指数信号，正弦信号（正弦，余弦统称为正弦信号）等，称为实函数。

复信号：函数（或序列）值为复数的信号成为复信号，做常用的是复指数信号。（一个复指数信号可以分解为实、虚两部分）

例如：

其中

  

借助欧拉公式展开，可得                                

              （欧拉公式为： formula）

此结果表明，一个复指数信号可分为实、虚两部分。其中，实部包含余弦信号，虚部则为正弦信号。

4.能量信号和功率信号

连续信号f(t)

信号能量定义为在区间（-∞，+∞）中信号f(t)的能量，用字母E表示，即

                           {\color{Red} }{\color{Red} E\equiv \lim_{a \to\infty} \int_{-a}^{ a} |f(t)|^2dt}

信号功率定义为在区间（-∞，+∞）中信号f(t)的平均功率，用字母P表示，即

                         {\color{Red} P\equiv \lim_{a \to\infty }\frac{1}{2a}\int_{-a}^{a}|f(t)|^2dt}

若信号f(t)的能量有界（即0,这时P = 0），则称其为能量有限信号（持续时间有限），简称能量信号。

若信号f(t)的功率有界（即0,这时E = \infty），则称其为功率有限信号（如有始信号，周期信号，直流信号），简称功率信号。

离散信号f(k)

离散信号有时也需要讨论能量和功率，

序列f(k)的能量定义为

                                     {\color{Red} }{\color{Red} E\equiv \lim_{N \to\infty} \sum_{k=-N}^{N} |f(k)|^2}

序列f(k)的功率的定义为

                                   {\color{Red} }{\color{Red} E\equiv \lim_{N \to\infty}\frac{1}{2N+1} \sum_{k=-N}^{N} |f(k)|^2}f_{1}(\cdot )

 

1.3  信号的基本运算

1.加法和乘法

连续信号f(t)

信号f_{1}(\cdot )与f_{2}(\cdot )之和（瞬时和）是指同一瞬时两信号之值对应相加所构成的“和信号”，

                      即     {\color{Red} f(\cdot ) =f_{1}(\cdot )+f_{2}(\cdot )}          (例如调音台，将音乐与语音混合在一起)

信号f_{1}(\cdot )与f_{2}(\cdot )之积是指同一瞬时两信号之值对应相乘所构成的“积信号”，

                      即        {\color{Red} f(\cdot ) =f_{1}(\cdot )f_{2}(\cdot )}           （例如收音机的调幅信号，是将音频信号加载到被称为载波的正弦信号上）

离散信号f(k)

离散序列相加（相乘）可采用对应样点的值分别相加（或相乘）的方法来计算。

2.反转和平移

反转：将信号f(t)[或f(k)]中的自变量t（或k）转换为-t（或k）。——几何含义为将信号f(\cdot )以纵坐标为轴反转（或称反折）

平移:    

          连续信号f(t)

             对于连续信号f(t),若常数  t_{0} >0, 延时信号f(t-{t_{0}})  是将原信号沿t轴正方向平移 t_{0}时间       

                                                               延时信号f(t+{t_{0}})  是将原信号沿t轴负方向平移 t_{0}时间

        离散信号f(k)             

             对于离散信号f(t),若常数  k_{0} >0, 延时信号f(k-{k_{0}})  是将原信号沿k轴正方向平移 k_{0}时间       

                                                               延时信号f(k+{k_{0}})  是将原信号沿k轴负方向平移 k_{0}时间

平移和反转的先后顺序：要先平移后反转

3.尺度变换（横坐标展缩）

要想将信号横坐标的尺寸展宽或者压缩（常称为尺度变换），可将变量at(a为非零常数)代替原信号f(t)的自变量t，得到信号f(at)。

 连续信号f(t)

               f(t) ----->f(at)

          若|a| > 1,则以原点为基准压缩   \frac{1}{|a|},

         若|a| < 1,则以原点为基准展宽   \frac{1}{|a|},         （信号在时域内压缩，在频域会展宽）

离散信号f(k)   

           f(k) ----->f(ak) ,要求ak是整数，离散信号进行尺度变换常常会丢失原信号的部分信息，因而不能将f(ak)看作f(k)的压缩或者展宽。   

 

总结：已知f(t),求f(at+b) ：  要先平移，再反转，最后尺度变换（所有变得都是自变量）

          已知f(at+b),求f(t) ：  要先尺度变换，再反转，最后再平移。

1.4  阶跃函数和冲激函数

阶跃函数和冲激函数不同于普通的函数，称为奇异函数。

1.阶跃函数和冲激函数

阶跃函数

冲激函数

            

狄拉克（Dirac）给出了冲激函数的另一种定义

（1） ， 

（2） 

冲激函数与阶跃函数的关系

{\color{Red} \delta (t)=\frac{\mathrm{d}\varepsilon (t) }{\mathrm{d} t}}

{\color{Red} \varepsilon (t)= \int_{-\infty }^{t}\delta (x)dx}

2.冲激函数的广义函数定义

粗浅的说，广义函数是这样定义的，选择一类性能良好的函数\varphi (t),称为检验函数（它相当于定义域），一个广义函数g(t)是对检验函数空间中每个函数\varphi (t)赋予一个数值N的映射，该数与广义函数g(t)和检验函数有\varphi (t)有关，记作 N\left [ g(t),\varphi (t) \right ]

通常广义函数g(t)可写为

                              \int_{-\infty }^{\infty }g(t)\varphi (t)dt = N\left [ g(t),\varphi (t) \right ]

式中的检验函数\varphi (t)是连续的，具有任意阶导数，且本身及其各阶导数在无限远处急速下降的普通函数。（本身即无穷阶导数为零）

 

若

                     \int_{-\infty }^{\infty }f(t)\varphi (t)dt = N\left [ f(t),\varphi (t) \right ] = \int_{-\infty }^{\infty }g(t)\varphi (t)dt = N\left [ g(t),\varphi (t) \right ] 

就认为两个广义函数相等，并记作f(t) = g(t)

按广义函数理论，冲激函数\delta (t)由下式

                             {\color{Red} \int_{-\infty }^{\infty }\delta (t)\varphi (t)dt = \varphi (0)}

单位阶跃函数\varepsilon (t)的定义为

                             \int_{-\infty }^{\infty }\varepsilon (t)\varphi (t)dt=\int_{0}^{\infty }\varphi (t)dt

 

3.冲激函数的导数和积分

冲激函数\delta (t)的一阶导数\delta {}'(t)的定义为

                                       {\color{Red} \int_{-\infty }^{\infty }\delta {}'(t)\varphi (t)dt = -{\varphi }'(0)}

\delta ^n(t) = \frac{d^n\delta (t)}{dt^n}  :   {\color{Red} \int_{-\infty }^{\infty }\delta ^n(t)\varphi (t)dt = (-1)^n\varphi ^n(0)}

\delta (t)，\delta {}'(t)  的积分为：

                           \varepsilon (t) = \int_{-\infty }^{t }\delta (x)dx

                           \delta (t) = \int_{-\infty }^{t }\delta {}'(x)dx

4.冲击函数的性质

   一、以普通函数的乘积

          1.    {\color{Red}f(t)\delta (t)=f(0)\delta (t) }

          2.   {\color{Red}\int_{-\infty }^{\infty }f(t)\delta (t)dt=f(0)}

          3.  {\color{Red} f(t)\delta {}'(t)=f(0)\delta{}' (t)-f{}'(0)\delta (t)}

          4.   {\color{Red} {\int_{-\infty }^{\infty }}f(t)\delta {}'(t)=-f{}'(0)}

二、位移

          1.{\color{Red} \int_{-\infty }^{\infty }\delta (t-t_{1})\varphi (t)dt = \varphi (t_{1})}

          2.{\color{Red} \int_{-\infty }^{\infty }\delta {}'(t-t_{1})\varphi (t)dt=-\varphi {}'(t_{1})} 

          3.{\color{Red}f(t)\delta (t-t_{1})=f(t_{1})\delta (t-t_{1}) }

          4.{\color{Red} \int_{-\infty }^{\infty }\delta (t-t_{1})f (t)dt = f (t_{1})}

          5.{\color{Red} f(t)\delta {}'(t-t_{1})=f(t_{1})\delta {}'(t-t_{1})-f{}'(t_{1})\delta (t-t_{1})}

          6.{\color{Red} \int_{-\infty }^{\infty }f(t)\delta {}'(t-t_{1})dt=-f{}'(t_{1})}

  间断点：当信号有第一类间断点时，其一阶导数将在间断点处出现冲激，间断点处向上突跳时出现正冲激，向下突跳时出现负冲激，其强度等于突跳的幅度。

三、尺度变换

          

1.5  系统的描述

1. 系统的数学模型

2.系统的框图表示

1.6  系统的特性和分析方法

1.线性

2.时不变性

3.因果性

4.稳定性

5.LTI系统分析方法概述

 

 

你可能感兴趣的:(信号与系统)

按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他