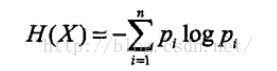机器学习之决策树
决策树是一种基本的分类与回归方法。这里主要讨论用于分类的决策树。
优点:具有可读性,分类速度快;
决策树学习通常包括三个步骤:特征选择、决策树的生成和决策树的修剪;
决策树学习 的思想来源主要是ID3算法、C4.5算法以及CART算法;
1 理论学习
决策树模型:
分类决策树模型是一种描述对实例进行分类的树形结构。决策树有节点(node)和有向边(directed edge)组成。节点有两种类型:内部节点和叶节点。内部节点标识一个特征或属性,叶节点标识一个类;
用决策树分类,从根节点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子节点;这时,每一个子节点对应该特征一个取值,如此递归低对实例进行测试并分配,直至达到叶子节点。最后实例被分到叶节点的类中。
决策树的if-then规则
可以将决策树看成一个if-then规则的集合;规则如下:将决策树的根节点到叶节点的每一条路径建立一条规则;路径上内部节点的特征对应着规则的条件,而叶节点的类对应着规则的结论。if-then规则集合有一个重要的性质:互斥并且完备;这就是每一个实例都被一条路径或者一条规则所覆盖,而且只被一条路径或者一条规则所覆盖。
决策树与条件概率分布:
决策树还表示给定特征条件下类的条件概率分布。这一条件概率分布定义在特征空间的一个划分上。将特征空间划分为互不相交的单元区域,并在每个单元定义一个类的概率分布就构成了一个条件概率分布。决策树的一条路径对应于划分中的一个单元。决策树所表示的条件概率有各个单元给定条件下的类的条件概率分布组成。假设X为标识特征的随机变量,Y为表示类的随机变量,那么这个条件概率分布可以表示为P(Y|X)。X取值给定划分下单元的集合,Y取值类的集合。
下图表示了特种空间的一个划分。大正方形表示特征空间。这个大正方形被若干个小矩形分割,每个小矩形表示一个单元。特征空间划分上的单元构成了一个集合,X取值为单元的集合。假设只有两类正类负类,Y=+1 -1;小矩形数字表示单元的类。第二个图表示给定条件下类的条件概率分布。P(Y=+1|X=c)>0.5时属于正类,实际上对应的就是矩形框的面积。
决策树的学习:
决策树的学习,假设给定训练数据集
其中 为输入实例(特征向量),n为特征个数,
为输入实例(特征向量),n为特征个数,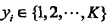 为类的标记,
为类的标记, ,
,![]() N为样本容量.。学习的目标是根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。
N为样本容量.。学习的目标是根据给定的训练数据集构建一个决策树模型,使它能够对实例进行正确的分类。
决策树学习本质上试从训练数据集中归纳出一组分类规则。与训练数据集不相矛盾的决策树可能有多个,也可能一个也没有。我们需要的是一个与训练数据矛盾较小的决策树,同时具有很好的泛化能力。从另一个角度看,决策树学习是有训练数据集估计条件概率模型。基于特征空间划分的类的条件概率模型有无数个,我们选择的条件概率模型应该不仅对训练数据有很好的拟合,而且对未知数据也有很好的预测。
决策树学习的损失函数通常是正则化的极大似然函数。决策树学习的策略是一损失函数为目标函数的最小化。
决策树学习算法通常是一个递归低选择最优特征,并根据特征对数据进行分割,使得对应各个子数据集有一个最好的分类过程。首先构建根节点,将训练数据放到根节点,选择一个最优特征,按照这个特征将训练集分为各个子集,使各个子集有一个当前条件下最好的分类。如果已经能够被基本正确分类,那么构建叶子节点,并将这些子集分到所对应的叶节点中去;如果还有子集不能被正确分类,那么对子集继续选择最优特征,直到没有合适的特征为止。
决策树表示一个概率分布,深浅不同的决策树对应着不同复杂度的概率模型。决策树的生成对应于模型的局部选择,决策树的剪枝对应于模型的全局选择。决策树的生成只考虑局部最优,相对地,决策树的剪枝则考虑全局最优。
特征选择:
特征选择在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率。
如果利用一个特征进行分类的结果与随机分类的结果没有很大差别,则呈这个特征是没有分类能力的。经验上扔掉这样的特征对决策树学习的精度影响不大。通常特征选择的准则是信息增益或信息增益比。
例子:
希望通过所给的训练数据学习一个贷款申请的决策树,用以对未来的贷款申请进行分类,即当新的客户提出贷款申请时,根据申请人的特征利用决策树决定是否批准贷款申请。
下图是从上表学习到的两个可能的决策树,分别由两个不同特征的根节点构成。a表示根节点的特征是年龄,有3个取值,对应于不同的取值有不同的子节点。b表示的根节点的特征是有工作,有两个取值,对应于不同的取值有不同的节点。两个决策树都可以从此延续下去。问题是,究竟选择哪个特征更好些,这就要求确定选择特征的准则。直观上,如果一个特征具有更好的分类能力,或者说,按照这一特征将训练数据集分割成子集,是的各个子集在当前条件下有最好的分类,那么久应该选择这个特征。信息增益就能很好地表示这一直观的准则。
信息增益:
为了方便说明,先给出熵和条件熵的定义。
在信息论与概率统计中,熵是表示随机变量不确定性的度量。设X是一个取有限个值的离散随机变量,其概率分布为P(X=xi)=pi
则随机变量X的熵的定义为
熵只依赖于X的分布,而与X的取值无关,所以X的熵记做H(p)
熵越大,随机变量的不确定性就越大,从定义可以验证
0<=H(P)<=logn
熵H(P)随着概率p变化的曲线如下图:
设随机变量(X,Y),其联合概率分布为
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X),定义为X给定条件下Y的条件概率分布的熵对X的数学期望
信息增益表示得知特征X的信息而使的类Y的信息不确定性减少的程度。
信息增益:
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即
g(D,A)=H(D)-H(D|A)
H(D)表示数据集D的不确定性,H(D|A)表示在特征A条件下对数据集D进行分类的不确定性。那么他们的差,即信息增益,表示由于特征A而使得对数据集D的分类的不确定性减少的程度。显然,对于数据集D而言,信息增益依赖于特征,不同的特征往往具有不同的信息增益。信息增益大的特征具有更强的分类能力。
信息增益比:
决策树生成:
ID3算法
核心就是在决策树各个节点上应用信息增益准则选择特征,递归低构建决策树。具体方法:从根节点开始,对节点计算所有可能的特征信息增益,选择信息增益最大的特征作为节点的特征,由该特征的不同取值作为子节点;在对子节点递归调用以上方法,构建决策树;知道所有特征信息增益均很小或没有特征可以选择为止,最后得到一个决策树。
C4.5算法,和ID3类似,不同是使用信息增益比来选择最优特征
决策树的剪枝:
为了防止过拟合,同时考虑模型复杂度