2019.2.27热身赛

好久没打ACM了，这次热身赛中也基本是水题，只AC了ABCD

A.New Year Transportation
题目大意：
给出n，k以及n-1个数a[i]，a[i]是前进的个数，从1出发，问能否通过a[i]到达k？
水题，模拟

B.Contest
题目大意：
给出a,b,c,d，通过公式计算得分判断结果。
a和c是Misha对应的p和t
b和d是Vasya对应的p和t
问Misha和Vasya谁赢了？
水题，计算比较point1和point2即可

C.Watching a movie
题目大意：
给出n,x,n行l[i]和r[i]
遥控器有2种按钮：1.不快进 2.快进x分钟
电影中有n个精彩片段，时间段是l[i]和r[i]，要求看完所有的精彩片段，最少需要花费多少分钟？时间从第1分钟开始。
题解：
因为输入中下一个片段的起点大于前一个片段的终点(l[i+1]>r[i]）所以可以不用排序直接顺序求解
设pos为当前分钟 ans为答案
只要当前分钟快进x后还是小于等于l[i]，那么就选择快进 (pos+x<=l[i])
不满足条件时
ans+=r[i]-pos+1; //看完片段消耗的时间
pos=r[i]+1; //看完片段后的时间
代码：

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 3e4+7;
const int mod = 10007;
typedef long long LL;
int n,x;
int l[100],r[100];
int pos=1,ans;
int main()
{
    scanf("%d %d",&n,&x);
    for(int i=0;i<n;i++)
        scanf("%d %d",&l[i],&r[i]);
    for(int i=0;i<n;i++)
    {
        while(pos+x<=l[i])
        {
            pos+=x;
        }   
        ans+=r[i]-pos+1;
        pos=r[i]+1;
    }
    printf("%d\n",ans);
    return 0;
}

D.Crazy Town
题目大意：
给2个点A(x1,y1) B(x2,y2) 再给出n条直线的参数a,b,c ax+by+c=0
n条直线把平面划分成了若干块，每一步可以跨越1块，问A所在的块到B所在的块最少需要走几步？
题解：
原本看到这题就想把AB连起来得到直线L,然后分别与n条直线联立求解得到n个点，判断点是否在AB的矩形范围内，在的话就ans++
但是WA在了text3，偷偷上cf看了一下样例，是个大数据。。。貌似double的精度不太够（long double也不行）
后来突然意识到可以不用解方程，只要A,B两点在某条直线的两侧，那么直线L与该条直线的交点就落在AB矩形内，那么就把A,B两点坐标代入直线方程，异号的话就ans++
再此顺便写一下两条直线方程的解：

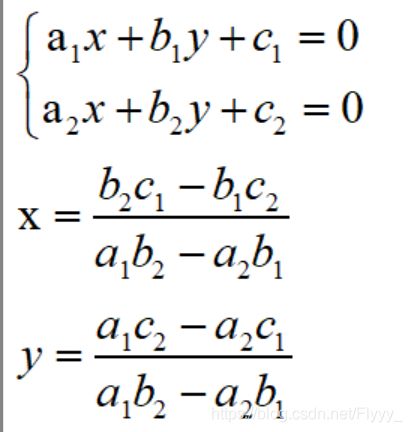
代码：

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 1e5+7;
const int mod = 10007;
typedef long long LL;
double x1,y1,x2,y2;
int n;
double a[305],b[305],c[305];
int ans=0;
int main()
{
    scanf("%lf %lf %lf %lf",&x1,&y1,&x2,&y2);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%lf %lf %lf",&a[i],&b[i],&c[i]);
    for(int i=1;i<=n;i++)
    {
        double temp1=a[i]*x1+b[i]*y1+c[i];
        double temp2=a[i]*x2+b[i]*y2+c[i];
        if(temp1*temp2<0)
            ans++;
    }
    printf("%d\n",ans);
    return 0;
}

E.New Year Permutation
题目大意：
给一个长度为n的数组p[]，大小为n*n的01矩阵A。
若存在另一个数组a[]，且存在1个整数k满足
a[0]==p[0],a[1]==p[1]…a[k-1]==p[k-1],a[k] 则称a[]比p[]漂亮
现在p[]里面的某些数字可以交换
矩阵A[i][j]=1表示p[i]和p[j]可交换
输出漂亮程度最高的数组a[]
题解：
把A看成邻接矩阵，A[i][j]=1表示p[i]和p[j]之间有一条边
可以看出最终答案数字小的要越往前越好
假设要求第i个位置的答案，从p[i] dfs遍历，找出相连的边的最小的数字，并继续递归检查同一连通块内的结点，这样就能确保第i个位置的答案一定是当前最小的数字，用ok[]记录已经找到的答案
代码：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 3e5+7;
const int inf = 1e9+7;
typedef long long LL;
int n;
int p[307];
char A[307][307];
int vis[307],ok[307];
int ans;

void dfs(int pos)
{
    if(!ok[p[pos]])
        ans=min(ans,p[pos]);
    vis[pos]=1;
    for(int i=0;i<n;i++)
        if(A[pos][i]=='1' && !vis[i])
            dfs(i);
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%d",&p[i]);
    for(int i=0;i<n;i++)
        scanf("%s",A[i]);

    for(int i=0;i<n;i++)
    {
        memset(vis,0,sizeof(vis));
        ans=n;
        dfs(i);
        ok[ans]=1;
        printf("%d ",ans);
    }
    printf("\n");
	return 0;
}

F.New Year Book Reading
题目大意：
有n本书堆在一起，每本书的重量为w[i]，Jaehyun要看m本书，看的顺序为b[i]
书只堆了一堆，要看某本书时，要把这本书上面的书抬起来，取走这本书，放下之前抬起的书，看完后再把这本书放在最顶部。问看完m本书需要耗费的最少力气是多少？（消耗的力气=抬起的书的重量和）
题解：
只要知道了这堆书一开始的堆叠状态，那么就可以计算出消耗的力气。所以问题在于确定书的初始状态。。。。做的时候实在毫无头绪，不知道怎么确定，写了几个样例就猜初始状态跟b[i]有关，是根据b[i]的数字的出现顺序来确定的（证明方法之后找找）
例如b[i]= 1 2 1 2 3
那么书的初始状态就是1 2 3 (左边是顶)
b[i]= 1 2 4 2 1 4 3 3 4
那么书的初始状态就是1 2 4 3 (左边是顶)
stack数组存放书的堆叠状态
每次遍历stack数组，编号跟b[i]不同就把编号暂时存放在temp里
若出现相同编号了，把stack[0]赋值为b[i]，temp接着复制到stack中并计算ans
代码：

#include 
#include 
#include 
#include 
#include 
using namespace std;
const int maxn = 1e5+7;
const int mod = 10007;
typedef long long LL;
int n,m;
int w[507],b[1007];
int vis[507],stack[507],temp[507],len;
LL ans;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&w[i]);
    for(int i=1;i<=m;i++)
        scanf("%d",&b[i]);
    for(int i=1;i<=m && len<n;i++)
    {
        if(!vis[b[i]])
        {
            vis[b[i]]=1;
            stack[len++]=b[i];
        }
    }
    for(int i=1;i<=m;i++)
    {
        int id=b[i];
        len=0;
        for(int j=0;j<n;j++)
        {
            if(stack[j]==id)
            {
                break;
            }
            else
            {
                temp[++len]=stack[j];
            }
        }
        stack[0]=id;
        for(int j=1;j<=len;j++)
        {
            stack[j]=temp[j];
            ans+=w[temp[j]];
        }
    }
    printf("%lld\n",ans);
    return 0;
}