COCI 2016/2017 Round #2 题解
COCI 2016/2017 Round #2
Go
题目翻译
分析
注意题目是先提供糖果再返还,所以我们不能直接硬除。
按题意暴力模拟即可,复杂度最高只有约 4 × 1 0 5 4\times 10^5 4×105,可以过。
参考代码
#includeTavan
题目翻译
分析
首先想到的应该是暴力回溯法。(做法不解释,自己看注释)
我们画一下解答树可以发现一些规律(以样例一为例,如下图所示):
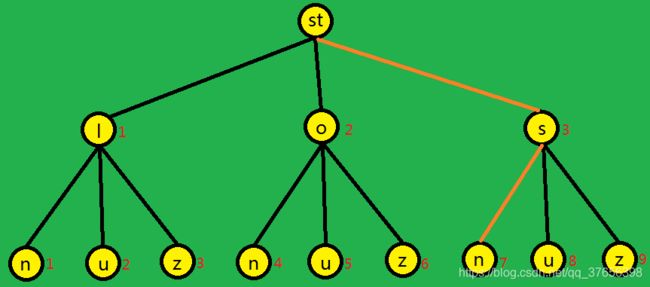
我们在每层节点放一个编号(红字),答案路径为橙色。
不难发现最下一层编号为 X X X的节点就是答案,只要沿着路径往回就可以了。
这个操作可以简单利用除法和取余来完成,具体详见代码。
参考代码
#include ans;
int cnt;
void DFS(int num) {
if(num>M) {
cnt++;
if(cnt==X) {
for(int i=0,j=0;i
char ans[Maxn+5];
int main() {
freopen("tavan.in","r",stdin);
freopen("tavan.out","w",stdout);
scanf("%d %d %d %d\n",&N,&M,&K,&X);
scanf("%s\n",S);
for(int i=1;i<=M;i++) {
scanf("%s\n",s[i]);
sort(s[i],s[i]+K);
}
// DFS(1);
for(int i=M;i>=1;i--) {
int t=(X-1)%K;
ans[i]=s[i][t];
if(X%K==0)X/=K;
else X=X/K+1;
}
for(int i=0,j=1;i<N;i++) {
if(S[i]=='#') {
putchar(ans[j]);
j++;
} else putchar(S[i]);
}
return 0;
}
Nizin
题目翻译
分析
这题我们可以贪心地从两边往中间走,不符回文就直接加就行了。
参考代码
#includeProsjecni
题目翻译
分析
这题真的是脑洞大开。。。。
我们分两种情况讨论:
对于奇数的矩阵,只需将 1 , 2 , 3 , … , N 2 1,2,3,\ldots,N^2 1,2,3,…,N2挨个填进去就可以了。
对于偶数的矩阵:
当 N = 2 N=2 N=2时,手推一下就可以发现不存在这样的矩阵。
当 N N N等于其他数时,我们可以采用如下步骤构造一个矩阵:
- 构造第 1 1 1行为 1 , 2 , 3 , … , N − 2 , N − 1 , N ( N − 1 ) 2 1,2,3,\ldots,N-2,N-1,\frac{N(N-1)}{2} 1,2,3,…,N−2,N−1,2N(N−1);
- 从第 2 2 2行开始,至第 N − 1 N-1 N−1行结束,每行每个元素较上一行递增 N ( N − 1 ) 2 \frac{N(N-1)}{2} 2N(N−1);
- 设第 N − 1 N-1 N−1行第一个数据为 a 1 a_1 a1,则第 N N N行的数字较第 N − 1 N-1 N−1行增加 1 + ( N − 2 ) ( N − 1 ) N ( N + 1 ) 2 − a 1 1+\frac{(N-2)(N-1)N(N+1)}{2}-a_1 1+2(N−2)(N−1)N(N+1)−a1。
接下来说明这个方法的合理性:
从第 1 1 1行到第 N − 1 N-1 N−1行,各个数字显然是不相等的,且该行平均数都在于第 N − 1 N-1 N−1列上。
根据构造方法,每一列的平均数也在第 N − 1 N-1 N−1行上。
我们可以知道,第 N − 1 N-1 N−1行最后一个数字是 N ( N − 1 ) 2 2 \frac{N(N-1)^2}{2} 2N(N−1)2,第 N N N行第一个数字是 1 + ( N − 2 ) ( N − 1 ) N ( N + 1 ) 2 1+\frac{(N-2)(N-1)N(N+1)}{2} 1+2(N−2)(N−1)N(N+1),画一下它们的函数图像:(如下图)
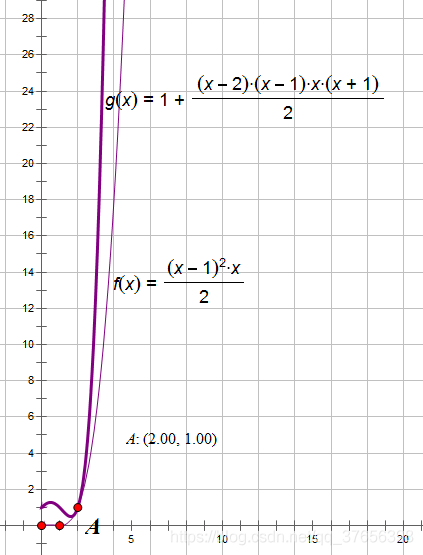
可以看出两函数有一个交点 A ( 2 , 1 ) A(2,1) A(2,1),且 g ( x ) g(x) g(x)增长速度明显要比 f ( x ) f(x) f(x)大,所以我们不必担心有重复的数字。
接下来说明最大的数字不会超过 1 0 9 10^9 109:
我们显然可以发现,第 N N N行第 N N N个数字是最大的,手推一下可以发现最后一个数的解析式为 ( N − 1 ) N ( N 2 − N − 1 ) 2 \frac{(N-1)N(N^2-N-1)}{2} 2(N−1)N(N2−N−1),把极限数据 100 100 100带进去得到结果 49000050 49000050 49000050没有超过 1 0 9 10^9 109。
参考代码
#include附送我考试时手写的一个简单的special judge (不能加到lemon中去):
#includeZamjene
题目翻译
分析
这题真的绕。。。。
我们先不管操作1,2。
考虑操作3,这一句话相当于将一堆有关联的东西连在一起并互相替换。这有点像并查集。所以我们就试一下吧。
如何证明排序?我们可以尝试 O ( N 2 ) O(N^2) O(N2)暴力查询,但显然是要超时的。。。
其实我们只需要记录能交换的位置上的数,与排好的对应位置上的数比较,只要有相同数量的数,我们就可以认为这个“云”是好的,即这几个位置可以排好序。
所以我们可以考虑哈希。。。如此对于两个云我们就可以 O ( 1 ) O(1) O(1)比较了。
所以,并查集只是一个载体。。。
对于操作1,我们应先将对应位置上的数从哈希表中删掉,并交换,最后不要忘掉再加回去。
对于操作2,我们在合并时把对应的哈希值加上即可。
对于操作3,我们只需利用查找两组对应哈希值相减是否都为0即可。
对应操作4,我们需要找到一个如下所示的云: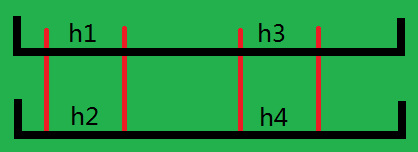
这四个云必须满足 h 1 + h 3 = h 2 + h 4 h_1+h_3=h_2+h_4 h1+h3=h2+h4,直接枚举不太好,我们移项一下:变为 h 1 − h 2 = − ( h 3 − h 4 ) h_1-h_2=-(h_3-h_4) h1−h2=−(h3−h4),这样我们就可以将对应的云的哈希值相减存在map里,最后数一遍就行了。
具体实现还是看代码吧。。。
参考代码
#include
#includeBurza
题目翻译
分析
对于深度大于 K K K的点,我们都可以舍掉,因为无论玩家怎么放,硬币最多向下 K K K次。
我们称深度为 K K K的结点为叶结点,并从左向右依次编号为 1 , 2 , … , N 1,2,\ldots ,N 1,2,…,N。。.。。(以下省略一万字)
(题解过于玄学,为避免阅读不适就省略,文后附官方题解截图,原比赛讨论链接)
简而言之,我们通过贪心的方法可以发现,当 K 2 ≥ N K^2\ge N K2≥N时,无论如何都是有解的。
当 K 2 < N K^2<N K2<N时,我们可以利用状压DP求出来,这部分可以参考lsk大佬的后半部分题解。
参考代码
#include






