深度搜索处理问题的关键 --- 做leetcode深度搜索类题目小结

 

 

1.深度优先搜索中的关键

2.深度优先搜索小结

3.深度优先搜索和回溯法的区别

4.深度优先搜索与递归的区别

---

1.深度优先搜索中的关键

深度搜索算法通常用来 解决 全排列，不重复组合，分组问题，多条路径，路径的条数等等

对于深度优先搜索，最重要的参数有两个，第一是 深度搜索的次数 step，可以看做需要将待搜索的结果放入到 step 个盒子中，直到放满为止。

第二个是每一次 深度搜索的开始位置start, 主要控制的是每次深度搜索的范围

比如：

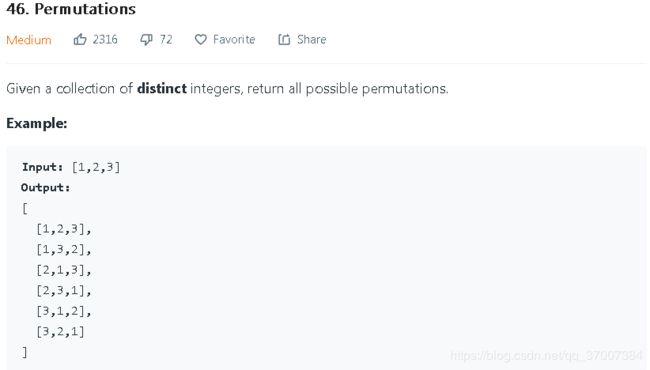
对于全排列问题，求[1,2,3]的全排列问题，此时我们可以将问题转化为 将 1,2,3按不同的次序放入到三个盒子中，我们需要的是控制深度搜索的次数step，这个次数就是我们深度搜索的结束条件（收敛条件）

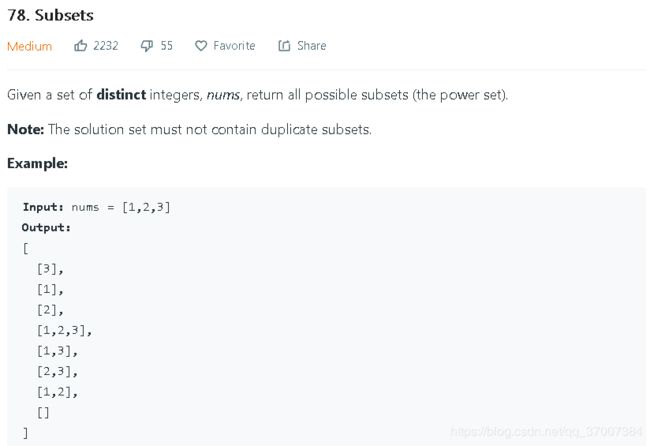
对于求子集问题，求[1,2,3]的全部子集（不能重复），与全排列不同，为了求出不重复的子集，我们需要使在1右边的元素永远在1的右边，也就是说，在第二次深度搜索时我们的搜索范围应该是[2,3]，此时我们并不控制深度搜索的次数，而是控制的是深度搜索开始的位置。

class Solution {
public:
    vector> permute(vector& nums) 
    {
        vector book(nums.size(),false);
        vector tmp;
        vector> res;
        dfs(nums,0,book,tmp,res);
        return res;
    }
    
private:
    void dfs(vector& nums,int step,vector&book,vector& tmp,vector>& res)
    {
        if(step == nums.size())
        {
            res.push_back(tmp);
            return;
        }
        for(int i = 0; i < nums.size();i++)
        {
            if(!book[i])
            {
                tmp.push_back(nums[i]);
                book[i] = true;
                dfs(nums,step+1,book,tmp,res);
                tmp.pop_back();
                book[i] = false;
            }
        }
    }
};

class Solution {
public:
    vector> subsets(vector& nums) 
    {
        vector> res;
        vector path;
        dfs(nums, 0, path, res);
        return res;
    }
private:
    void dfs(vector& nums, int start, vector& path, vector>& res)
    {
        res.push_back(path);
        
        for(int i = start; i < nums.size(); i++)//这里用的是start，控制每一次深搜的范围
        {
            path.push_back(nums[i]);
            dfs(nums,i+1,path,res);
            path.pop_back();
        }
    }
    
};

当然，有些情况下，我们即需要控制 深搜的次数 又需要控制每一次深搜的范围，这种问题典型特征是 分配出了要求的盒子数，

而且是组合问题

较简单的：

class Solution {
public:
    vector> combine(int n, int k) 
    {
        vector> res;
        vector path;
        dfs(n, k,1, 0, path, res);
        return res;
    }
    
private:
    void dfs(int n, int k,int start, int step, vector& path, vector>& res)
    {
        if(step == k)
        {
            res.push_back(path);
            return;
        }
        for(int i = start; i <= n; i++)
        {
            path.push_back(i);
            dfs(n,k,i+1,step+1,path,res);
            path.pop_back();
        }
    }
};

较难的：

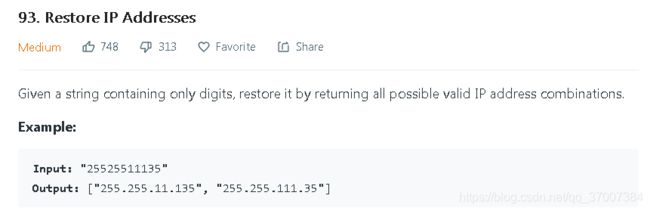
这一题目中，虽然没有明确说拆分为的盒子数，但是根据IP的特征，应该拆分为4个盒子

同时，这也是一个组合问题（只不过是字符串写在了一起而已），需要控制每次深度搜索的初始位置

class Solution {
public:
    vector restoreIpAddresses(string s) 
    {
        vector res;
        string path;
        if(s.size() > 12)
        {
            return res;
        }
        dfs(s, 0,0,path,res);
        return res;
    }
private:
    void dfs(string s, int start,int step,string path, vector& res)
    {
        if(start == s.size() && step == 4)
        {
            res.push_back(path);
            return;
        }
        for(int i = 1; i <= s.size();i++)
        {
            if(start + i > s.size())
            {
                return;
            }
            string section = s.substr(start,i);
            if(section.size() > 1 && section[0] == '0' || convert(section) > 255)
            {
                return;
            }

            //同时这里用了一个小技巧，因为是字符串，所以不能pop掉后面过来的字符串，所以选择下面这一种方式，来进行回溯
            dfs(s,start+i,step+1,step == 0 ? section : path + "." + section,res);
        }
    }
    int convert(string section)
    {
        int sum = 0;
        for(int i = 0; i < section.size(); i++)
        {
            sum = sum*10 + section[i] - '0';
        }
        return sum;
    }
    
};

对于二维空间的深度搜索，如果起点已经定下，则由此点开始向上下左右扩展即可，如果起点没有定下来，则在主调函数中进行遍历起点，并对每一个起点进行深度优先搜素，同时，如果深度搜索函数有返回值，则对其进行组合处理即可

起点确定下的二维深度搜索：

class Solution {
public:
    int uniquePaths(int m, int n) 
    {
        vector> book(m+1,vector(n+1,0));
        return dfs(m,n,0,0,book);   
    }
    
private:
    int dfs(int m, int n,int i,int j,vector>& book)
    {
        if( i == m-1 && j == n-1)//收敛条件
        {
            return 1;
        }
        if(i >= m || j >= n)
        {
            return 0;
        }
        return getbook(m,n,i+1,j,book) + getbook(m,n,i,j+1,book);        
    }
    
    int getbook(int m,int n,int i,int j,vector>& book)
    {
        if(book[i][j] > 0)
        {
            return book[i][j];
        }
        else
        {
            return book[i][j] = dfs(m,n,i,j,book);
        }
    }
    
};

起点不确定条件下的二维深度搜索：

class Solution {
public:
    bool exist(vector>& board, string word) 
    {
        int m = board.size();
        int n = board[0].size();
        vector> book(m,vector(n,false));
        
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n;j++)
            {
                if(exist(board,i,j,0,word,book))
                {
                    return true;
                }

            }
        }
        return false;
        
    }
private:
    bool exist(vector>& board,int i,int j,int step,string word,vector>& book)
    {
        if(step == word.size() )//注意：这个step必须为连续不断的step,不能断
        {
            return true;
        }
        if(i < 0 || j < 0 || i >= board.size() || j >= board[0].size())
        {
            return false;
        }
        if(book[i][j])
        {
            return false;
        }
        if(board[i][j] != word[step])
        {
            return false;
        }

        book[i][j] = true;
        bool res = exist(board,i+1,j,step+1,word,book) || exist(board,i,j+1,step+1,word,book) ||exist(board,i-1,j,step+1,word,book) || exist(board,i,j-1,step+1,word,book);
        book[i][j] = false;
        return res;
    }
};

2.深度优先搜索小结

深度优先搜索适用：

                         如果是递归数据结构，比如单链表，二叉树，集合，则一定可以用深度搜索，如果是非递归数据结构，如一维数组，二维数组，字符串，图等则概率小一些

                         明确深搜是求路径本身还是路径条数，前者则用一个数组 path来进行记录存储，后者不用存储路径

                        终止条件是什么？终止条件只的是不能扩展的末端节点，对于树，则是叶子节点

                        收敛条件是什么？收敛条件是指找到了一个合法解，很多时候终止条件和收敛条件是合二为一的，但两者代表的含义是不同的

                       剪枝加速，深度搜索的优点 是能在答案生成一半时就进行判断，舍弃不满足要求的答案，减少冗余搜索；利于题设中的各种信息，一旦判断此时的答案不会满足要求，则提前返回，避免冗余搜索

                     深度搜索代码模板：

void dfs(type *input,type* path,int step(int start),type *result)
{
    if(数据非法) return;
    if(step == input.size() (or start == input.size()))//收敛条件
    {
        将path放入 res中
        return;
    }
    if(可以剪枝) return;
    for(...) //执行所有可能的扩展操作
    {
        执行动作，修改path
        dfs(input,path,step+1(or start+1),res);
        恢复path;        
    }
}

3.深度优先搜索和回溯法的区别

回溯法＝ 深度搜索  ＋ 剪枝

深度搜索 准确的来讲，在搜索过程中会保留下来完整的树结构，即使遍历结果不满足答案，也会继续搜素下去，

而回溯法 是在深度搜索的过程中进行判断中间结果，如果中间结果不满足条件要求，则进行返回，不再搜索下去，

但是由于现在我们在深度搜索的过程中，或多或少会进行剪枝，所以这样来看两者并没有什么区别

 

4.深度优先搜索与递归的区别

深搜常常用递归来实现，二者常常同时出现，但是两者并不是同一个东西。

深搜，是一种算法，而递归是一种物理意义上的实现，递归和迭代是对应的。深搜可以用递归来实现，也可以用栈来实现，而递归，一般总用来实现深搜。

可以说，递归一定是深搜，深搜不一定用递归

递归有两种加速策略：一种是剪枝，对中间结果进行判断，提前返回（回溯），一种是加缓存，缓存中间结果，防止重复计算（动态规划），当然动态规划也可以用迭代来实现

还有一个问题：既然递归一定是深搜，那为什么要有两种术语呢？一般而言，在递归味道更浓的地方，一般用递归，比如在单链表，二叉树等递归数据结构上，而在图，数组等数据结构上，递归的比重不大，深搜的味道更浓，所以用深搜，但两者大部分情况下指同一回事。