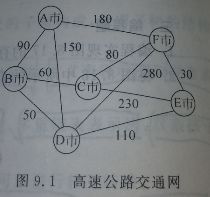


(一)用邻接矩阵解决图的编程问题 (此代码里面含有Dijkstra最短路径算法,在最后面)


using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 用邻接矩阵解决图的编程问题
{
class Program
{
static void Main(string[] args)
{
}
}
public class Node
{
private T data;//数据域
public T Data { get => data; set => data = value; }
public Node(T v)
{
data = v;
}
}
//图的基本操作
public interface IGraph
{
void SetNode(int index, Node v);//设置索引为index的顶点的信息
void SetEdge(Node v1, Node v2, int v);//在结点v1和v2之间添加权值为v的边
void SetEdge(Node v1, Node v2);//设置顶点v1,v2之间的边
void SetEdge(int index1, int index2);//设置索引为index1和index2的两个顶点之间的边
int GetEdge(Node v1, Node v2);//获取结点v1,v2之间的边
int GetEdge(int index1, int index2);//获取索引index1和index2的两个顶点之间的边
void DelEdge(Node v1, Node v2);//删除结点v1,v2之间的边
int GetNumOfVertex();//获取顶点的数目
int GetNumOfEdge();//获取边的数目
Node GetNode(int index);//根据索引获取图中的顶点
int GetIndex(Node v);//获取顶点v在顶点数组中的索引
bool IsEdge(Node v1, Node v2);//判断结点v1,v2之间是否存在边
bool IsNode(Node v);//判断v是否是图的顶点
}
public class GraphAdjMatrix : IGraph
{
private Node[] nodes;//顶点数组
private int[,] matrix;//邻接矩阵数组
private int numEdges;//边的数目
//初始化邻接矩阵
public GraphAdjMatrix(int n)
{
nodes = new Node[n];
matrix = new int[n, n];
}
///
/// 获取边的数目
///
///
public int GetNumOfEdge()
{
return numEdges;
}
///
/// 获取顶点的数目
///
///
public int GetNumOfVertex()
{
return nodes.Length;
}
///
/// 获取索引index1和index2的两个顶点之间的边
///
///
///
///
public int GetEdge(int index1, int index2)
{
return matrix[index1, index2];
}
///
/// 设置索引为index1和index2的两个顶点之间的边
///
///
///
public void SetEdge(int index1, int index2)
{
matrix[index1, index2] = 1;
}
///
/// 设置索引为index的顶点的信息
///
///
///
public void SetNode(int index, Node v)
{
nodes[index] = v;
}
///
/// 获取索引为index的顶点的信息
///
///
///
public Node GetNode(int index)
{
return nodes[index];
}
///
/// 判断结点v是否是图的顶点
///
///
///
public bool IsNode(Node v)
{
foreach (Node node in nodes)
{
if (v.Equals(node))
{
return true;
}
}
return false;
}
///
/// 获取顶点v在顶点数组中的索引
///
///
///
public int GetIndex(Node v)
{
for (int i = 0; i < nodes.Length; i++)
{
if (nodes[i].Equals(v))
{
return i;
}
}
return -1;
}
///
/// 判断结点v1,v2之间是否存在边
///
///
///
///
public bool IsEdge(Node v1, Node v2)
{
if (!IsNode(v1) || !IsNode(v2))//如果结点v1,v2不是图的顶点
{
Console.WriteLine("Node is not belong to Graph");
return false;
}
if (matrix[GetIndex(v1), GetIndex(v2)] == 1)
{
return true;
}
else
{
return false;
}
}
///
/// 在结点v1和v2之间添加权值为v的边
///
///
///
///
public void SetEdge(Node v1, Node v2, int v)
{
if (!IsNode(v1) || !IsNode(v2))//如果结点v1,v2不是图的顶点
{
Console.WriteLine("Node is not belong to Graph");
return;
}
matrix[GetIndex(v1), GetIndex(v2)] = v;
matrix[GetIndex(v2), GetIndex(v1)] = v;
numEdges++;
//为计算最短路径新加的代码,用来将没有边的两个顶点间的权值设为无穷大
for (int i = 0; i < GetNumOfVertex (); i++)
{
for (int j = i+1; j < GetNumOfVertex (); j++)//???
{
if(matrix[i, j] == 0)
{
matrix[i, j] = int.MaxValue;//用整数的最大值代表无穷大
matrix[j, i] = int.MaxValue;
}
}
}
}
///
/// 设置顶点v1,v2之间的边
///
///
///
public void SetEdge(Node v1, Node v2)
{
SetEdge(v1, v2, 1);
}
///
/// 获取结点v1,v2之间的边
///
///
///
///
public int GetEdge(Node v1, Node v2)
{
if (!IsNode(v1) || !IsNode(v2))
{
Console.WriteLine("Node is not belong to Graph");
return 0;
}
return matrix[GetIndex(v1), GetIndex(v2)];
}
///
/// 删除结点v1,v2之间的边
///
///
///
public void DelEdge(Node v1, Node v2)
{
if (!IsNode(v1) || !IsNode(v2))
{
Console.WriteLine("Node is not belong to Graph");
return;
}
if (matrix[GetIndex(v1), GetIndex(v2)] == 1)
{
matrix[GetIndex(v1), GetIndex(v2)] = 0;
matrix[GetIndex(v2), GetIndex(v1)] = 0;
numEdges--;
}
}
#region Dijkstra最短路径算法
///
/// Dijkstra最短路径算法
///
///
///
public void Dijkstra(ref int[] distance, Node n)
{
int v = 0;
bool[] final = new bool[nodes.Length];
for (int i = 0; i < nodes.Length; i++)
{
final[i] = false;
distance[i] = matrix[GetIndex(n), i];
}
distance[GetIndex(n)] = 0;//n为源点
final[GetIndex(n)] = true;
for (int i = 0; i < nodes.Length; i++)//处理从源点到其余顶点的最短路径
{
int min = int.MaxValue;
for (int j = 0; j < nodes.Length; j++)//比较从源点到其余顶点的路径长度
{
if (!final[j])//从源点到j顶点的最短路径还没有找到
{
if (distance[j] < min)//从源点到j顶点的路径长度最小
{
v = j;
min = distance[j];
}
}
}
final[v] = true;//源点到顶点k的路径长度最小
for (int w = 0; w < nodes.Length; w++)//更新当前最短路径及距离
{
if (final[w] == false)
{
if (matrix[v, w] != int.MaxValue && (min + matrix[v, w] < distance[w]))
{
distance[w] = min + matrix[v, w];
}
}
}
}
}
#endregion
}
}
(二)用邻接表解决图的编程问题(已将深度优先搜索算法和广度优先搜索算法写进去了,在代码的最后面)

using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 用邻接表解决图的编程问题
{
class Program
{
static void Main(string[] args)
{
}
}
public class Node
{
private T data;//数据域
public T Data { get => data; set => data = value; }
public Node(T v)
{
data = v;
}
}
//邻接表结点类
public class AdjListNode
{
private int adjvex;//邻接顶点序号。注意:不是表示该结点相邻的结点的序号,而是表示自己的序号!不要被误导了
private int info;//存储边或弧相关的信息,如权值
private AdjListNode nextadj;//下一个邻接表结点
public int Adjvex { get => adjvex; set => adjvex = value; }
public int Info { get => info; set => info = value; }
public AdjListNode Nextadj { get => nextadj; set => nextadj = value; }
public AdjListNode (int adjvex)
{
this.adjvex = adjvex;
nextadj = null;
}
public AdjListNode (int adjvex,int info)
{
this.adjvex = adjvex;
this.info = info;
nextadj = null;
}
}
//顶点结点类
public class VexNode
{
private Node data;//图的顶点
private AdjListNode firstadj;//邻接表的第1个结点
public Node Data { get => data; set => data = value; }
public AdjListNode Firstadj { get => firstadj; set => firstadj = value; }
//初始化顶点结构
public VexNode (Node node)
{
data = node;
firstadj = null;
}
public VexNode (Node node,AdjListNode alNode)
{
data = node;
firstadj = alNode;
}
}
//图的基本操作
public interface IGraph
{
void SetNode(int index, Node v);//设置索引为index的顶点的信息
void SetEdge(Node v1, Node v2, int v);//在结点v1和v2之间添加权值为v的边
void SetEdge(Node v1, Node v2);//设置顶点v1,v2之间的边
void SetEdge(int index1, int index2);//设置索引为index1和index2的两个顶点之间的边
int GetEdge(Node v1, Node v2);//获取结点v1,v2之间的边
int GetEdge(int index1, int index2);//获取索引index1和index2的两个顶点之间的边
void DelEdge(Node v1, Node v2);//删除结点v1,v2之间的边
int GetNumOfVertex();//获取顶点的数目
int GetNumOfEdge();//获取边的数目
Node GetNode(int index);//根据索引获取图中的顶点
int GetIndex(Node v);//获取顶点v在顶点数组中的索引
bool IsEdge(Node v1, Node v2);//判断结点v1,v2之间是否存在边
bool IsNode(Node v);//判断v是否是图的顶点
}
public class GraphAdjList : IGraph
{
private VexNode[] adjList;//邻接表数组
///
/// 初始化邻接表
///
///
public GraphAdjList(Node[] nodes)
{
adjList = new VexNode[nodes.Length];
for (int i = 0; i < nodes .Length ; i++)
{
adjList[i] = new VexNode(nodes[i]);
}
}
///
/// 获取顶点的数目
///
///
public int GetNumOfVertex()
{
return adjList.Length;
}
///
/// 设置索引为index的顶点的信息
///
///
///
public void SetNode(int index, Node v)
{
adjList[index] = new VexNode(v);
}
///
/// 获取索引为index的顶点的信息
///
///
///
public Node GetNode(int index)
{
return adjList[index].Data;
}
///
/// 判断结点v是否是图的顶点
///
///
///
public bool IsNode(Node v)
{
foreach (VexNode node in adjList )
{
if(v.Equals (node .Data))
{
return true;
}
}
return false;
}
///
/// 获取顶点v在邻接表数组中的索引
///
///
///
public int GetIndex(Node v)
{
for (int i = 0; i < adjList .Length ; i++)
{
if(adjList [i].Data.Data.Equals (v.Data ))
{
return i;
}
}
return -1;
}
///
/// 判断结点v1,v2之间是否存在边
///
///
///
///
public bool IsEdge(Node v1, Node v2)
{
if(!IsNode (v1)||!IsNode(v2))
{
Console.WriteLine("Node is not belong to Graph");
return false;
}
AdjListNode p = adjList[GetIndex(v1)].Firstadj;
while (p!=null)
{
if(p.Adjvex ==GetIndex(v2))//???
{
return true;
}
p = p.Nextadj;
}
return false;
}
///
/// 获取边的数目
///
///
public int GetNumOfEdge()
{
int i = 0;
foreach (VexNode node in adjList )
{
AdjListNode p = node.Firstadj;
while (p!=null)
{
i++;
p = p.Nextadj;
}
}
return i / 2;
}
///
/// 在结点v1和v2之间添加权值为v的边
///
///
///
///
public void SetEdge(Node v1, Node v2, int v)
{
if(!IsNode (v1 )||!IsNode (v2 )||IsEdge(v1, v2))
{
Console.WriteLine("Node is not belong to Graph");
return;
}
if (v == 0)
{
return;
}
AdjListNode p;
p = new AdjListNode(GetIndex(v2), v);
if (adjList [GetIndex (v1)].Firstadj ==null)
{
adjList[GetIndex(v1)].Firstadj = p;
}
else
{
p.Nextadj = adjList[GetIndex(v1)].Firstadj;
adjList[GetIndex(v1)].Firstadj = p;
}
p = new AdjListNode(GetIndex(v1), v);
if (adjList[GetIndex(v2)].Firstadj == null)
{
adjList[GetIndex(v2)].Firstadj = p;
}
else
{
p.Nextadj = adjList[GetIndex(v2)].Firstadj;
adjList[GetIndex(v2)].Firstadj = p;
}
}
///
/// 设置顶点v1,v2之间的边
///
///
///
public void SetEdge(Node v1, Node v2)
{
SetEdge(v1, v2, 1);
}
///
/// 设置索引为index1和index2的两个顶点之间的边
///
///
///
public void SetEdge(int index1, int index2)
{
SetEdge(GetNode(index1), GetNode(index2), 1);
}
///
/// 获取索引index1和index2的两个顶点之间的边
///
///
///
///
public int GetEdge(int index1, int index2)
{
if(!IsNode (GetNode (index1 ))||!IsNode (GetNode (index2)))
{
Console.WriteLine("Node is not belong to Graph");
return 0;
}
AdjListNode p = adjList[index1].Firstadj;
while (p!=null)
{
if(p.Adjvex ==index2)
{
return p.Info;
}
p = p.Nextadj;
}
return 0;
}
///
/// 获取结点v1,v2之间的边
///
///
///
///
public int GetEdge(Node v1, Node v2)
{
AdjListNode p = adjList[GetIndex(v1)].Firstadj;
while (p!=null)
{
if(p.Adjvex ==GetIndex (v2))
{
return p.Info;
}
p = p.Nextadj;
}
return 0;
}
///
/// 删除结点v1,v2之间的边
///
///
///
public void DelEdge(Node v1, Node v2)//???
{
if (!IsNode(v1) || !IsNode(v2))
{
Console.WriteLine("Node is not belong to Graph");
return ;
}
if(IsEdge(v1, v2))
{
AdjListNode p = adjList[GetIndex(v1)].Firstadj;
AdjListNode pre = null;
while (p!=null)
{
if(p.Adjvex !=GetIndex (v2))
{
pre = p;
p = p.Nextadj;
}
}
pre.Nextadj = p.Nextadj;
p = adjList[GetIndex(v2)].Firstadj;
pre = null;
while (p!=null)
{
if(p.Adjvex !=GetIndex(v1))
{
pre = p;
p = p.Nextadj;
}
}
pre.Nextadj = p.Nextadj;
}
}
#region 图的遍历:深度优先搜索算法,广度优先搜索算法
private bool[] visited;
///
/// 深度优先搜索算法
///
///
///
public Node[] DFSAL(Node v)
{
int i = GetIndex(v);
int m = 0;
Node[] nodes = new Node[GetNumOfVertex()];
visited[i] = true;
Stack stack = new Stack();//需要导入命名空间:System.Collections
stack.Push(i);
while (stack.Count > 0)
{
int k = (int)stack.Pop();
nodes[m++] = adjList[k].Data;
AdjListNode p = adjList[k].Firstadj;
while (p != null)
{
if (visited[p.Adjvex] == false)
{
visited[p.Adjvex] = true;
stack.Push(p.Adjvex);
}
p = p.Nextadj;
}
}
for (int j = 0; j < visited.Length; j++)
{
if (visited[j] == false)
{
DFSAL(GetNode(j));
}
}
return nodes;
}
///
/// 广度优先搜索算法
///
///
///
public Node[] BFSAL(Node v)
{
int i = GetIndex(v);
int m = 0;
Node[] nodes = new Node[GetNumOfVertex()];
visited[i] = true;
Queue queue = new Queue();//需要导入命名空间:System.Collections
queue.Enqueue(i);
while (queue.Count > 0)
{
int k = (int)queue.Dequeue();
nodes[m++] = adjList[k].Data;
AdjListNode p = adjList[k].Firstadj;
while (p != null)
{
if (visited[p.Adjvex] == false)
{
visited[p.Adjvex] = true;
queue.Enqueue(p.Adjvex);
}
p = p.Nextadj;
}
}
for (int j = 0; j < visited.Length; j++)
{
if (visited[j] == false)
{
BFSAL(GetNode(j));
}
}
return nodes;
}
#endregion
}
}
(三)解决图的遍历问题(深度优先搜索,广度优先搜索)
1.深度优先搜索(代码在上面)

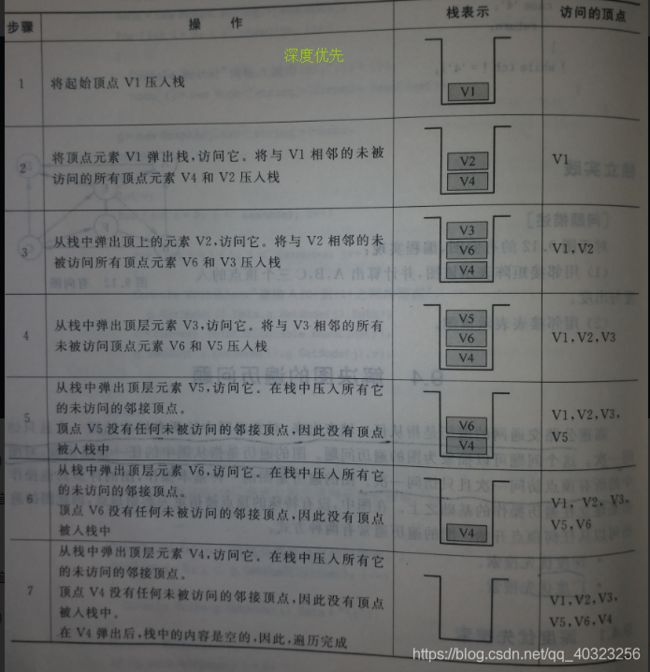
2.广度优先搜索(代码在上面)









