数据结构---哈希表

大部分来源小甲鱼数据结构视频

散列（哈希）技术是在记录的存储位置和它的关键字之间建立一个确定的关系（哈希函数），使得每个关键字key对应一个存储位置，
记录的存储位置=f(key)。
哈希函数是一种映射，设定灵活。
不同关键字可能会得到同一哈希地址即冲突。

哈希表概念：
根据设定的哈希函数H(key)和处理冲突的方法将一组关键字映像到一个有限的连续的存储空间（地址集）上，并以关键字在地址集中的“像”作为记录在表中的存储位置。

哈希表的查找步骤：
当存储记录时，通过散列函数计算出记录的散列地址
当查找记录时，我们通过同样的是散列函数计算记录的散列地址，并按此散列地址访问该记录
散列技术既是存储方法也是查找方法，且不需要迭代。

哈希函数的构造方法：
构造散列函数的两个基本原则
1 计算简单
2 分布均匀
***1.直接定址法
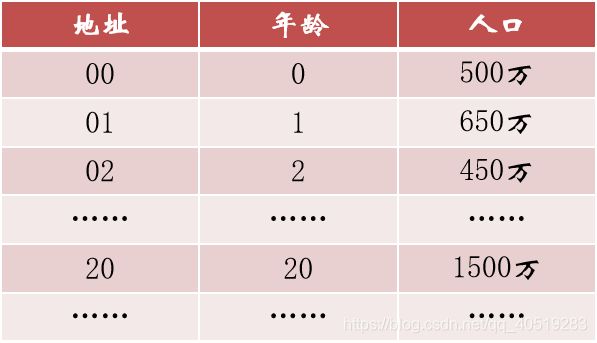
例一：有一个从1到100岁的人口数字统计表，其中，年龄作为关键字，哈希函数取关键字自身。
即：f(key) = key

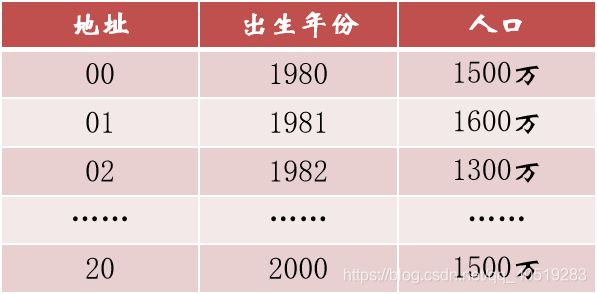
例二：如果现在要统计的是1980年以后出生的人口数，那么我们对出生年份这个关键字可以变换为：用年份减去1980的值来作为地址。
即：f(key) = key – 1980
f(key)=akey+b

实际中使用不多
2 数字分析法

数字分析法通常适合处理关键字位数比较大的情况，例如我们现在要存储某家公司员工登记表，如果用手机号作为关键字，那么我们发现抽取后面的四位数字作为散列地址是不错的选择。
3 平方取中法
平方取中法是将关键字平方之后取中间若干位数字作为散列地址。
适合不知关键字分布且位数少
4 折叠法
折叠法是将关键字从左到右分割成位数相等的几部分，然后将这几部分叠加求和，并按散列表表长取后几位作为散列地址
适合不知关键字分布且位数较多
5 除留余数法
此方法为最常用的构造散列函数方法，对于散列表长为m的散列函数计算公式为：
f(key) = key mod p(p<=m)

事实上，这个方法不仅可以对关键字直接取模，也可以通过折叠、平方取中后再取模。
例如下表，我们对有12个记录的关键字构造散列表时，就可以用f(key) = key mod 12的方法。

p的选择是关键，如果对于这个表格的关键字，p还选择12的话，那得到的情况未免也太糟糕了：

p的选择很重要，如果我们把p改为11，那结果就另当别论啦：

由众人经验得知：一般情况下，可以选p为质数或不包含小于20的质因数的合数
6 随机法
选择一个随机数，取关键字的随机函数值为它的散列地址。
即：f(key) = random(key)。
这里的random是随机函数，当关键字的长度不等时，采用这个方法构造散列函数是比较合适的

不同情况用不同哈希函数，考虑因素有：
计算散列地址所需的时间
关键字的长度
散列表的大小
关键字的分布情况
记录查找的频率

处理冲突的方法：
1 开放定址法
所谓的开放定址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。
它的公式是：
fi(key) = (f(key)+di) MOD m (di=1,2,…,m-1)
例：假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},使用除留余数法(m=12)求散列表

插入37时与25冲突则(37+1)MOD 12=2，则填入2中
di为增量序列，可有三种取法：
1 线性探测再散列
di=1,2,…,m-1
此种易堆积
2 二次探测再散列
di=1²,-1²,2²,-2²…,q²,-q²,q<=m/1
此中不易堆积
3 随机探测再散列
di是由一个随机函数获得的数列

2 再哈希法
fi(key) = RHi(key) (i=1,2,3,…k)
即换函数

3 链地址法
例：假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},同样使用除留余数法求散列表。

就像上例中所示有冲突直接在其后再插入一个形成链表。
4 公共溢出区法
例：假设关键字集合为{12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34},同样使用除留余数法求散列表。

建立两个表，一个基本表，一个溢出表，先将数据放入基本表若有冲突则按顺序放入溢出表，在查找时先查找基本表再查找溢出表，若都无则查找失败。

代码

#include 
#include 
#define HASHSIZE 12 //表长
#define NULLKEY -32768  //不会出现的值

typedef struct
{
    int *elem;//数据元素的基址，动态分配数组
    int count;//当前数据元素的个数
}HashTable;
//初始化哈希表
int InitHashTable(HashTable *H)
{
    H->count=HASHSIZE;
    H->elem=(int *)malloc(HASHSIZE*sizeof(int));
    if(!H->elem)//H->elem=NULL
    {
        return -1;
    }
    for(int i=0;ielem[i]=NULLKEY;
    }
    return 0;
}
 //除留余数法构造散列函数
 int Hash(int key)
 {
     return key%HASHSIZE;
 }
 //插入关键字到散列表
void insertHash(HashTable *H,int key)
{
    int addr;//地址
    addr=Hash(key);
    while(H->elem[addr]!=NULLKEY)//里面有数据则不等于，产生冲突，如果不为空,则冲突出现
    {
        //开放定址法 线性探测
        addr=(addr+1)%HASHSIZE;//找空位，找到空位把其放进去
    }
    H->elem[addr]=key;
}
//在散列表查找关键字
int searchHash(HashTable *H,int key)
{
    int addr=Hash(key);
    while(H->elem[addr]!=key)//冲突
    {
        addr=(addr+1)%HASHSIZE;//开放定址法 线性探测逆运算
        if(H->elem[addr]==NULLKEY||addr==Hash(key))//等于NULLKEY查找到最后一个，等于Hash(key)回到原点
          {
              return -1;
          }
    }
    return addr;
}
 void print(HashTable *H)
 {
     int i;
     for(i=0;icount;i++)
     {
         printf("%d\n",H->elem[i]);
     }
     printf("------------------------\n");
 }
int main()
{
    int i,j,result;
    HashTable H;
    int a[12]={8,6,9,13,17,50,62,95,83,11,46,25};
    InitHashTable(&H); //初始化哈希表
    for(i=0;i