C++递归法解决八皇后问题的超详细解答

博主初学C++数据结构与算法（清华大学出版社）第四版，由于程序清单5-2没有详细解答且代码不完整，思考了一个早上才恍然大悟，深感自己阅读代码以及写代码能力的不足，并在此记录，同时也希望也能帮到有需要的人！

 1、什么是八皇后问题？

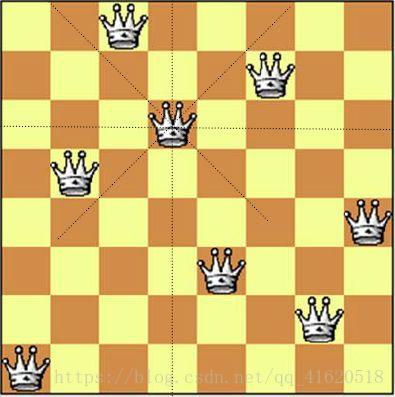
在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。例如下左图所示：

可见，每个皇后所处的位置，不在其他皇后的同行，同列，以及同一斜线上。

2、解决思路

       1）先考虑四皇后，即在4*4的棋盘格上放置4皇后，满足上述规则，进而在拓展至8皇后。

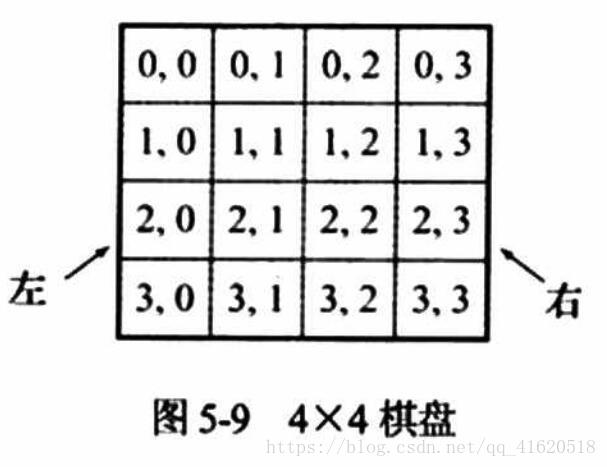
       2）我们一把4*4棋盘格的行列定义如下：

              

       3)最自然的实现方法是声明一个表示棋盘的4×4数组 board,其元素是0和1。1代表此位置可以放置皇后，而0则表示不可以。这个数组初始化为1,每当把一个皇后放在位置(r,c), board[r][c]就设置为0。同时,函数将所有不能放置棋子的位置均设置为0,即第r行和第c列上的所有位置,以及与(r,c)在同一条斜线上的所有位置。

       4)上图给出了4×4棋盘。注意图上指示“左”的斜线上所有位置的横竖坐标加起来为2,r+c=2这个数字与这条对角线相关。一共有7条左斜线,与它们相关的数分别是0到6。图上指示“右”的斜线上所有位置的横竖坐标之间的差值相同,r-c=-1,每条右斜线的这个值都不同。这样,给右斜线赋值为-3到3。左斜线使用的数据结构是一个下标从0到6的简单数组。对右斜线而言,其数据结构也是一个数组,但是数组的下标不能为负数。因此该数组具有7个元素,但是考虑到表达式r-c得到的负值,因此给r-c统一加上一个常数(norm),从而避免数组越界。

3、代码实现

     （建议大家把代码复制到VS中，运用快捷键方便理解代码：例如F12为转到定义，Alt+F12为速览定义）

#include 
using namespace std;

class ChessBoard {
public:
	ChessBoard();    // 8 x 8 chessboard;自定义构造函数
	ChessBoard(int); // n x n chessboard;带有参数的构造函数
	void findSolutions();
private:
	const bool available;
	const int squares, norm;//squares代表棋盘格的边长，norm的意义在2、(4)中有提到
	bool *column, *leftDiagonal, *rightDiagonal;//定义列，左斜线以及右斜线
	int  *positionInRow, howMany;//定义行以及方法的数量
	char m[10][10];//记录棋盘格
	void putQueen(int);
	void printBoard();
	void initializeBoard();
	void Delete();//释放new分配的动态内存
};

ChessBoard::ChessBoard() : available(true), squares(8), norm(squares - 1) {
	initializeBoard();
}
ChessBoard::ChessBoard(int n) : available(true), squares(n), norm(squares - 1) {
	initializeBoard();
}
void ChessBoard::initializeBoard() {
	register int i;//将整数i寄存器，目的使的运算更快
	column = new bool[squares];
	positionInRow = new int[squares];
	leftDiagonal = new bool[squares * 2 - 1];//左斜线的数目
	rightDiagonal = new bool[squares * 2 - 1];//右斜线的数目
	for (i = 0; i < squares; i++)
		positionInRow[i] = -1;//positionInRow是一个数组，i，即下标代表其行数，
							//positionInRow[i]储存的值为其列数
	for (i = 0; i < squares; i++)
		column[i] = available;//将每一列都设置为可以放置皇后的情况
	for (i = 0; i < squares * 2 - 1; i++)
		leftDiagonal[i] = rightDiagonal[i] = available;
	howMany = 0;
}
void ChessBoard::printBoard() {
	howMany++;//
	cout << howMany << " way is:" << endl;
	//为棋盘格赋值为1
	for (int i = 0;i != squares;i++) {
		for (int j = 0;j != squares;j++)
			m[i][j] = '1';
	}
	//将皇后的位置在棋盘格上用'*'标志出来
	for (int row = 0;row != squares;row++)
		m[row][positionInRow[row]] = '*';
	//打印棋盘格
	for (int i = 0;i != squares;i++) {
		for (int j = 0;j != squares;j++)
			cout << m[i][j];
		cout << endl;
	}
	cout << endl;
}

//具体见博客内容
void ChessBoard::putQueen(int row) {
	for (int col = 0; col < squares; col++) {
		if (column[col] == available &&
			leftDiagonal[row + col] == available &&
			rightDiagonal[row - col + norm] == available)
		{
			positionInRow[row] = col;
			column[col] = !available;
			leftDiagonal[row + col] = !available;
			rightDiagonal[row - col + norm] = !available;
			if (row < squares - 1)
				putQueen(row + 1);
			else printBoard();
			column[col] = available;
			leftDiagonal[row + col] = available;
			rightDiagonal[row - col + norm] = available;
		}
	}
}
void ChessBoard::Delete() {
	delete[]column;
	delete[]positionInRow;
	delete[]leftDiagonal;
	delete[]rightDiagonal;
}
void ChessBoard::findSolutions() {
	putQueen(0);
	cout << howMany << " solutions found.\n";
	Delete();
}
int main() {
	ChessBoard board(7);
	board.findSolutions();
	while (true)
	{

	}
	return 0;
}

4、代码详细解读

       1）这里重点介绍putQueen成员函数，其余函数相信大家在代码的注释可以看懂，不懂的可以在评论区回复我或者私信我，我会第一时间给大家答复。

       2）putQueen成员函数用了递归的方法。下面先给大家大概讲解一下递归算法。不知道大家有没有看过《盗梦空间》，个人感觉递归的算法就好像《盗梦空间》里进入梦境一样。正如下面的代码：

#include 
using namespace std;

double power(double x, unsigned int n) {
	if (n == 0)
		return 1.0;
	else
		return x * power(x, n - 1);
}

int main(){
	cout << power(5,3) << endl;
	while (true) {}
	return 0;
}

这段代码主要作用是计算x的n次幂。当要计算5^3时，函数power则会运行return x * power(x, n - 1);这个函数式。

       1）我们可以把power这个函数式想成是现实中在睡觉做梦一般（第一层梦境），然后再调用return x * power(x, n - 1);的位置，就好像是进入了下一层梦境一般（第二层梦境），来到了power(5,2)；

       2）在power(5,2)里（第二层梦境），此后又会再一次调用return 5 * power(5, 2 - 1)，在这个位置，又进入了下一层梦境（第三层梦境）。

       3）然而在这一层梦境中（第三层梦境）（power(5, 2 - 1)），我们找到了我们想要找到的东西，就是此时n=1，函数返回1.0，这个的意思就是power(5, 1)=1。找到了我们想要找的东西后，我们必须原路返回，不然就会被困在梦境中，不能脱身。

       4）此时我们将按照进来的位置原路返回到第二层梦境，即power(5,2)的return语句，在这里，我们将找到的东西power(5, 2-1)=1代入return 5 * power(5, 2 - 1)，得出power(5,2)=5;

       5）此后我们返回进入第二层梦境的地方，即第一层的return x * power(5, 3-1);的位置，power(5,2)=5代入便可找到最终解，power(5,3)返回125。

递归的好处就是代码看上去更直观一些，逻辑上的简单性以及可读性，其代价是降低了运算速度，这涉及到函数调用时栈帧的相关知识，在此不做过多讨论。

言归正传，回到putQueen的代码

void ChessBoard::putQueen(int row) {
	for (int col = 0; col < squares; col++) {
		if (column[col] == available &&
			leftDiagonal[row + col] == available &&
			rightDiagonal[row - col + norm] == available)
		{
			positionInRow[row] = col;
			column[col] = !available;
			leftDiagonal[row + col] = !available;
			rightDiagonal[row - col + norm] = !available;
			if (row < squares - 1)
				putQueen(row + 1);
			else printBoard();
			column[col] = available;
			leftDiagonal[row + col] = available;
			rightDiagonal[row - col + norm] = available;
		}
	}
}

0、先说明一下：row=0代表棋盘格的第一行，col=0时代表棋盘格的第一列，即[0,0]为第一行第一列。

1、首先col=0，row0=0，由于我们在initializeBoard函数里将column、leftDiagonal、rightDiagonal权初始为1，即可以放置皇后。

2、进入if结构，用positionInRow[0]记录下此时的列数，说明皇后放置在[0,0]，将第一列以及其斜线设置为不可放置状态。正如在{2、解决思路中的(4)}所述，此点的右斜线上的位置的r-c是常数，加上常数norm确保下标不为负数；此点的左斜线上的位置的r+c为常数，以此来确保位置的唯一性。

3、此后，由于row第一梦境进入到第二梦境，即putQueen(0+1)。

4、在第二梦境中，此时又是从col=0开始，但此时row=1，即皇后要在第二行找位置，此时由于在[0,0]的位置已经放置了皇后了，所以此时的column[0]，leftDiagonal[0]，rightDiagonal[3]都是不可访问的，这限制了此时皇后的col不能等于0,或1，在循环的作用下即等于2，如下图所示

5、同（2、），记录下此时的列数，设置不可放置状态。此时状态图为

6、同（3、）由于row第三梦境（即putQueen(1+1)）。

7、由上图可见，皇后只能放置在[2,1]处，而后记录下此时的列数，设置不可放置状态，进入第四梦境（即putQueen(2+1)）。

8、但是此时，我们可以得知，通过for循环是进入不了if条件里面的语句的，即找不到这个点，那么此时经过4次循环后，putQueen(2+1)运行完毕，但是此时函数将什么也不做。现在我们可以得知第四层梦境已经结束了，我们要返回上一层梦境了，即putQueen(2)，要注意，这层梦境的东西仅与这层梦境相关，不与上一层或者说下一层相关，就好比在putQueen(2)里，row就等于2，其他参数也是如此。

9、返回至第三梦境，putQueen(2)，则进行的是如下步骤：        

column[col] = available;
            leftDiagonal[row + col] = available;
            rightDiagonal[row - col + norm] = available;

这些步骤的目的将作用于我们在第三层里设置的不可放置状态，将他们全部设置为可放置状态。因为要是成功的话，其实此时row应该等于3，调用else里面的printBoard()函数。要是没有在调用的话，只有两种可能：一是下一层的尝试失败了，所以就要改变当层的放置情况，当然就要把已经设置为不可放置状态的reset。这种情况就是我们现在遇到的状况，可以在任一层梦境中实现。二是已经成功了，调用了else后，打印出了棋盘格，但将此次的不可放置状态reset，是想着寻找更多的方法，因此也需要reset。

9、当上述步骤完成的时候，切记切记，你以为就直接返回第二梦境了吗？大错特错！而是会在接着进行两次for循环，状态图如下

两次for循环分别为：一次col=2以及col=3的for循环，但我们都知道，这是不可能会被放置的位置的，所以当循环结束了，即putQueen(2)运行完毕，返回至第二梦境，即putQueen(1)；

10、返回至putQueen(1)时，将此次的不可放置状态reset，reset后进入col=3的循环，即在row=1时，将皇后放置在[1,3]，状态图如下，各位聪明的宝宝们肯定知道这样也是不行的，最终将会返回到第一层梦境

11、同理。reset，然后通过for循环将皇后放置在[0,1]上，然后进入下一层，通过for把皇后放在[1,3]上，[2,1]上，[3,3]上，就成功实现了第一种方法！如图：

12、接下来则在第四层梦境中，将row=3时的情况reset，然后是先进行一次col=3的for循环再返回至第三层！！！同样在第三层reset，然后在进行for循环尝试所有的可能！！！（不可遗漏）

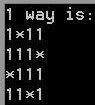
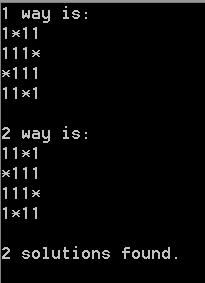
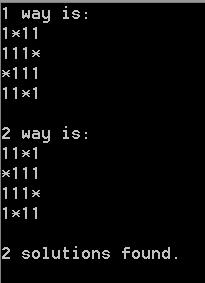
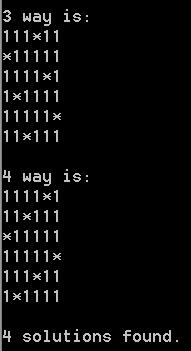
13、下面就是squares=4、5、6、8时的部分输出

squares=4：

squares=5：

squares=6：

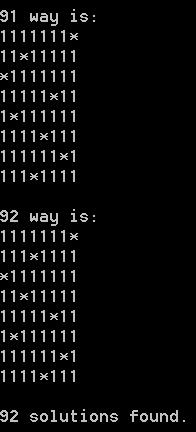
squares=8：