算法设计技巧: 广度优先搜索(BFS)
给定一个图 G = ( V , E ) G=(V,E) G=(V,E), 其中 V V V代表顶点的集合, E E E代表边的集合. 给定初始点 s ∈ V s\in V s∈V, 遍历图 G G G所有顶点一般有两种方法: 广度优先(Breadth-first-search)和深度优先(Depth-first-search). 本文介绍广度优先的思想和实现方式.
广度优先
如下图所示, 从 s s s开始, 由内向外逐层搜索, 顶点所在的 层数 代表了它与 s s s之间的 距离. 因此, 广度优先的特点是可以在遍历所有顶点 v ∈ V v\in V v∈V时计算 s s s和 v v v之间的最短距离(边数).
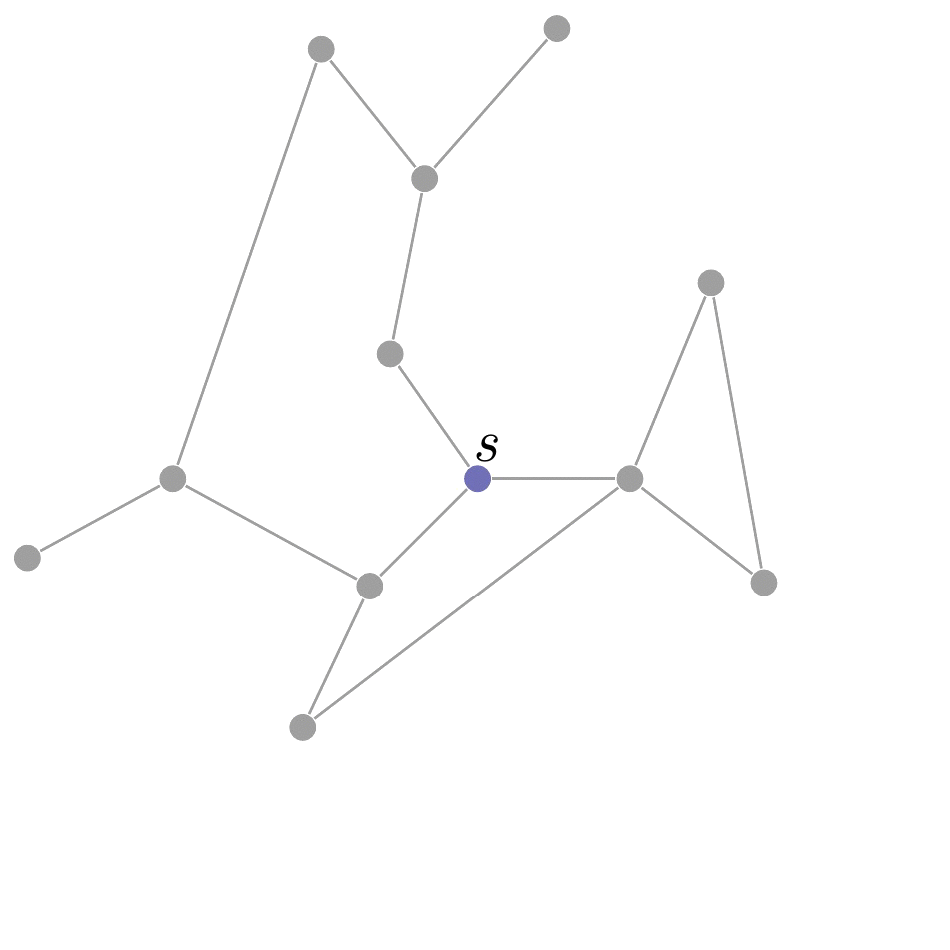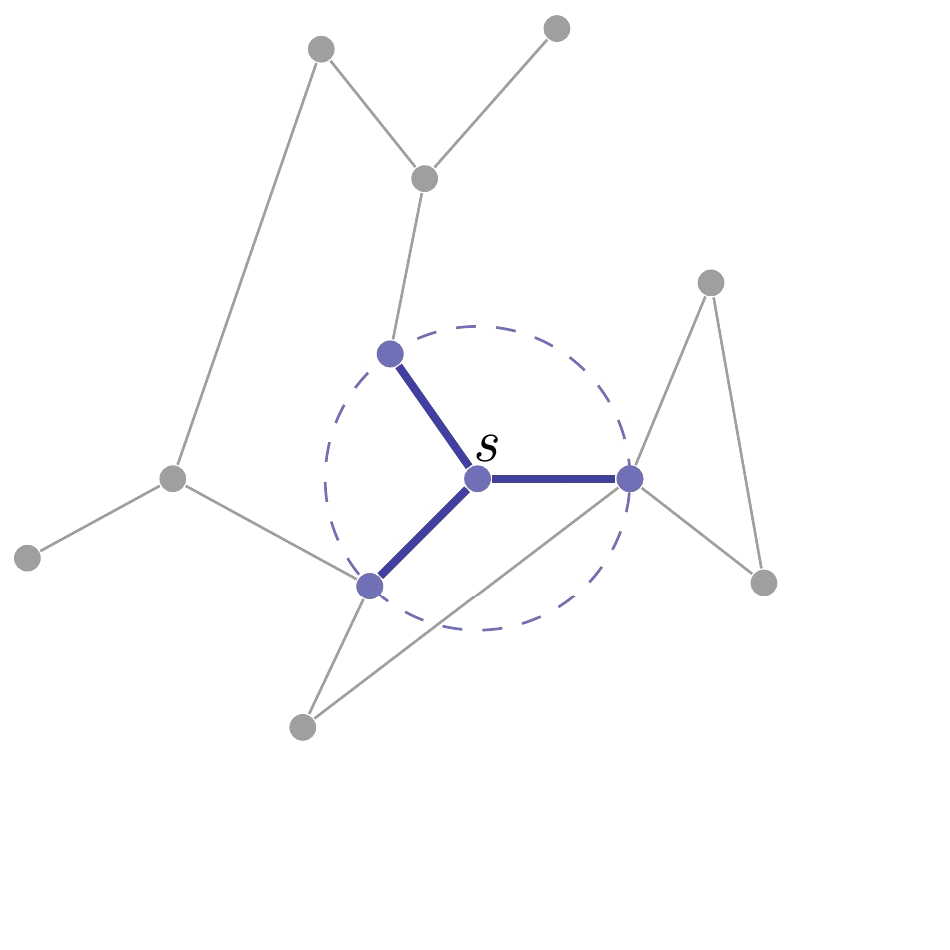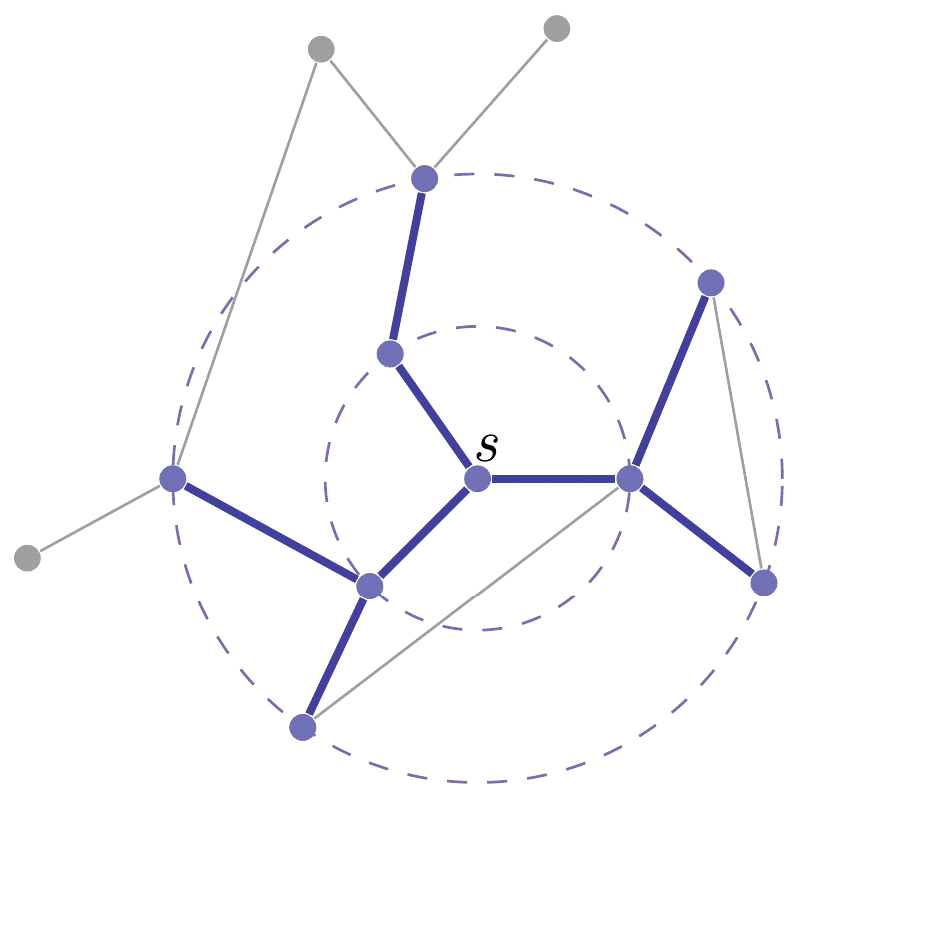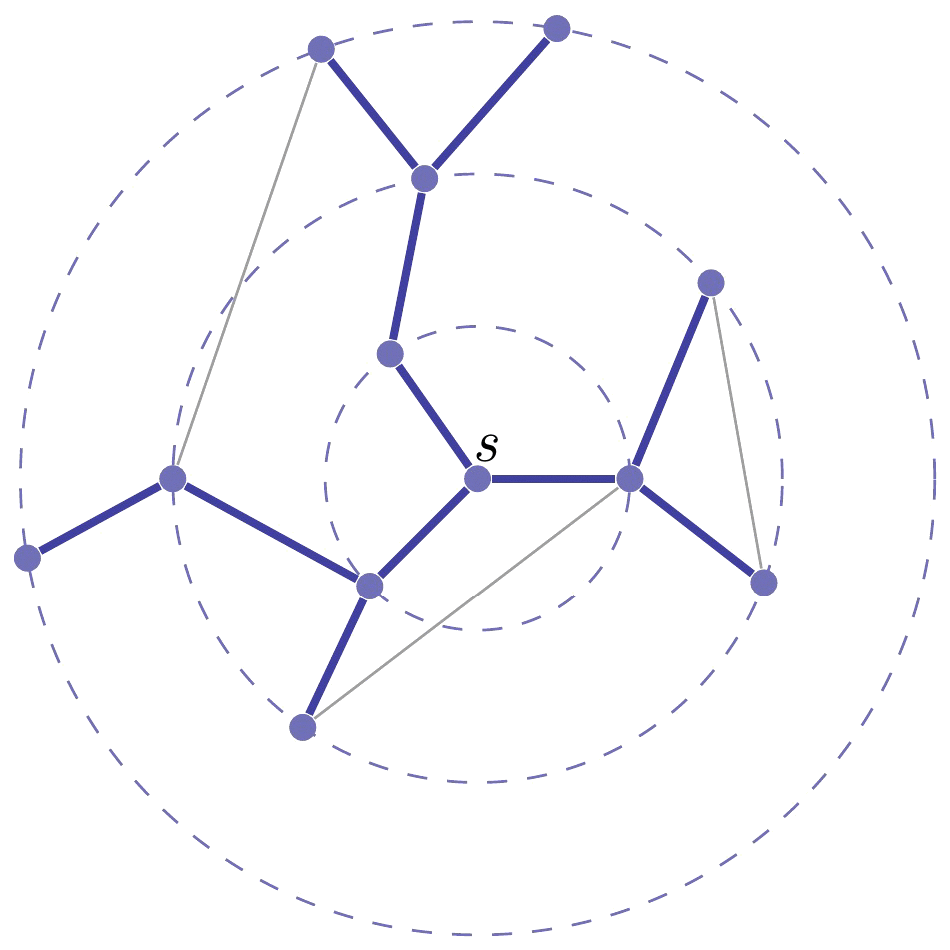
在搜索过程中, 我们用着色的方法对顶点进行分类:
- 白色: 未被搜索
- 灰色: 被搜索, 且存在一个邻接点未被搜索
- 黑色: 它及其所有邻接点被搜索
首先把 s s s加入队列(Queue), 且标记为灰色. 当队列不为空, 从队列中弹出一个顶点 u u u, 然后遍历与 u u u邻接的顶点: 标记为灰色并加入到队列中, 此时 u u u的所有顶点被访问到, 因此把 u u u标记为黑色. 当队列为空时所有点都标记为黑色时,算法停止, 即遍历完所有与 s s s连通的顶点.
Python实现
假设图 G G G的数据结构是邻接表.
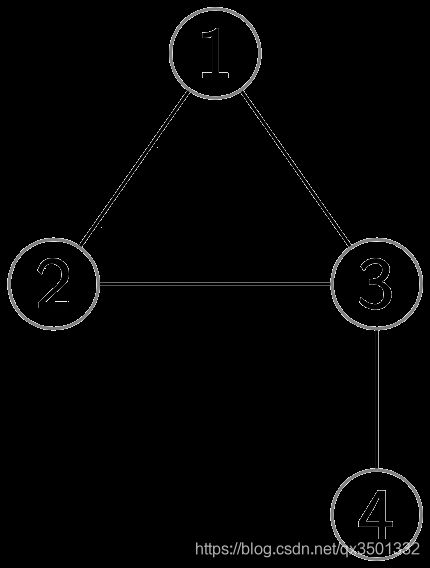
以上图为例, 它可以表示成如下形式:
1 → [ 2 , 3 ] 2 → [ 1 , 3 ] 3 → [ 1 , 2 ] 4 → [ 3 ] . \begin{aligned} & 1 \rightarrow [2, 3] \\ & 2 \rightarrow [1, 3] \\ & 3 \rightarrow [1, 2] \\ & 4 \rightarrow [3]. \\ \end{aligned} 1→[2,3]2→[1,3]3→[1,2]4→[3].
import math
class BFS(object):
""" Breadth-first-search.
得到搜索树和最短路(边权=1).
"""
def __init__(self, G, s):
"""
:param G: Graph, 数据结构为邻接表:
key = node index, value = list of adjacent node indices, e.g.,
{
0: [...] # node 0
1: [...] # node 1
...
}
:param s: 搜索的初始点的编号, int
"""
self._G = G
self._s = s
self._d = self._init_distances()
# colors
# white-未被发现
# gray-发现但未发现它所有邻接点
# black-发现它以及所有的邻接点
self._c = {v: 'white' for v in self._G.keys()}
# 记录搜索树
self._p = {} # key = node, value = parent
def _init_distances(self):
d = {v: math.inf for v in self._G.keys()}
d[self._s] = 0
return d
def run(self):
q = [self._s]
self._c[self._s] = 'gray'
while len(q):
u = q.pop(0)
# 考虑u的所有邻边(u, v)
for v in self._G[u]:
if self._c[v] == 'white':
self._d[v] = self._d[u] + 1
self._p[v] = u
self._c[v] = 'gray'
q.append(v)
self._c[u] = 'black'
完整代码
Remark. 更多关于广度优先搜索的应用可以参考文章: 用正六边形分割地图.