最小生成树-普利姆和克鲁斯卡尔算法

最小生成树主要是用于解决修路问题等类似问题，要将所有顶点连通，并且权值之和最小。

最小生成树

1. 给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为最小,这叫最小生成树
2. N个顶点，一定有N-1条边
   包含全部顶点
3. N-1条边都在图中
4. 求最小生成树的算法主要是普里姆算法和克鲁斯卡尔算法

普利姆算法

算法介绍

普利姆(Prim)算法求最小生成树，也就是在包含n个顶点的连通图中，找出只有(n-1)条边包含所有n个顶点的连通子图，也就是所谓的极小连通子图

普利姆的算法如下:

1. 设G=(V,E)是连通网，T=(U,D)是最小生成树，V,U是顶点集合，E,D是边的集合
2. 若从顶点u开始构造最小生成树，则从集合V中取出顶点u放入集合U中，标记顶点v的visited[u]=1
3. 若集合U中顶点ui与集合V-U中的顶点vj之间存在边，则寻找这些边中权值最小的边，但不能构成回路，将顶点vj加入集合U中，将边（ui,vj）加入集合D中，标记visited[vj]=1
4. 重复步骤②，直到U与V相等，即所有顶点都被标记为访问过，此时D中有n-1条边

其实，按照我个人的理解，可以简单概括为：对所有已经加入（已经访问过）的顶点，在它们的所有未访问过的边中找到权值weight最小的边，加入结果集，并标记边的另一个顶点为已访问过，一直循环这歌过程，直到加入了n-1条边。

代码

首先要有一个创建和存储图信息的类

class Graph:
    """
    图的构造类
    """
    def __init__(self, vertex_num):
        """
        :param vertex_num: 顶点的数量
        """
        self.vertex_num = vertex_num
        self.vertexs = None
        self.weights = None

    def create(self, vertexs, weights):
        """
        :param vertexs: 所有顶点集合
        :param weights: 边的邻接矩阵，二维数组
        :return:
        """
        self.vertexs = vertexs
        self.weights = weights

然后，开始我们的普利姆算法

class MinimumSpanningTree:
    """
     通过构建最小生成树，解决修路：要将所有顶点连通，并且使用的费用最低即权值之和最小
    """
    def import_graph(self, graph: Graph):
        self.graph = graph

    def prim(self, start):
        """
        利用普利姆算法构建最小生成树
        :param start:
        :return:
        """
        # 用于判断每个顶点是否已经访问的list
        visited = [False] * self.graph.vertex_num
        visited[start] = True

        for k in range(1, self.graph.vertex_num):
            min_weight = 10000
            i1 = -1
            i2 = -1

            # 对所有已经加入（已经访问过）的顶点，在它们的所有未访问过的边中找到权值weight最小的边，加入结果集，并标记为已访问过
            for i in range(self.graph.vertex_num):
                if not visited[i]:
                    continue
                for j in range(self.graph.vertex_num):
                    if (self.graph.weights[i][j] < min_weight) & (not visited[j]):
                        min_weight = self.graph.weights[i][j]
                        i1 = i
                        i2 = j
            visited[i2] = True
            print('%s -> %s : %d' % (self.graph.vertexs[i1], self.graph.vertexs[i2], min_weight))

测试图例

if __name__ == '__main__':
    # 普利姆算法测试
    graph = Graph(7)
    vertexts = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
    weights = [[10000, 5, 7, 10000, 10000, 10000, 2],
               [5, 10000, 10000, 9, 10000, 10000, 3],
                [7, 10000, 10000, 10000, 8, 10000, 10000],
                [10000, 9, 10000, 10000, 10000, 4, 10000],
                [10000, 10000, 8, 10000, 10000, 5, 4],
                [10000, 10000, 10000, 4, 5, 10000, 6],
                [2, 3, 10000, 10000, 4, 6, 10000]]
    graph.create(vertexts, weights)
    tree = MinimumSpanningTree()
    tree.import_graph(graph)
    tree.prim(0)

克鲁斯卡尔算法

算法介绍

克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。
基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路
具体做法：首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

这里其实最关键的就是两点：

1. 按照权值从小到大的顺序选择n-1条边
2. 选择的边不构成回路

步骤解析

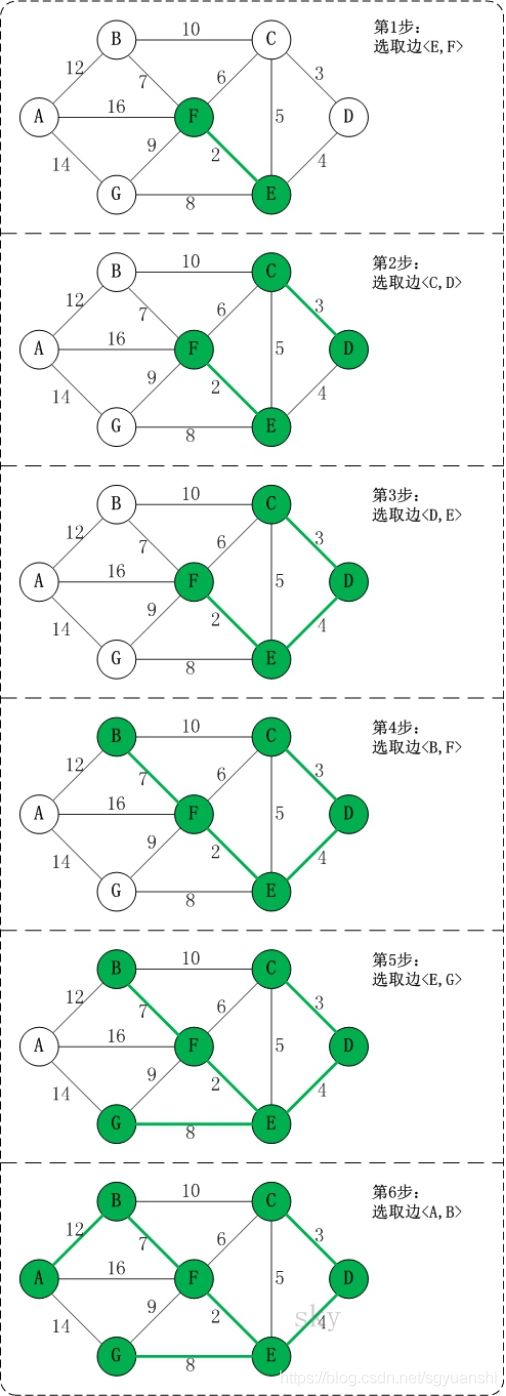
第1步：将边加入R中。
边的权值最小，因此将它加入到最小生成树结果R中。
第2步：将边加入R中。
上一步操作之后，边的权值最小，因此将它加入到最小生成树结果R中。
第3步：将边加入R中。
上一步操作之后，边的权值最小，因此将它加入到最小生成树结果R中。
第4步：将边加入R中。
上一步操作之后，边的权值最小，但会和已有的边构成回路；因此，跳过边。同理，跳过边。将边加入到最小生成树结果R中。
第5步：将边加入R中。
上一步操作之后，边的权值最小，因此将它加入到最小生成树结果R中。
第6步：将边加入R中。
上一步操作之后，边的权值最小，但会和已有的边构成回路；因此，跳过边。同理，跳过边。将边加入到最小生成树结果R中。

此时，最小生成树构造完成！它包括的边依次是：

回路

我们加入的边的两个顶点不能都指向同一个终点，否则将构成回路。

在将 加入到最小生成树R中之后，这几条边的顶点就都有了终点：

(01) C的终点是F。
(02) D的终点是F。
(03) E的终点是F。
(04) F的终点是F。

这里需要注意的是，只有当边加入连通了了之后，才能有所谓的终点

例如仅仅只有 加入后，像A、B这样的顶点是还没有终点，也可以认为终点是它们自己。

代码实现

def kruskal(self):
    """
    利用克鲁斯卡尔算法构建最小生成树
    :return:
    """
    ends = [0] * self.graph.vertex_num  # 用于存储每个顶点的终点

    edges = []  # 用于存储排序后的边
    # 开始进行排序
    # 遍历邻接矩阵，将边提取出来的同时插入edges，并保证有序
    visited = [False] * self.graph.vertex_num
    for i in range(self.graph.vertex_num):
        for j in range(self.graph.vertex_num):
            if visited[j]:
                continue
            if self.graph.weights[i][j] != 10000:
                index = len(edges)
                for n in range(len(edges)):
                    if self.graph.weights[i][j] < weights[edges[n][0]][edges[n][1]]:
                        index = n
                        break
                edges.insert(index, (i, j))
        visited[i] = True

    # 开始克鲁斯卡尔算法
    # 选取权值最小的n-1条不构成回路的边，即为最小生成树
    selects = []
    for edge in edges:
        if len(selects) > self.graph.vertex_num - 1:
            break
        # 首先判断是否构成回路
        end1 = self.get_end(edge[0], ends)
        end2 = self.get_end(edge[1], ends)
        if end1 == end2:
            continue
        elif end1 > end2:
            ends[end2] = end1  # 更新终点数组
            selects.append((self.graph.vertexs[edge[0]], self.graph.vertexs[edge[1]]))
        else:
            ends[end1] = end2
            selects.append((self.graph.vertexs[edge[0]], self.graph.vertexs[edge[1]]))
    print(selects)

def get_end(self, v, ends):
    """
    计算输入顶点的终点
    :param v:
    :param ends: 存储每个顶点的终点
    :return:
    """
    while ends[v] != 0:
        v = ends[v]
    return v

测试代码

graph = Graph(7)
vertexts = ['A', 'B', 'C', 'D', 'E', 'F', 'G']
weights = [[10000,  12, 10000, 10000, 10000,  16,  14],
[12,   10000,  110000, 10000, 10000,   7, 10000],
[10000,  110000,   10000,   3,   5,   6, 10000],
[10000, 10000,   3,   10000,   4, 10000, 10000],
[10000, 10000,   5,   4,   10000,   2,   8],
[16,   7,   6, 10000,   2,   10000,   9],
[14, 10000, 10000, 10000,   8,   9,   10000]]
graph.create(vertexts, weights)
tree = MinimumSpanningTree()
tree.import_graph(graph)
tree.kruskal()

欢迎关注同名公众号：“我就算饿死也不做程序员”。
交个朋友，一起交流，一起学习，一起进步。