算法：通过克鲁斯卡尔(Kruskal)算法，求出图的最小生成树

之前我给大家分享过用普利姆(Prim)算法来求出图的最小生成树(点我去看看)，今天我再给大家分享一个也是求图的最小生成树的克鲁斯卡尔(Kruskal)算法

克鲁斯卡尔(Kruskal)算法，就相当于先将图的所有边都拿出来，然后图就剩下所有顶点，没有一条边，所有顶点都是孤立的（所有顶点都不与其他任何顶点连通）。然后再将所有的边依据权重的大小，从小到大来排序，然后再尝试在图中加入所有的边（按照权重从小到大依次尝试）。如果该边加入后会生成环圈，比如A-B-C-A这样的环通路，则该边需要舍弃，反之则接受该边。当足够的边都尝试加入后并都得到了结果（接受还是舍弃），克鲁斯卡尔(Kruskal)算法即停止（可以判断接受边的数量，如果等于顶点数-1，则可以停止算法，因为现在的边已经"足够"了）。算法停止后，将所有接受的边保留，其他边舍弃，示例图即变成了最小生成树

本次实现克鲁斯卡尔(Kruskal)算法，我们也用以前的Prim算法的图：

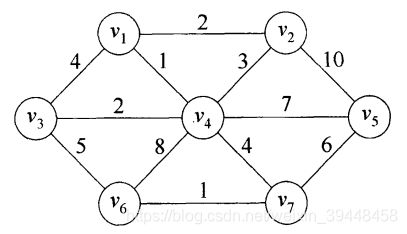
下面就是我用Java实现的克鲁斯卡尔(Kruskal)算法，求上面示例图的最小生成树，最后的结果应该是这样：

Edge.java：图的边的类，就是后面需要尝试加入的边：

/**
 * 图的边类
 * @Author: LiYang
 * @Date: 2019/10/26 22:13
 */
public class Edge implements Comparable<Edge>{

    //边的顶点1的下标
    public int vertex1;

    //边的顶点2的下标
    public int vertex2;

    //顶点之间的权重
    public int weight;


    /**
     * 无参构造方法
     */
    public Edge(){

    }

    /**
     * 全参数构造方法
     * @param vertex1 边的顶点1
     * @param vertex2 边的顶点2
     * @param weight 边的权重
     */
    public Edge(int vertex1, int vertex2, int weight) {
        this.vertex1 = vertex1;
        this.vertex2 = vertex2;
        this.weight = weight;
    }


    /**
     * 根据边的权重来排序
     * @param o
     * @return
     */
    public int compareTo(Edge o) {
        return this.weight - o.weight;
    }

}

KruskalAlgorithm.java：克鲁斯卡尔(Kruskal)算法类，包含该算法的实现过程，以及运算自定义图的方法，需导入上面的Edge类：

import java.util.*;

/**
 * 图的最小生成树之克鲁斯卡尔(Kruskal)算法：
 * 原理就是先将图的所有边去掉，然后再根据边的权重来排序，
 * 先尝试加入权重小的边，然后再加入权重大的边
 * 如果边加入后不生成环圈，则该边就可以加入，
 * 即为最后生成的最小生成树的组成边之一
 * 如果边加入后生成环圈，则该边不可加入，舍弃之
 * 将(顶点数-1)条边都这样加入过后，保留加入的边，即可组成最小生成树
 * @Author: LiYang
 * @Date: 2019/10/26 22:04
 */
public class KruskalAlgorithm {

    /**
     * 重要：根据克鲁斯卡尔(Kruskal)算法，尝试将边加入到生成树中
     * 如果返回true，则表示可以加入该边，不会生成圈，最终将加入该边
     * 如果返回false，则表示该边加入会生成圈，最终将舍弃该边
     * 注意：本方法采用的是广度优先遍历BFS方法遍历当前邻接矩阵，
     * 求出顶点1的连通范围，然后看顶点2是否在顶点1的连通范围之内
     * @param matrix 加入前的邻接矩阵
     * @param edge 即将加入的边
     * @return 是否加入了该边
     */
    public static boolean addEdge(int[][] matrix, Edge edge){
        //已经访问过的顶点集合（从顶点1开始）
        Set<Integer> visited = new HashSet<Integer>();

        //下一层次需要访问的顶点
        Set<Integer> nextBatch = new HashSet<Integer>();

        //先装入起始顶点（相当于求出起始顶点可以连通的所有顶点）
        nextBatch.add(edge.vertex1);

        //当下一层次的顶点集合不为空
        while (!nextBatch.isEmpty()){
            //将当前层次的顶点拿出
            Set<Integer> currentBatch = nextBatch;

            //下一层次顶点先清空
            nextBatch = new HashSet<Integer>();

            //遍历当前层次顶点，找出其下一层次的顶点
            for (Integer current : currentBatch){
                //取出当前顶点的数组（矩阵横向的数组）
                int[] currentRow = matrix[current];

                //找出可以到达的顶点下标
                for (int i = 0; i < currentRow.length; i++) {

                    //如果该点没有访问，且不是对角线和无穷大
                    if (!visited.contains(i) && currentRow[i] > 0
                            && currentRow[i] < Integer.MAX_VALUE){

                        //加入到下一层次顶点
                        nextBatch.add(i);
                    }
                }
            }

            //最后，将本层次的点，加入到已访问的集合中
            visited.addAll(currentBatch);
        }

        //所有已访问的点，都是与边的第一个顶点连通的，如果第二个顶点不在这个连通的集合中，
        //则表示该边的加入不会生成圈，即该边可以加入到最小生成树中，然后更新邻接矩阵。
        //否则就放弃该边，也不更新邻接矩阵
        if (!visited.contains(edge.vertex2)){

            //在邻接矩阵中加入该边（因为示例图是无向图，所以两边都要加上）
            matrix[edge.vertex1][edge.vertex2] = edge.weight;
            matrix[edge.vertex2][edge.vertex1] = edge.weight;

            //返回接受该边的结果
            return true;
        }

        //返回放弃该边的结果
        return false;
    }

    /**
     * 生成示例图的所有边的集合
     * 注意，刚开始可以不按权重升序加入边，但之后需要用
     * Collections.sort()方法让边以权重递增顺序排列
     * @return
     */
    public static List<Edge> initGraphEdges(){
        //边的集合，最后需要按照权重，从小到大排列
        List<Edge> edges = new ArrayList<Edge>();

        //加入示例图中所有的边
        //前两个参数是顶点的下标值，第三个参数是权重
        //顶点的下标值，与后面顶点名称字符串数组一一对应
        edges.add(new Edge(0, 3, 1));
        edges.add(new Edge(5, 6, 1));
        edges.add(new Edge(0, 1, 2));
        edges.add(new Edge(2, 3, 2));
        edges.add(new Edge(1, 3, 3));
        edges.add(new Edge(0, 2, 4));
        edges.add(new Edge(3, 6, 4));
        edges.add(new Edge(2, 5, 5));
        edges.add(new Edge(4, 6, 6));

        //如果上面边的加入是乱序的（没按权重从小到大依次加），就需要下面的操作了
        Collections.sort(edges);

        //返回按权重从小到大排列的边的集合
        return edges;
    }

    /**
     * 初始化邻接矩阵
     * 刚开始的时候，没有加入任何边，所有的顶点都是孤立的
     * @param vertexNum 顶点的数量
     * @return 初始化好了的邻接矩阵
     */
    public static int[][] initMatrix(int vertexNum){
        //定义邻接矩阵，正方形，边长为图顶点的个数
        int[][] matrix = new int[vertexNum][vertexNum];

        //初始化邻接矩阵
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix.length; j++) {
                if (i == j){

                    //对角线的权重为0
                    matrix[i][j] = 0;
                } else {

                    //初始化所有的顶点都不连通，即无穷大，用int最大值表示
                    matrix[i][j] = Integer.MAX_VALUE;
                }
            }
        }

        //返回所有顶点都不连通的初始邻接矩阵
        return matrix;
    }

    /**
     * 执行克鲁斯卡尔(Kruskal)算法
     * @param vertexNum 顶点的个数
     * @param edges 边的集合
     * @param vertexName 顶点名字的字符串数组
     */
    public static void kruskalAlgorithm(int vertexNum, List<Edge> edges, String[] vertexName){

        //得到初始化的矩阵
        int[][] matrix = initMatrix(vertexNum);

        //已接受的边的数量
        int acceptedEdgeNum = 0;

        //把边按权重从小到大，依次尝试加进去
        for (Edge currentEdge : edges){
            //如果加入的边已达顶点数-1，则已经组成最小生成树，算法结束
            if (acceptedEdgeNum == vertexNum - 1){
                break;
            }

            //将当前的边尝试加入，并返回是否成功
            boolean isAdded = addEdge(matrix, currentEdge);

            //如果当前边的加入被接受
            if (isAdded){
                //加入边的数量+1
                acceptedEdgeNum++;

                //输出成功信息
                System.out.println(String.format("边：(%s - %s)，权重：%d，动作：接受",
                        vertexName[currentEdge.vertex1], vertexName[currentEdge.vertex2],
                        currentEdge.weight));

            //如果当前边被舍弃
            } else {
                //输出失败信息
                System.out.println(String.format("边：(%s - %s)，权重：%d，动作：舍弃",
                        vertexName[currentEdge.vertex1], vertexName[currentEdge.vertex2],
                        currentEdge.weight));
            }
        }
    }

    /**
     * 运行克鲁斯卡尔(Kruskal)算法
     * 如果要运行自己的图，则需要更改三个地方：
     * 1、顶点数：int vertexNum
     * 2、图的边的集合，initGraphEdges() 方法的返回值，需要按权重排序
     * 3、顶点名称：String[] vertexName
     * @param args
     */
    public static void main(String[] args) {
        //示例图中的顶点数（如果自定义图，则需要改顶点数）
        int vertexNum = 7;

        //生成示例图中边的集合（如果自定义图，则需要改下面方法的返回值）
        List<Edge> edges = initGraphEdges();

        //顶点的下标与顶点名字对应的字符串数组（如果自定义图，这个也要改）
        String[] vertexName = new String[]{"V1", "V2", "V3", "V4", "V5", "V6", "V7"};

        //执行Kruskal(克鲁斯卡尔)算法，得到示例图的最小生成树
        kruskalAlgorithm(vertexNum, edges, vertexName);
    }

}

运行KruskalAlgorithm算法类的main方法求示例图的最小生成树，控制台显示：

边：(V1 - V4)，权重：1，动作：接受
边：(V6 - V7)，权重：1，动作：接受
边：(V1 - V2)，权重：2，动作：接受
边：(V3 - V4)，权重：2，动作：接受
边：(V2 - V4)，权重：3，动作：舍弃
边：(V1 - V3)，权重：4，动作：舍弃
边：(V4 - V7)，权重：4，动作：接受
边：(V3 - V6)，权重：5，动作：舍弃
边：(V5 - V7)，权重：6，动作：接受

我们看上面的输出结果，动作为"接受"的所有的边，就是最后组成最小生成树所需要的边。动作为"舍弃"的，则不是最小生成树所需要的边。我们将示例图中的所有边拿掉，然后加上以上所有的"接受"边，就求得示例图的最小生成树！下面的步骤是每有一条边被接受并加入之后的中间图，请大家根据控制台输出对比查看克鲁斯卡尔(Kruskal)算法逐渐生成最小生成树的过程（如果边被舍弃，那就说明该边加入形成了环，可以留意一下）：

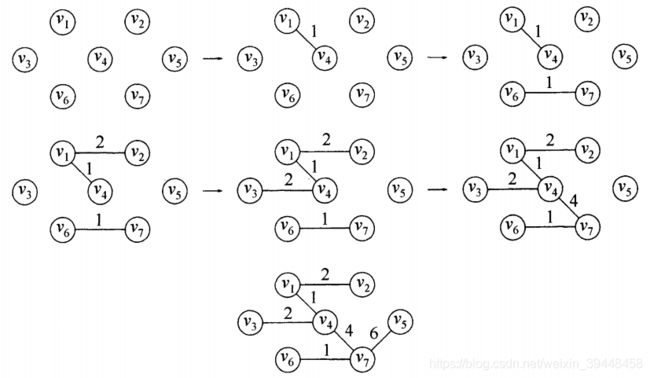
最后补充一点，克鲁斯卡尔(Kruskal)算法决定当前的边是否需要，可以用不相交集类来做。刚开始每个顶点都是独立的集合。选边的时候就表示边的两个顶点将变成一个集合，先用两个find方法查看是否是同一个集合。如果是，则代表两点已经连通，该边得舍弃。如果不是同一个集合，则这条边就可以要，然后将这两个顶点进行union操作。然后所有边的加入和舍弃就都清楚了。也可以在加入的边的数量等于顶点数-1的时候，终止算法，得出最小生成树。由于当时写博客的时候还没有接触不相交集类，所以用自己的方式来判断是否连通。以后如果有机会，我将用不相交集类，再实现一遍克鲁斯卡尔(Kruskal)算法