KNN之KD树实现
KNN之KD树
KNN是K-Nearest-Neighbors 的简称,由Cover和Hart于1968年提出,是一种基本分类与回归方法。这里主要讨论分类问题中的k近邻法。
•积极学习法 (决策树归纳):先根据训练集构造出分类模型,根据分类模型对测试集分类。•消极学习法 (基于实例的学习法):推迟建模,当给定训练元组时,简单地存储训练数据(或稍加处理),一直等到给定一个测试元。

KNN就是一种简单的消极学习分类方法,它开始并不建立模型,没有显式的学习过程。
•距离度量(邻居判定标准)•K值的选择(邻居数量)•分类决策规则(确定所属类别)
1、距离度量
闵氏距离不是一种距离,而是一组距离的定义(p是一个变参数)。
当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
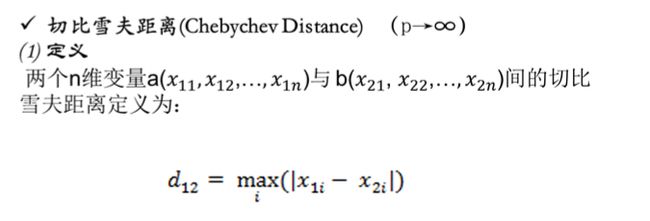
K值的选择
K值的选择影响:
1. 如果选择较小的K值,就相当于用较小的邻域中的训练实例进行预测。(极限情况K=1)
优点是“学习”的近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用。缺点是“学习”的估计误差会增大,对近邻点的实例点非常敏感。2. 如果选择较大的K值,就相当于用较大邻域中的训练实例进行预测。(极限情况K=N)
优点是可以减少学习的估计误差,对噪声不敏感。缺点是学习的近似误差会增大,与输入实例较远(不相似的)训练实例也会对预测器起作用,使预测发生错误。
K值的选择策略:
Step1:在实际应用中,K先取一个比较小的数值。
Step2:采用交叉验证法来逐步调整K值,最终选择适合该样本的最优的K值。
一般采用k为奇数,跟投票表决一样,避免因两种票数相等而难以决策。
常见的分类决策规则:
多数表决:少数服从多数。
由输入实例的k个邻近的训练实例中的多数类决定该实例的类。
加权表决:类似大众评审和专家评审。
根据各个邻居与测试对象距离的远近来分配相应的投票权重。
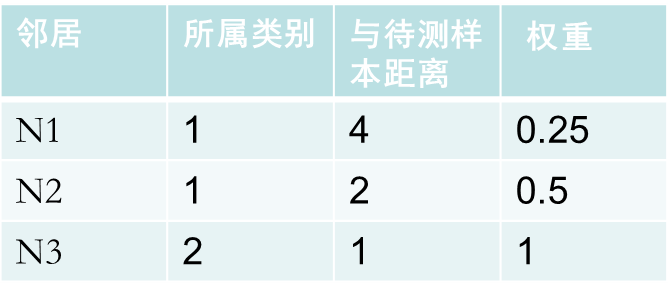
最简单的就是取两者距离之间的倒数,距离越小,越相似,权重越大,将权重累加,最后选择累加值最高类别属性作为该待测样本点的类别。
例:
类1: 0.25+0.5=0.75
类2:1
所以该待测样本属于类2
KNN算法:
线性扫描:对每一个待测样本点来说,都要对整个样本集逐一的计算其与待测点的距离,计算并存储好以后,再查找K近邻。
目的:减少计算量,减少存储量。
(1)采用特殊存储结构(例:kd树)
对样本集进行组织与整理,分群分层,尽可能将计算压缩到在接近测试样本邻域的小范围内,避免盲目地与训练样本集中每个样本进行距离计算,减少计算量。
(2)裁剪样本(例:压缩近邻算法,剪辑近邻法)
在原有样本集中挑选出对分类计算有效的样本,使样本总数合理地减少,以同时达到既减少计算量,又减少存储量的双重效果。
二、KD树的实现方法
Kd-树 其实是K-dimension tree的缩写,是对数据点在k维空间中划分的一种数据结构。其实,Kd-树是一种平衡二叉树。
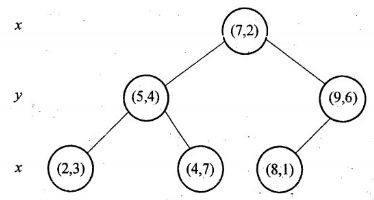
假设有六个二维数据点 = {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},数据点位于二维空间中。为了能有效的找到最近邻,Kd-树采用分而治之的思想,即将整个空间划分为几个小部分。六个二维数据点生成的Kd-树的图为:
KD树构建过程:
1.确定:split域=x。具体是:6个数据点在x,y维度上的数据方差分别为39,28.63,所以在x轴上方差更大,故split域值为x;
2.确定:Node-data=(7,2)。具体是:根据x维上的值将数据排序,6个数据的中值(所谓中值,即中间大小的值)为7,所以Node-data域位数据点(7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于split=x轴,即直线x=7;
3.确定:左子空间和右子空间。具体是:分割超平面x=7将整个空间分为两部分:x<=7的部分为左子空间,包含3个节点={(2,3),(5,4),(4,7)};另一部分为右子空间,包含2个节点={(9,6),(8,1)};
4. 递归:转1。对左子空间和右子空间内的数据重复根节点的过程就可以得到一级子节点(5,4)和(9,6),同时将空间和数据集进一步细分,如此往复直到空间中只包含一个数据点。
构建Kd-树的伪码为:
算法:构建Kd-tree
输入:数据点集Data_Set,和其所在的空间。
输出:Kd,类型为Kd-tree
1 if data-set is null ,return 空的Kd-tree
2 调用节点生成程序
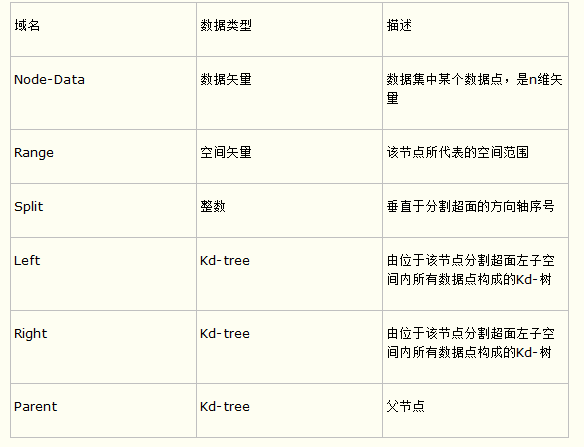
(1)确定split域:对于所有描述子数据(特征矢量),统计他们在每个维度上的数据方差,挑选出方差中最大值,对应的维就是split域的值。数据方差大说明沿该坐标轴方向上数据点分散的比较开。这个方向上,进行数据分割可以获得最好的分辨率。
(2)确定Node-Data域,数据点集Data-Set按照第split维的值排序,位于正中间的那个数据点 被选为Node-Data,Data-Set` =Data-Set\Node-data
3 dataleft = {d 属于Data-Set` & d[:split]<=Node-data[:split]}
Left-Range ={Range && dataleft}
dataright = {d 属于Data-Set` & d[:split]>Node-data[:split]}
Right-Range ={Range && dataright}
4 :left =由(dataleft,LeftRange)建立的Kd-tree
设置:left的parent域(父节点)为Kd
:right =由(dataright,RightRange)建立的Kd-tree
设置:right的parent域为kd。
KD树搜索
现查询点(2.1,3.1)
1.二叉树搜索:先从(7,2)点开始进行二叉查找,然后到达(5,4),最后到达(2,3),此时搜索路径中的节点为<(7,2),(5,4),(2,3)>。首先以(2,3)作为当前最近邻点,计算其到查询点(2.1,3.1)的距离为0.1414;
2.回溯查找:在得到(2,3)为查询点的当前最近点之后,回溯到其父节点(5,4)。首先判断该父节点,并不比当前最近点更近,所以无需替换。
接着判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以(2.1,3.1)为圆心,以0.1414为半径画圆,如下图所示。发现该圆并不和超平面y = 4交割,因此不用进入(5,4)节点右子空间中(图中灰色区域)去搜索;
3.回溯至根节点:最后,再回溯到(7,2),以(2.1,3.1)为圆心,以0.1414为半径的圆更不会与x = 7超平面交割,因此不用进入(7,2)右子空间进行查找。至此,搜索路径中的节点已经全部回溯完,结束整个搜索,返回最近邻点(2,3),最近距离为0.1414。
KNN分类性能
通常情况下,最近邻法(K=1)的错误率高于贝叶斯错误率。
其中P*代表的是贝叶斯误差率,由于一般情况下P*很小,因此又可粗略表示成:
对于KNN来说,当样本数量N→∞的条件下,k-近邻法的错误率要低于最近邻法,具体如图所示:
参考:
实验数据集:http://yunpan.cn/Q4MUPb6KAwejH 密码:f0bb
算法代码:http://yunpan.cn/Q4MUk276eL75g 密码:32ff