2020/3/19:目前正在已经大体通学了(超不牢固),所以现在想重新复习一遍各大结构,顺便做一份笔记总结一些解题套路
1、链表
链表的定义(来自维基百科):
在计算机科学中,链表作为一种基础的数据结构可以用来生成其它类型的数据结构。链表通常由一连串节点组成,每个节点包含任意的实例数据(data fields)和一或两个用来指向上一个/或下一个节点的位置的链接("links")。
链表与顺序表的区别(来自维基百科):
链表是一种常见的基础数据结构,是一种线性表,但是并不会按线性的顺序存储数据,而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储,链表在插入的时候可以达到 \(O(1)\) 的复杂度,比顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要 \(O(n)\) 的时间,而顺序表相应的时间复杂度分别是 \(O(logn)\) 和$ O(1)$。
链表的优缺点(来自维基百科):
使用链表结构可以克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。
链表最明显的好处就是,常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序,数据的访问往往要在不同的排列顺序中转换。而链表是一种自我指示数据类型,因为它包含指向另一个相同类型的数据的指针(链接)。链表允许插入和移除表上任意位置上的节点,但是不允许随机存取。
链表的类型(来自维基百科):
单向链表,双向链表以及循环链表。
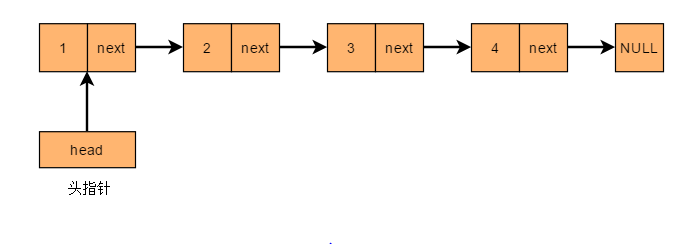
2、单向链表
单向链表的定义:
单向链表是链表类型中最为简单的一种,每个节点包含两个域,一个数据域(data),一个指针域(next)。单向链表的 next 节点指向下一节点,而尾节点的 next 节点为空。
单向链表节点定义:
struct Node
{
int val;
Node *next;
Node(): val(-1),next(nullptr) {}
};
单链表操作模板:
#include
using namespace std;
class MyLinkedList {
private:
struct ListNode
{
int val;
ListNode *next;
ListNode(int x) : val(x), next(nullptr) {}
};
ListNode* head;
public:
MyLinkedList() :head(nullptr) {}//构造函数初始化
//1.获得链表中第index个节点的值
int get(int index) {
if (index < 0)
return -1;
ListNode *p = head;//没有头结点的写法
//ListNode *p = head->next;//有头节点的写法
while (index != 0)
{
--index;
p = p->next;
}
return p->val;
}
//2.在链表头部插一个值为val的节点
void addAtHead(int val)
{
ListNode *p = new ListNode(val);
p->next = head;
head = p;//记得更换头结点
}
//3.在链表尾部添加一个值为val的节点
void addAtTail(int val)
{
ListNode *p = new ListNode(val);
//链表为空,直接将新节点作为头节点
if (head == nullptr)
{
head = p;
return;
}
ListNode *t = head;
while (t->next)
{
t = t->next;
}
t->next = p;
}
//4.在索引为index的节点之前添加值为val的节点
void addAtIndex(int index, int val) {
ListNode *node = new ListNode(val);
//1、index小于等于0,直接在头部插入节点
if (index <= 0)
{
addAtHead(val);
return;
}
ListNode* newNode = new ListNode(val);
ListNode* p = head;
while (index != 0)
{
p = p->next;
--index;
}
newNode->next = p->next;
p->next = newNode;
}
//5.删除索引为index的节点
void deleteAtIndex(int index) {
//1、index为0,我们直接删除head节点
if (index == 0 && head != nullptr)
{
ListNode *del = head;
head = head->next;
delete del;
return;
}
int i = 0;
ListNode* p = head;
//删除索引为index的节点,我们需要找到它的前驱节点p,p->next为需要删除节点
while (p&&i < index - 1)
{
p = p->next;
i++;
}
//2、index超过链表范围,删除失败
if (!p)return;
//3、index的位置合法,我们找到需要删除的p->next节点
if (p->next)
{
ListNode *del = p->next;
p->next = del->next;
delete del;
}
}
//6.链表长度
int length() {
int i = 0;
ListNode *p = head;
while (p) {
i++;
p = p->next;
}
return i;
}
//7.清空链表
void clear() {
ListNode *del = nullptr;
while (head) {
del = head;
head = head->next;
delete del;
}
}
};
int main()
{
MyLinkedList mlf;
mlf.addAtIndex(0, 10);
mlf.addAtIndex(0, 20);
mlf.addAtIndex(1, 30);
for (int i = 0; i < mlf.length(); ++i) {
cout << mlf.get(i) << " ";
}
cout << endl;
mlf.clear();
cout << mlf.length() << endl;
system("pause");
} 707. 设计链表
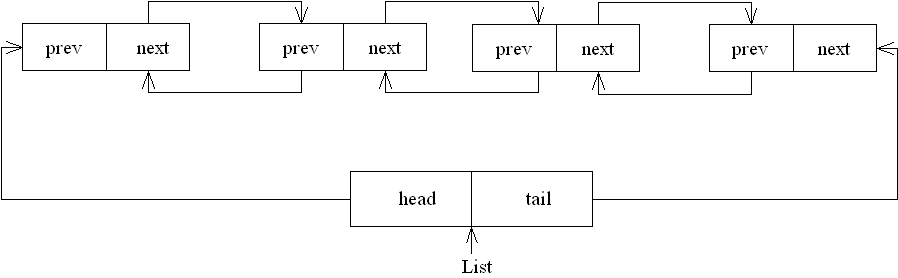
3、双向链表
双向链表的定义:
双向链表是一种更为复杂的链表,每个节点包含三个域,一个数据域(data)和两个指针域(prev、next),其中数据域存放节点的数值,prev 指向该节点的前一个节点,next 指向该节点的后一个节点。
双向链表节点的定义:
struct ListNode
{
int val;
ListNode *next,*prev;
ListNode(int x):val(x),next(nullptr),prev(nullptr){}
};
双向链表的模板:
#include
using namespace std;
class List
{
private:
struct ListNode
{
int val;
ListNode* prev, *next;
ListNode(int x): prev(nullptr),next(nullptr),val(x) {}
};
private:
ListNode *head, *tail;//设立尾节点,便于循环操作
int size = 0;
public:
List() :size(0), head(nullptr), tail(nullptr){} //构造函数初始化
//1.获得索引为index的节点值
int get(int index)
{
if (index < 0)
return -1;
ListNode *p = head;
while (index)
{
index--;
p = p->next;
}
return p->val;
}
//2.在头部插入值为val的新节点
void addAtHead(int val)
{
if (head == nullptr)
{
//尾节点为空,那么头节点也为空,然后首尾节点都为新节点
head = new ListNode(val);
tail = head;//记得将tail连起head
}
else
{
ListNode * newNode = new ListNode(val);
newNode->next = head;
head->prev = newNode;
head = newNode;
}
++size;
}
//3.在尾部插入值为val的新节点
void addAtTail(int val)
{
if (tail != nullptr) {
ListNode *node = new ListNode(val);
node->prev = tail;
tail->next = node;
tail = node;
}
else {//尾节点为空,那么头节点也为空,然后首尾节点都为新节点
tail = new ListNode(val);
head = tail;
}
++size;
}
//4.在index之前添加值为val的新节点
void addAtIndex(int index, int val)
{
//首先排除三种特殊情况的index,然后剩下来的index肯定在链表内
if (index <= 0)
{
addAtHead(val);
return;
}
if (index == size)
{
addAtTail(val);
return;
}
if (index > size)return;
ListNode *newNode = new ListNode(val);
ListNode *p = head;
while (index)
{
--index;
p = p->next;
}
newNode->next = p->next;
newNode->prev = p;
p->next = newNode;
size++;
}
//5.删除索引为index的节点
void deleteAtIndex(int index)
{
if (!head)return;
if (index == 0)
{
ListNode *del = head;
head = head->next;
if (head)
{//链表有2个以上节点
head->prev = nullptr;
}
else
{//链表只有一个节点,将尾部制空
tail = nullptr;
}
delete del;
size--;
return;
}
if (index == size - 1)
{
ListNode *del = tail;
tail = tail->prev;
//注意这里不用处理tail为空,因为tail为空的话,那么链表只有单个节点
//然而单个节点只能删除0号节点,只有index为0时才能删除,前面已经处理过了index为0的情况了,所以这里不在处理
if (tail)
{
tail->next = nullptr;
}
delete del;
size--;
return;
}
ListNode *del = head;
while (index)
{
--index;
del = del->next;
}
del = del->next;
del->prev->next = del->next;
delete del;
--size;
}
//6.获得链表的长度
int length() {
return size;
}
//7.清空链表
void clear()
{
//从尾节点不断删除
for (int i = size - 1; i >= 0; --i) {
deleteAtIndex(i);
}
}
};
int main() {
List mls;
mls.addAtHead(100);
mls.addAtTail(3);
mls.addAtIndex(1, 2);
for (int i = 0; i < mls.length(); ++i) {
cout << mls.get(i) << " ";
}
cout << endl;
mls.deleteAtIndex(1);
for (int i = 0; i < mls.length(); ++i) {
cout << mls.get(i) << " ";
}
cout << endl;
mls.clear();
cout << mls.length() << endl;
} 4、环形链表
环形链表的定义:
循环链表中, 首节点和末节点被连接在一起。这种方式在单向和双向链表中皆可实现。要转换一个循环链表,你开始于任意一个节点然后沿着列表的任一方向直到返回开始的节点。再来看另一种方法,循环链表可以被视为 “无头无尾”。这种列表很利于节约数据存储缓存, 假定你在一个列表中有一个对象并且希望所有其他对象迭代在一个非特殊的排列下。
说明:
关于环形链表的基本代码实现,我就不写了,因为用到的也比较少,大家有兴趣可以在单链表或者双链表的基础上将首尾节点连接在一起就好了。
5、习题解析
5.1、链表中的双指针技巧
19. 删除链表的倒数第N个节点:老实用快慢指针,快指针先走n步,然后快慢一起走,直到快指针走到最后,要注意的是可能是要删除第一个节点,这个时候可以直接返回head -> next
86. 分隔链表:巧妙的设立双链表Before_Link ,After_Link分别存储比x小 比x大的节点,最后尾首相连
92. 反转链表 I-I
109.有序链表转换二叉搜索树
141.环形链表:中规中矩的快慢指针,一旦链表有环的话快慢指针必定有一时刻会相等
142. 环形链表 II:最开始做的时候发现可以直接第一步套用No.141的代码,然后fast slow(重新赋head)各走一步相遇点为环入口。然后另一种解法是通过hash表,一旦出现表中存在的节点即可返回
143.重排链表
160. 相交链表:设链表A的长度为a+c,链表B的长度为b+c,a为链表A不公共部分,b为链表B不公共部分,c为链表A、B的公共部分 。将两个链表连起来,A->B和B->A,长度:a+c+b+c=b+c+a+c,若链表AB相交,则a+c+b与b+c+a就会抵消,它们就会在c处相遇;若不相交,则c为nullptr,则a+b=b+a,它们各自移动到尾部循环结束,即返回nullptr
206.反转链表
234.回文链表
876.链表的中间节点
5.2、链表排序问题
147.对链表进行插入排序
148.排序链表
5.3、链表经典题目
2.两数相加
21.合并两个有序链表
23.合并K个排序链表
24.两两交换链表中的节点
25.K个一组翻转链表
61.旋转链表
82.删除排序链表中重复元素Ⅱ
83.删除排序链表中重复元素
138.复制带随机指针的链表
203.移除链表元素
430.扁平化多级双向链表:
445.两数相加Ⅱ
725.分隔链表
817.链表组件:
1171.从链表中删去总和值为零的连续节点
注:如果大家觉得有用,不妨点个赞呗,嘿嘿!
