【算法】欧几里得算法(辗转相除法)简易证明
题目来源
近来看到书籍《算法图解》里面的一个例子:
假设你是农场主,有一块土地,你要将这块地均匀地分为方块,且分出来的分块要尽可能的大。
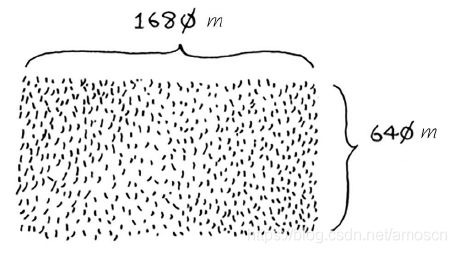
书中并未给出的解答过程就是用的欧几里得算法,具体证明过程无,我自己画了个图方便理解。
步骤:
- 从这块地
1680x640中划出两个640x640的方块,剩下的土地使用同样的计算方法:适用于剩余小块地的最大方块,也是适用于整块地的最大方块 - 从剩余的(1680-2*640=400)
640x400的方块中,划出一块400x400 - 从剩余的(640-400=240)
400x240的方块中,划出一块240x240 - 从剩余的(400-240=160)
240x160的方块中,划出一块160x160 - 从剩余的(240-160=80)
160x80的方块中,划出一块80x80,剩余同样是80x80(划出那块的n倍,此处n=1),结束
问题在哪里呢? 问题就出在:适用于剩余小块地的最大方块,也是适用于整块地的最大方块 !!??
证明过程
上面的整个计算过程实际上也是计算A,B两个数值的最大公约数(Greatest Common Divisor:记作符号gcd)的过程, 理解了这句话才好进行后面的推断过程。
示例
g c d ( 1680 , 640 ) = g c d ( 640 , 400 ) = g c d ( 400 , 240 ) = g c d ( 240 , 160 ) = g c d ( 160 , 80 ) = g c d ( 80 , 0 ) = 80 ; gcd(1680, 640) = gcd(640, 400) = gcd(400, 240) = gcd(240, 160) = gcd(160, 80) = gcd(80, 0) = 80 ; gcd(1680,640)=gcd(640,400)=gcd(400,240)=gcd(240,160)=gcd(160,80)=gcd(80,0)=80;
假设:
A = P × B + Q , ( P , Q 为 正 整 数 ) ; A = P×B+Q,(P, Q为正整数); A=P×B+Q,(P,Q为正整数);
现在我们需要证明为何 :
g c d ( A , B ) = g c d ( B , A − B ) = g c d ( B , A − n B ) = g c d ( Q , B ) , ( n 为 使 得 n B ≤ A 的 任 意 正 整 数 ) ; gcd(A, B) = gcd(B, A-B)=gcd(B, A-nB) = gcd(Q,B),(n为使得nB≤A的任意正整数); gcd(A,B)=gcd(B,A−B)=gcd(B,A−nB)=gcd(Q,B),(n为使得nB≤A的任意正整数);
理解算法
证明gcd(A,0)=A, gcd(0,B)=B
- 因为A×1=A; 能整除A的最大约数是A:A÷A=1
- 因为对于任意整数C,都有C×0=0;可以得出0也可以整除A:0÷A=0
- 所以A和0的最大公约数就是A
证明B同理;
假设A-B=C; 现在证明gcd(A,B)也可以整除C:
因为:gcd(A,B)是A,B的最大公约数
所以:
1.必定存在一个数整数X,使得X×gcd(A,B)=A
2.必定存在一个数整数Y,使得Y×gcd(A,B)=B
根据A-B=C;于是有
X × g c d ( A , B ) − Y × g c d ( A , B ) = C ; X×gcd(A,B) - Y×gcd(A,B) = C; X×gcd(A,B)−Y×gcd(A,B)=C;
也即
( X − Y ) × g c d ( A , B ) = C ; (X-Y)×gcd(A,B) = C; (X−Y)×gcd(A,B)=C;
于是:gcd(A,B)也可以整除C
根据A-B=C;现在证明gcd(B,C)也可以整除A:
因为:gcd(B,C)是B,C的最大公约数
所以:
1.必定存在一个数整数S,使得S×gcd(B,C)=B
2.必定存在一个数整数T,使得T×gcd(B,C)=C
根据A-B=C;于是有 A=B+C
S × g c d ( B , C ) + T × g c d ( B , C ) = A S×gcd(B,C) + T×gcd(B,C)= A S×gcd(B,C)+T×gcd(B,C)=A
也即
( S + T ) × g c d ( B , C ) = A (S+T)×gcd(B,C)= A (S+T)×gcd(B,C)=A
于是:gcd(B,C)也可以整除A
根据目前已经证明的:
gcd(A,B)也可以整除C- 命名为已证01gcd(B,C)也可以整除A- 命名为已证02
重点:
因为gcd(A,B)可以整除B(根据定义)和C(根据已证01),则gcd(A,B)是B和C的公约数,gcd(B,C)也可以整除B和C,并且gcd(B,C)是B和C的最大公约数,那么可以得出:
gcd(B,C)一定是大于或者等于gcd(A,B) - 命名为
已证03。
因为gcd(B,C)可以整除A(根据已证02)和B(根据定义),则gcd(B,C)是A和B的公约数,gcd(A,B)也可以整除A和B,并且gcd(A,B)是A和B的最大公约数,那么可以得出:
gcd(A,B)一定是大于或者等于gcd(B,C) - 命名为
已证04;
在根据已证03和已证04(如果a≥b并且b≥a,那么a=b):
g c d ( A , B ) = g c d ( B , C ) = g c d ( B , A − B ) = g c d ( A − B , B ) ; gcd(A,B) = gcd(B,C) =gcd(B,A-B) =gcd(A-B,B) ; gcd(A,B)=gcd(B,C)=gcd(B,A−B)=gcd(A−B,B);
再根据上面得出的结论gcd(A,B) = gcd(A-B,B) 可以得出:
g c d ( A , B ) = g c d ( A − B , B ) = g c d ( A − B − B , B ) = g c d ( A − 2 B , B ) = . . . = g c d ( A − n B , B ) , ( n B ≤ A ) ; gcd(A,B) = gcd(A-B,B) = gcd(A-B -B,B) = gcd(A-2B,B) = ... =gcd(A-nB,B),(nB≤A); gcd(A,B)=gcd(A−B,B)=gcd(A−B−B,B)=gcd(A−2B,B)=...=gcd(A−nB,B),(nB≤A);
因为之前的假设:
A = P × B + Q ; A = P×B+Q; A=P×B+Q;
这里我们令n = P
g c d ( A , B ) = g c d ( P × B + Q , B ) = g c d ( P × B + Q − n B , B ) = g c d ( Q , B ) = g c d ( B , Q ) ; gcd(A, B) = gcd(P×B+Q, B) = gcd(P×B+Q - nB, B) = gcd(Q , B) = gcd(B , Q) ; gcd(A,B)=gcd(P×B+Q,B)=gcd(P×B+Q−nB,B)=gcd(Q,B)=gcd(B,Q);
得证!
参考
https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-euclidean-algorithm