OO第三单元作业总结

一、JML理论基础

　　JML是用于对Java程序进行规格化设计的一种表示语言，是对一种行为接口规格语言。通过它，可以完整的描述这个接口的行为，需要做到对于这个接口（方法）或者类型外部的内容的完整定义。

　　JML有两种主要用法：1.开展规格化设计，这样的话对于代码实现人员来说是莫大的福利。2.针对已有的代码实现，书写对应的规格，从而提高代码的可维护性。

描述关键字	含义
normal_behavior	正常行为
exceptional_behavior	异常行为
requires	前置条件
ensures	结束行为的后置条件
\result	方法执行后的返回值
\old(x)	x在方法执行前的值
\forall	全程量词
\exists	存在量词
\sum	求和
\max	求极大值
\min	求极小值
assignable	可以改变的数据
&& 、||、==、==>、<==>	与、或、相等、蕴含、互蕴含
invariant	不变式，指在所有可见状态下，都要满足的性质
constraint	状态变化的约束
signals(e)	异常行为时，抛出异常e

　　下面给出几个方法的JML规格及其实现。

 1 /*@ ensures \result == (people.length == 0? 0 : 
 2   @          ((\sum int i; 0 <= i && i < people.length; people[i].getAge()) / people.length));
 3   @*/
 4 public /*@pure@*/ int getAgeMean();
 5 ​
 6 //这个getAgeMean方法要求我们对于people数据容器中的所有age求平均，然后将其返回。
 7 ​
 8 ​
 9 /*@ public normal_behavior
10       @ assignable \nothing;
11       @ ensures \result == (\exists int i; 0 <= i && i < acquaintance.length; 
12       @                     acquaintance[i].getId() == person.getId()) || person.getId() == id;
13       @*/
14     public /*@pure@*/ boolean isLinked(Person person);
15 ​
16 //这个isLinked方法，需要我们判断参数person.getId是否与自身id相等，或与acquaintance中的id相等，最后将比较结果返回
17 ​
18 /*@ public normal_behavior
19       @ requires !(\exists int i; 0 <= i && i < people.length; people[i].equals(person));
20       @ assignable people, money;
21       @ ensures people.length == \old(people.length) + 1;
22       @ ensures money.length == people.length;
23       @ ensures (\forall int i; 0 <= i && i < \old(people.length); 
24       @         (\exists int j; 0 <= j && j < people.length; 
25       @         people[j] == \old(people[i]) && money[j] == \old(money[i])));
26       @ ensures (\exists int i; 0 <= i && i < people.length; people[i] == person && money[i] == 0);
27       @ also
28       @ public exceptional_behavior
29       @ signals (EqualPersonIdException e) (\exists int i; 0 <= i && i < people.length; 
30       @                                     people[i].equals(person));
31       @*/
32     public void addPerson(Person person) throws EqualPersonIdException;
33 ​
34 //这个addPerson方法，需要我们做几件事，首先判断是否在people中已经存在参数person，若存在则抛出异常EqualPersonIdException，如果不存在，则需要满足以上几点：
35　//1.people数组size比原来大1 2.money数组与更新后people数组size相等 3.原来在people和money里面的元素在新的people和money数组中都必须能找得到 
36   //4.新的元素也能在这两个数组更新后被找到。（简单的来说就是把person加到数组中）

 

　　我们可以看到，其实JML规格理解起来并不难，就是用离散数学的方法严谨地表达一个接口的行为，只要有离散数学的一部分知识，熟悉语法之后读起来就不难。

 

二、SMT Solver的部署与验证

 

　　我使用的是z3，但是z3并不能很好的支持太过于复杂的JML逻辑检查，所以我写了两个较为简单的方法进行测试。

 

 1 public class TestSMT {
 2     public static void main(String[] args) {
 3         System.out.println(Test.add(250, 520));
 4         System.out.println(Test.div(1, 2));
 5     }
 6     
 7     //@ensures \result == a + b;
 8     public int add(int a, int b) {
 9         return a + b;
10     }
11 ​
12     //@ensures \result == a % b;
13     public int mod(int a, int b) {
14         return a % b;
15     }
16 }
17 ​

 

　　通过测试我们可以得到，一条INVALID信息，他告诉我们mod存在不完整的地方，因为除法取余会出现除0的情况。

 

三、JMLUnitNG的部署与测试

 

　　JMLUnitNG同样不支持拥有全称量词和存在量词的关键词，所以本次测试我只选取了作业中两个很简单的方法。

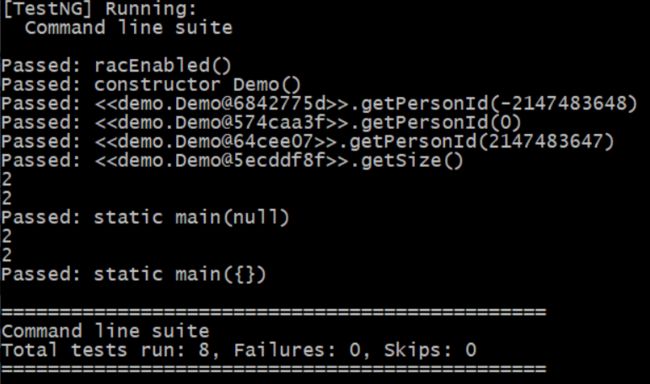
 1 package demo;
 2 import java.util.ArrayList;
 3 public class TestJML {
 4     public ArrayList peopleId = new ArrayList();
 5     public static void main(String[] args) {
 6          TestJML test = new TestJML();
 7          test.peopleId.add(1);
 8          test.peopleId.add(2);
 9          int a = test.getSize();
10          System.out.println(a);
11          int b = test.getPersonId(1);
12          System.out.println(b);
13     }
14     // @ public normal_behaviour
15     // @ requires index >= 0 && index < size();
16     // @ assignable \nothing;
17     // @ ensures \result == peopleId.get(index);
18     public   /*@pure@*/ int getPersonId(int id) {
19         if (id < 0 || id >= getSize()) {
20             return -1;
21          }
22          return peopleId.get(id);
23     }
24     // @ public normal_behaviour
25     // @ ensures \result = peopleId.size();
26     public /*@pure@*/ int getSize(){
27         return peopleId.size();
28     }
29 }

 

　　在自动生成测试文件之后，运行可以得到结果。

 

四、程序分析与设计策略

第一次作业

　　第一次作业可以说只要读懂了JML规格就基本上能写对。只有一个方法需要提一下，就是isCircle方法。这个方法是判断在图里的两个人之间是否存在通路。我们可以使用的方法很多，比如dfs，bfs还有并查集。第一次作业中，我是用的是bfs广度搜索。

第二次作业

　　第二次作业增加了组（多人组成）的数据查询，比如查询组内年龄平均，查询组内年龄方差，查询组内合集Value值等等。

　　这些查询按照规格来写的话其实非常简单，就是一个循环或者二重循环就能解决。但是考虑到数据量和CPU时间的限制，我们应该维护好我们已经算出来的这些量，或者是说，我们一开始就要计算，每增加一个人就更新一次，或者是每需要访问一次，就更新一次，不需要访问的时候就将没有加入到更新的people单独记录下来。这样大大降低了所需的时间。

第三次作业

　　本次作业的难点我认为在于两个方法：minpath和stronglinked，需要注意的还有blockSum。

　　对于blockSum方法，我们通过阅读JML规格不难发现，这是查找图中连通块的个数。由于我在第三次作业中将isCircle改为了并查集，所以处理这个方法十分的方便。

　　对于minPath方法，我们可以直接使用迪杰斯特拉求最短路经算法，但是要注意的是，由于数据量较为庞大，如果不做优化，每一次都需要在结构中寻找最短的那条路来更新的话，时间上没有保证。所以我采用了优先队列PriorityQueue的方式，或者说是堆优化的方式来处理，这样就不用每次遍历寻找最小值了。事实也证明，使用不优化的dij会导致两到三个点超时。

　　对于Stronglinked方法，这里分析两种算法。

　　首先是一个较为简单，容易理解的算法。我们知道如果两个点点双连通，那么至少就会有两条路连通这两个点，并且这两条路互相都没有交叉（也就是没有除起点终点外的相同的点）。那我们首先判断这两个点是否连通（这一步可以使用iscircle或者并查集）。第二步，找割点。通俗来说就是依次去掉路径上的点，这两个点还有没有连通。如果存在一个点，当去掉它时，两个点不连通了，说明这个点是路径必经的点（也就是不管有多少条路，都回到这个点）。说明点之间并不点双连通。那么如果不存在这样的点，那么点双连通。这里找割点的方法其实可以暴力一点，直接枚举其他的点，再删除他们，查看两点是否连通。要注意的是，并查集不支持删除点之后的查询，所以建议删除点之后用dfs或bfs检查连通性。这个方法思路较为简单也很好理解，但是缺点就在于他的时间复杂度比较高，大概是O(n^2)级别的。

　　第二个方法就是tarjan算法。这个算法我并不会具体阐述怎么实现，网上有很多讲得不错的资料。大致思路就是，我从一个点出发，一直走，发现了一个强连通分量（这里用有向图的概念，无向图也可以类比），就把所有涉及到这个强连通分量的点都记录下来。那么我们使用tarjan算法，就可以求到这个图的所有最大强连通分量。我们stronglinked函数需要的更加简单，就是每次找出一个极大强连通分量时，判断两点是否在其中，如果在，那么点双连通。如果不存在这样的强连通分量，那么点双连通就不存在。

 

五、bug分析和修复情况

 

　　本次作业我在第二次和第三次都发现了自己的bug。

　　第二次作业我栽的十分惨烈，原因是我在维护ageMean的时候，现将ageMean求出，等到再加一个人的时候就乘以人数，补充新增的age，再除以人数+1。这样sb的公式我居然没有半点怀疑他是错的，因为这里使用的都是取整，所以误差会因为一次次增加age而增大，导致最后ageMean不准确。我其实这次作业跟同学对过拍，可惜的是我们两个人犯了同样的错误，这也给我一个很大的教训。

　　这个bug的解决方式也很简单，直接增加一个agesum，每次需要ageMean的时候除以人数。

　　第三次作业的bug十分明显，但还好，测评数据没有给我挖坑，不然我的强测又无了。在判断stronglinked的时候，存在一种情况，如果求出来的强连通分量只存在起点和终点时，这种情况是不算stronglinked的，但是我算进去了。

这个bug的解决方式仍然十分简单，只需要多判断一个点数大于2即可。

 

六、心得体会

 

　　总的来说，这次作业难度不算大，因为规格写的非常详细，需要考虑的就是怎样完整而严谨的实现规格并进行合理地优化。但是我在第一点就做的不够好，测试不够到位导致我出现了这两个小bug，其中一个还让我直接没有进room。但是这个单元也让我学到了很多，尤其是在复习离散数学这方面，我觉得我又找回到了学离散数学的感觉。