隐马尔科夫模型HMM（一） -- 模型介绍

       目前在工作中使用到了jieba分词，主要是对文章进行切词，在深入理解jieba切词原理的时候，发现其采用了隐马尔科夫模型HMM，因此对HMM进行了研究，这里就自己学习到的知识进行记录。文章主要参考了宗成庆老师的《统计自然语言处理》第二版，非常感谢宗老师！

一、马尔科夫模型

       马尔可夫模型是一类随机过程。它的原始模型马尔可夫链，由俄国数学家A.A.马尔可夫于1907年提出。
       马尔科夫假设：随机过程中各个状态$O_t$ 的概率分布，只与它前一个状态$O_{t-1}$有关，即
$$P\left(O_t|O_1,O_2,O_3...O_{t-1}\right)=P\left(O_t|O_{t-1}\right)$$
       一阶马尔可夫链：符合马尔可夫假设的随机过程，即随机过程中各个状态$O_t$ 的概率分布，只与它前一个状态$O_{t-1}$有关。

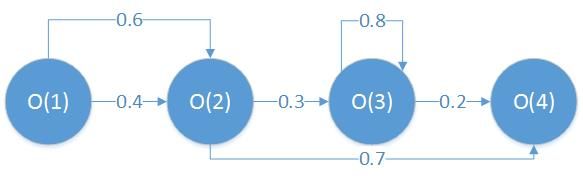
       马尔可夫模型形式化表述：
$$\mu =\left(S,\pi ,A\right)$$
S：所有可能的状态集合
$\pi$：初始状态概率
A：转移状态概率

二、隐马尔科夫模型HMM

1、HMM举例

       在马尔科夫模型中，每个状态代表了一个可观察的事件，所以马尔科夫模型又称为可视马尔科夫模型。在 隐马尔科夫模型HMM中，我们不知道模型所经历过的状态序列，只知道状态的概率函数，也就是观察到的事件是状态的随机函数。因此，HMM是一个双重的随机过程，其中模型的状态转换过程是隐藏的，可观察事件的随机过程是隐藏状态转换过程的随机函数。
       如下图所示为HMM的基本原理：

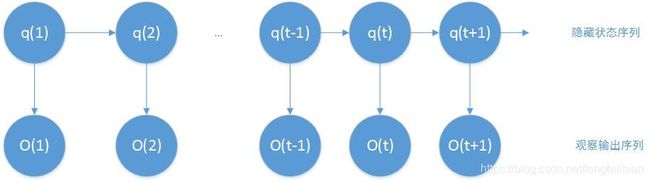
       下面举例对HMM的含义进行说明。假如一个暗室中有N个口袋，每个口袋中有M个不同颜色的球。一个实验员根据某一概率分布随机地选取一个初始口袋，从中根据不同颜色的球的概率分布，随机取出一个球，并向室外的人报告该球的颜色。然后，再根据口袋的概率分布选择另一个口袋，根据不同颜色的球的概率分布从中随机的选择另一个球，重复这个过程。对于室外的人来说，可观察到的只是不同颜色的球的序列，而口袋的序列是不可观察的。在这个过程中，每个口袋对应于HMM中的状态，球的颜色对应于HMM中状态的输出符号，从一个口袋转移到另一个口袋对应于状态转换，从口袋中取出球的颜色对应于从一个状态输出的观察符号。
       因此，一个HMM由以下几部分组成：
（1）模型中状态的数目N（口袋的个数）
（2）从每个状态可能输出的不同符合的数目 M（球的不同颜色的数目）
（3）状态转移概率矩阵$A=\left\{a_{ij}\right\}$（$a_{ij}$是实验员从一个口袋$s_i$转向另一个口袋$s_j$取球的概率），其中，
$$\begin{gathered} a_{ij}=P\left(q_t=s_j|q_{t-1}=s_i\right),1\le i,j⩽N \\ {a}_{ij}⩾0 \\ \sum _{j=1}^N{a}_{ij}=1 \end{gathered}$$
（4）从状态$s_j$观察到符号${\nu }_k$的概率分布矩阵$B=\left\{b_j\left(k\right)\right\}$（$b_j\left(k\right)$为实验员从第j个口袋中取出第k中颜色的球的概率），其中
$$\begin{gathered} b_j\left(k\right)=P\left(O_t={\upsilon }_k|q_t=s_j\right),1\le j⩽N;1\le k⩽M \\ {b}_j\left(k\right)⩾0 \\ \sum _{k=1}^M{b}_j\left(k\right)=1 \end{gathered}$$
观察符号的概率又称符号发射概率。
（5）初始状态概率分布$\pi =\left\{{\pi }_i\right\}$，其中
$$\begin{gathered} {\pi }_i=P\left(q_1=s_i\right),1\le i\le N \\ {\pi }_i\ge 0 \\ \sum _{i=1}^N{\pi }_i=1 \end{gathered}$$
       一般地，一个HMM记为一个五元组$\mu =\left(S,K,A,B,\pi \right)$，其中S为状态的集合，K为输出符号的集合，$\pi ,A,B$分别是初始状态的概率分布、状态转移概率和符号发射概率。

2、HMM的重要假设

（1）齐次马尔科夫假设：任一时刻 t 的状态只依赖于其前一时刻的状态，与其它时刻的状态及观测无关，也与时刻 t 无关。即
$$P\left(q_t|q_1,q_2,q_3...q_{t-1}\right)=P\left(q_t|q_{t-1}\right)$$
（2）观测独立性假设：任意时刻的观察状态只仅仅依赖于当前时刻的隐藏状态，与其它时刻的状态及观测无关。即
$$P\left(O_t|q_1,q_2,q_3...q_{t-1}{O}_1,O_2,O_3...O_{t-1}\right)=P\left(O_t|q_t\right)$$

3、HMM观察序列的生成

输入：HMM模型$\mu =\left(S,K,A,B,\pi \right)$，以及观察序列的长度T
输出：观察序列$O=O_1{O}_2{O}_3...O_T$
生成过程如下：
（1）根据初始状态的概率分布${\pi }_i$选择一个初始状态$q_1=s_i$;
（2）设t=1;
（3）根据状态$s_i$的输出概率分布$b_i\left(k\right)$输出$O_t={\nu }_k$；
（4）根据状态转移概率分布$a_{ij}$，将当前时刻t的状态转移到新的状态$q_{t+1}=s_j$；
（5）t=t+1，如果t

4、HMM中的三个基本问题

（1）估计问题：给定一个HMM模型$\mu =\left(S,K,A,B,\pi \right)$和观测序列$O=O_1{O}_2{O}_3...O_T$，如何快速地计算出给定模型$\mu$的情况下，观察序列O的概率，即$P\left(O|\mu \right)$？
（2）序列问题：给定一个HMM模型$\mu =\left(S,K,A,B,\pi \right)$和观测序列$O=O_1{O}_2{O}_3...O_T$，如何快速有效地选择在一定意义下“最优”的状态序列$Q=q_1{q}_2{q}_3...q_T$，使得该状态序列“最好的解释”观察序列，也即是$P\left(Q|\mu ,O\right)$最大？
（3）参数估计问题：给定一个观察序列$O=O_1{O}_2{O}_3...O_T$，如何根据最大似然估计来求模型的参数值？即如何调节模型$\mu =\left(S,K,A,B,\pi \right)$的参数，使得$P\left(O|\mu \right)$最大？