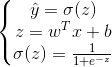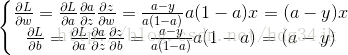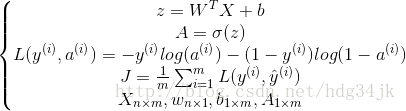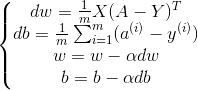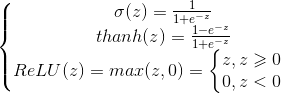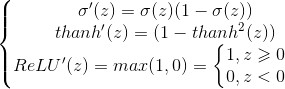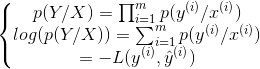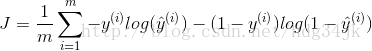吴恩达学习—Logistic Regression

吴恩达机器学习第一课便是Logistic Regression，这个算法是一种常见的分类算法，因其使用了logistic函数，由此得名。Logistic Regression可以看成0个隐层的神经网络，学通该算法，对研究神经网络有很大帮助。

1.正向传播
Logistic Regression 算法如下图所示，假设与y的相关的特征为x，通过输入特征x各分量的线性相加，再经非线性函数变换，就可以得到y的估计值，其中w与b是线性叠加中的参数。

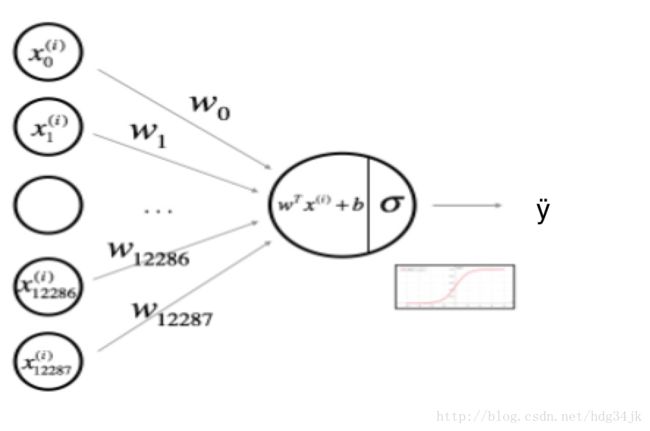
将以上过程写成如下公式：

其中σ是激活函数，稍候将会介绍三种常见的激活函数。

接下来将比较估计值与y之间的差距，这个差距通常叫做损失函数，然后最小化损失函数就可以达到训练模型的效果。通常损失函数有以下两种：

对于第一种损失函数，在Logistic Regression中并不常用，因为在优化参数时，优化问题通常会变成非凸问题，非凸问题会有多个极小点，导致陷入局部最优解。
第二种损失函数比较常用，下图解释了为何优化该损失函数达到训练模型的目的，文章最后将会介绍该损失函数的推导过程。

训练模型时通常会有多个样本，需要对所有样本的损失函数求平均，以代表训练集的损失，通常将这种损失称为成本函数：

2.反向传播
以上过程称为Logistic Regression 正向传播过程，下面将介绍如何利用梯度下降法反向传播。反向传播就是通过梯度下降最小化成本函数，首先求解梯度(中间过程略去)：

求出梯度后，就可以更新参数了：

其中α是学习步长

最后将正向反向过程向量化，利用矩阵计算加快计算速度。
正向传播过程：

反向传播过程：

不断迭代正向反向传播，就可以得到最优的训练参数。

3.常用激活函数：
三种常见激活函数及其导数如下：

目前神经网络中隐层多使用ReLU函数，因为对于z>0，它的梯度都是相同的，梯度不会随着z变大或变小而变小，从而导致收敛速度变慢。Python中可以这样实现ReLU函数np.maximum(z,0)，其导数为(z>0).

4.损失函数推导过程

对于二类分类问题，y只有0与两种取值，假设估计值是输入为x，输出为1的概率，则如下关系成立：

定义p(y/x)为如下形式：

为方便计算，两边取对数，则得到如下公式：

上面的负号是因为，我们希望概率越大越好，而损失函数越小越好，因此概率与损失函数差一个负号。对于多个样本而言的成本函数，可以使用最大释然估计求得：

除以m来控制成本函数的缩放，并加负号得到成本函数：

5.Pyton源码
用Python将以上过程实现，Python源码如下：

import numpy as np
import h5py
import matplotlib.pyplot as plt
import matplotlib
import scipy
from PIL import Image
from scipy import ndimage
from lr_utils import load_dataset
%matplotlib inline
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
m_train = np.shape(train_set_x_orig)[0]
m_test = np.shape(test_set_x_orig)[0]
num_px = np.shape(test_set_x_orig)[1]
train_set_x_flatten = train_set_x_orig.reshape(m_train, -1).T
test_set_x_flatten = test_set_x_orig.reshape(m_test,-1).T
n_train = np.shape(train_set_x_flatten)[0]
train_set_x = train_set_x_flatten / 255.
test_set_x = test_set_x_flatten / 255.
def sigmoid(z):
    s = 1/(1 + np.exp(-z))
    return s
def initialize_with_zeros(dim):
    w = np.zeros((dim, 1))
    b = 0
    assert(w.shape == (dim, 1))
    assert (isinstance(b, float) or isinstance(b, int))
    return w, b
def initialize_with_zeros(dim):
    w = np.zeros((dim, 1))
    b = 0
    assert(w.shape == (dim, 1))
    assert (isinstance(b, float) or isinstance(b, int))
    return w, b
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
    costs = []
    for i in range(num_iterations):
        grads, cost = propagate(w, b, X, Y)
        dw = grads["dw"]
        db = grads["db"]
        w = w - learning_rate * dw
        b = b - learning_rate * db
        if i % 100 == 0:
            costs.append(cost)
        if print_cost and i % 100 == 0:
            print ("cost after iteration %i: %f" %(i, cost))
    params = {"w":w,
             "b":b}
    grades = {"dw":dw,
             "db":db}
    return params, grads, costs
def predict(w, b, X):
    m = X.shape[1]
    y_prediction = np.zeros((1, m))
    w = w.reshape(X.shape[0], 1)
    z = np.dot(w.T, X) + b
    A = sigmoid(z)
    print "A shape" + str(A.shape)
    for i in range(m):
        if A[0, i] <= 0.5:
            y_prediction[0, i] = 0
        else:
            y_prediction[0, i] = 1
    assert(y_prediction.shape == (1, m))
    return y_prediction
def model(x_train, y_train, x_test, y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False):
    n = x_train.shape[0]
    print n
    w, b = initialize_with_zeros(n)
    params, grads, costs = optimize(w, b, x_train, y_train, num_iterations, learning_rate, print_cost)
    w = params["w"]
    b = params["b"]
    y_train_predict = predict(w, b, x_train)
    y_test_predict = predict(w, b, x_test)
    print "train accuracy:{} %".format(100 - np.mean(np.abs(y_train_predict - y_train)) * 100)
    print("test accuracy: {} %".format(100 - np.mean(np.abs(y_test_predict - y_test)) * 100))
    d = {"costs":costs,
         "y_train_predict":y_train_predict,
         "y_test_predict":y_test_predict,
         "w":w,
         "b":b,
         "num_iterations":num_iterations,
         "learning_rate":learning_rate}
    return d