CS229 笔记：关于 Logistic Regression 的六个小问题

*Andrew Ng.在斯坦福讲授的CS229是非常好的机器学习入门材料。我很后悔现在才开始学。个人认为这份材料的厉害之处在于，与一些普通的视频课程相比，CS229的视频与笔记互相补充，把一些关键问题讲得明明白白；与一些教科书相比，CS229的思路非常自然，让人觉得学完之后就能把这些知识搞清楚，而一般教科书罗列的知识点却让人越学越糊涂。
课程在2008年录过一次像，这是目前为止唯一版本的公开视频。全部笔记在课程官网上有，应该还是2012年版的。习题集是2016年的。

0. 引入

虽然叫做“Regression”，但 Logistic Regression 实际上是一种“Classification”算法。它的一些中文译名特别奇葩，本文采用周志华教授的“对率回归”，后面会解释原因。
很多机器学习的学习资料都把对率回归作为第一种分类算法来讲解，盖因其简单易懂，而且在工业界对率回归也是最常用的算法之一和机器学习、数据挖掘岗位的必考内容。所以这则笔记将围绕对率回归，试图把一部分有意思的问题理出些思路来。
本文内容主要参考了 CS229 Note、《统计机器学习》和《机器学习》（周志华）三份材料。

对率回归的假设非常简单：

hθ(x)=g(θTx)=11+e−θTx

g(z)=1/(1+e−z) 称为“对率函数”。 g(z) 的函数曲线：

1. 对率函数的中文翻译

目前为止，笔者见过的 logistic regression 的中文翻译主要是有逻辑斯蒂回归和逻辑回归两种，“回归”没有问题，主要在 logistic 怎么解释。
“逻辑斯蒂”显然是音译，为《统计机器学习》所采用。
第二种“逻辑回归”的“逻辑”在于， logistic regression 处理的是 {0, 1} 分类问题。
看似有理，其实不通。Logic 确实像 logistic 的词源，但在此处的语境下，后面提到的 logit 比 logic 更接近 logistic 的内涵； logistic 是取值范围在 （0, 1） 上的连续可导函数，而不是 0-1 二值； 0/1 loss 的设计是在用 logistic 函数去逼近 0/1 分类。
并且中文的“逻辑”有特定的意义，与 logistic 并不适配。

如果从词源来考虑，看起来像是复数形式的 logistics 有“后勤”“物流”的意思。据说 logistics 作“物流”解时，源头是希腊文 logistikos “计算的科学”。法国大革命时期，拿破仑的政史官A.H.若米尼在总结攻俄失败的报告中首先使用了 logistics 来指代军需物资的运输。

Logistic 曲线最早是比利时数学家皮埃尔·弗朗索瓦·韦吕勒（Pierre-François Verhulst（1804-1849））命名的，用来刻画比利时人口数据与物资供应量之间的关系（写到这里忽然想起来，中学生物里讲生态的一节，讲到刻画种群中个体数量与时间的关系时也有类似的“S形曲线”）。不过韦吕勒没有解释为什么这么取名。

《机器学习》和《统计机器学习》中都解释过“对率”的意义：
一个事件发生/样本 x 作为正例的概率，与其不发生/样本 x 作为反例的概率，两者的比值称为“几率”（odds），写作 odds=y/(1−y) ，反映了 x 作为正例的相对可能性。它的对数 logodds=logy/(1−y) ，也叫 logit。
把对率函数的表达式 y=1/(1+e−(wTx+b)) 带入 log odds，且让此处的 y 表示 p(y=1|x) ，那么就有了

logp(y=1|x)p(y=0|x)=wTx+b

可见，对率回归有点像是“在用线性回归模型的预测结果去逼近真实标记的对数几率”。这就是《机器学习》中“对数几率”的来由和内涵。
需要区分， logistic 并不是对数的（log）也不是对数线性 log-linear，而是 对数几率 logit。

2. 从广义线性模型到对率函数

从概率的观点考虑，线性回归问题中 y|x;θ ~ N(μ,σ2) ，对率回归问题中 y|x;θ ~ Bernoulli(ϕ) 。
可以证明，它们都是广义线性模型的特例。

广义线性模型有三个假设：

1. y|x;θ ~ ExponentialFamily(η) （以 η 为参数的指数族）.
2. 自然参数 η 与输入 x 之间是线性关系： η=θTx .
3. 需要预测的目标值 T(y) 。通常令 T(y)=y ，表示我们想要让假设 h 输出的预测 h(x) 满足 h(x)=E[y|x] .

指数族可以写成下面的形式

p(y;η)=b(y)exp(ηTT(y)−a(η))

η 自然参数（natural parameter）,
T(y) 充分统计（sufficient statistic），通常令 T(y)=y ,
a(η) 称为对数配分函数（log partition function）.

对于一个伯努利分布 B(ϕ) ，y取 {0,1} ，

p(y;ϕ)=ϕy(1−ϕ)1−y=exp(ylogϕ+(1−y)log(1−ϕ)=exp((log(ϕ1−ϕ))y+log(1−ϕ))

对照上方的指数族，令 η=log(ϕ/(1−ϕ)) ，伯努利分布就可以纳入指数族中。
而根据 η=log(ϕ/(1−ϕ)) ， 很自然地就得到了 ϕ=1/(1+e−η) ，恰好就是对率函数。即由广义线性模型可以推出对率函数的形式。

3. 对率回归与高斯判别分析

对率回归还与高斯判别分析（gaussian discriminant analysis，GDA）有相当的关联性。
GDA是一种生成模型（generative learning algorithm），不同于判别模型（如对率回归）从数据中学习 p(y|x) 以实现类别判断，生成模型学的是 p(x|y) ，即学习从类别中生成数据的特定分布。在对类别先验 p(y) 和 p(x|y) 建模后，根据贝叶斯准则可以得到后验分布

p(y|x)=p(x|y)p(y)p(x)

GDA 是一种比较简单的生成模型，它假定 p(x|y) 服从多元正态分布 N(μ,Σ) 。 μ 是均值向量， Σ 是协方差矩阵。
GDA 用于分类任务时，输入向量要求是连续随机变量。以二分类问题为例，模型为

yx|y=0x|y=1∼Bernoulli(ϕ)∼N(μ0,Σ)∼N(μ1,Σ)

写出概率分布

p(y)p(x|y=0)p(x|y=1)=ϕy(1−ϕ)1−y=1(2π)n/2|Σ|1/2exp(−12(x−μ0)TΣ−1(x−μ0))=1(2π)n/2|Σ|1/2exp(−12(x−μ1)TΣ−1(x−μ1))

利用最大似然估计求解这些参数，就能得到模型的解。

那么GDA 与对率回归有什么关系呢？
如果把 p(y=1|x;ϕ,μ0,μ1,Σ) 看作 x 的函数，带入贝叶斯公式，整理之后可以得到

p(y=1|x;ϕ,Σ,μ0,μ1)=11+exp(−θTx)

推导过程可参考CS229的 problem set 1.
假设 p(x|y) 是协方差矩阵相同的多元高斯，可以推出它的后验 p(y|x) 就是对率函数，但 反过来不成立，即 多元高斯是对率后验的充分非必要条件，所以多元高斯模型是比对率回归更强的假设。
这样一来，如果模型对于数据分布的高斯假设是正确的 (即 p(x|y)∼N(μ,Σ) )，那么 GDA 的结果会比对率回归更好（因为具备了更明确的先验）——事实上可能是最好的模型（废话）。
但反过来说， 由于对率回归的假设更弱，那么在 数据不符合多元高斯假设的情况下，对率回归的 robustness 更好、泛化能力也更强。
举例来说，当 x|y=0∼Poisson(λ0) 时 p(y|x) 也是对率的——其实，只要 x|y 的概率密度函数在指数族中，它的后验都是对率的。
证明请参考 CS229 的 lecture 5。

4. 为什么对率回归是个好模型

这个问题本身就做了一部分解释。
越简单的模型，假设就越宽松，对不能确定分布情况的数据的泛化性也就更好；模型简单，计算量就小，编程实现就简单。对率回归的流行源于它的实用性和适应性。因为这些良好的特性，对率回归经常作为部署新平台时的 baseline 算法。

而从模型本身来看，对率回归满足分类任务的需要（别忘了我们是来干什么的）：将 (−∞,+∞) 平滑映射到区间 [0,1] 上；它的导数计算简单—— g′(z)=g(z)(1−g(z)) ——这样使用梯度下降、牛顿法等一阶二阶优化工具求解起来就比较容易。

5. 对率函数与 sigmoid 函数的关系

以前查资料的时候还看到过一个问题。有人分不清对率函数和 sigmoid 函数，经常把二者搞混。
Logistic 对率函数毫无疑问就是上方图形中所呈现的样子。
严格按定义来看，Sigmoid 函数是一类状如“S”的曲线，但在一般使用中，人们经常用 sigmoid 去指代对数几率，这是不严谨的用法，但就像词语含义的演变，将错就错了。
实际上对数几率属于 sigmoid。而根据“S形”的定义，其他函数如 tanh 具有类似的形状，也应当属于 sigmoid 的范畴。

6. 对率回归与神经网络的关系

历史上，神经网络由感知器模型演变而来，感知机的表达式是

y=sign(θTx+b)

图形可以画成

将符号函数换为 sigmoid 函数、增加“ y ”的个数，所谓的两层神经网络就出现了。继续增加层数，就得到了我们最熟悉的神经网络模型。

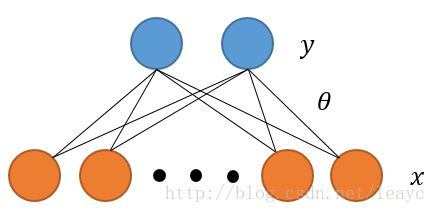
显然，如果不增加“y”只更换符号函数，感知机模型就变成了对率回归：

y=11+exp(−θTx+b).

结语

–update1–
由于精力有限外加才疏学浅，本文对上述问题只是稍有触及，并未做详细解释，还望见谅。有兴趣的朋友可以自己检索相关信息以备进一步讨论。
–update2–
最后一条的论述非常不严谨，以后会单写一遍 logistic 、softmax 和神经网络关系的笔记。

参考

1. CS229 Note 1, Stanford.
2. 周志华《机器学习》
3. 趣谈“logistic”：物流？后勤？还是“逻辑斯谛”？ https://mp.weixin.qq.com/s/wlCJNo3oqNOZ67-Vhx2Uhg
4. 李航《统计机器学习》
5. 周志华的新浪微博，关键词“logistic” https://weibo.com/zhouzh2012?topnav=1&wvr=6&topsug=1&is_all=1&is_search=1&key_word=logistic#_0
6. 广义线性模型的Wikipedia
7. https://www.quora.com/Is-there-any-difference-between-sigmoid-logistic-and-tanh-function