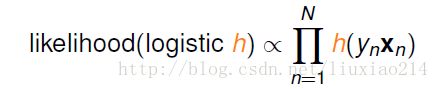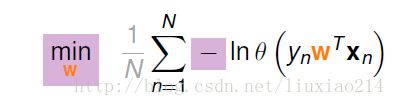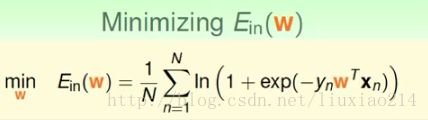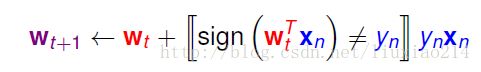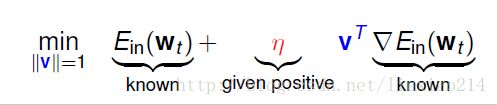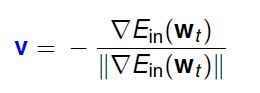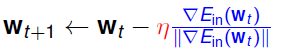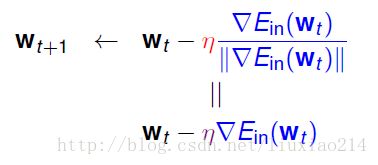【ML&DL】logistics regression理解

---

以前有学过linear classification、linear regression和logistics regression，这次做一下总结，并主要推导一下交叉熵损失函数的由来和梯度下降法。

---

一、概述

开头先祭出林轩田老师讲义中的一张图

PLA、Linear Regression到logistics regression的区别。

误差函数由0/1误差演变为均方误差到交叉熵误差。

1.1 PLA/Pocket

PLA是针对线性可分的数据，进行二分类，使用0/1误差，初始化权重，然后迭代更新，当有一个分类错误点时，就纠正权重，Wt+1=Wt+Yn(t)*Xn(t)，直到没有错误为止。

后来为了处理非线性可分数据，引入pocket，不再是找那个没有分类错误的权重，而是在迭代过程中记录每次权重放错的次数，经过足够多的权重后，去犯错最后的那个权重作为结果。

1.2 Linear regression

linear regression主要可以用来解决预测银行卡额度问题、预测房价问题等。使用均方误差。

暂时先不做过多说明。

直接进入logistics regression。

二、logistics regression

2.1 基本介绍

当我们在做预测心脏病是否复发的问题时，我们不可能给出一个是或否的回答，只能说，有多少的概率会复发。但是，我们的训练数据只有复发或不复发两种，而我们希望拿到的训练数据是有概率的。

这样就引入了logistics 函数，通过一个映射，将其转换为0-1之间的数，用来表示概率。

logistics 函数： f(x)=11+e−x f ( x ) = 1 1 + e − x

于是，得到假设函数：

那我们如何来优化这个假设函数呢，使用什么样的误差函数呢？这里就引入了交叉熵损失函数。

2.2 推导交叉熵损失函数

假设我们有这样一堆数据，

我们的目标函数产生这个数据集的概率为:

P(D)=p(x1O)p(x2X)p...p(xNX) P ( D ) = p ( x 1 O ) p ( x 2 X ) p . . . p ( x N X )

公式中，大写O为正分类O，大写X为负分类X

由于我们知道，已知数据 x1 x 1 ，产生O 的可能性就是我们的目标函数f(x)，索所以可得：

由条件概率的公式可得：

P(B|A)=P(AB)P(A) P ( B | A ) = P ( A B ) P ( A )

所以，产生数据集D的概率公式可表示为：

P(D)=p(x1)f(x1)∗p(x2)(1−f(x2))∗...∗p(xN)(1−f(xN)) P ( D ) = p ( x 1 ) f ( x 1 ) ∗ p ( x 2 ) ( 1 − f ( x 2 ) ) ∗ . . . ∗ p ( x N ) ( 1 − f ( x N ) )

但我们并不知道目标函数f，我们只能通过假设函数h，让其去逼近f，这样，我们可以推测，假设函数h产生数据集D的概率与目标函数f产生数据集D的概率逼近。

于是得到：

P(D)=p(x1)h(x1)∗p(x2)(1−h(x2))∗...∗p(xN)(1−h(xN)) P ( D ) = p ( x 1 ) h ( x 1 ) ∗ p ( x 2 ) ( 1 − h ( x 2 ) ) ∗ . . . ∗ p ( x N ) ( 1 − h ( x N ) )

由于logistics函数的特性， 1−h(x)=h(−x) 1 − h ( x ) = h ( − x ) ，则

P(D)=p(x1)h(x1)∗p(x2)h(−x2)∗...∗p(xN)h(−xN) P ( D ) = p ( x 1 ) h ( x 1 ) ∗ p ( x 2 ) h ( − x 2 ) ∗ . . . ∗ p ( x N ) h ( − x N )

由于p(x)这一项对我们的概率没有影响，可以去掉，变为：

P(D)=h(x1)∗h(−x2)∗...∗h(−xN) P ( D ) = h ( x 1 ) ∗ h ( − x 2 ) ∗ . . . ∗ h ( − x N )

将里面的正负号去掉，可以添加 yn y n ，代表二分类的0/1。

于是变为：

P(D)=∏Nn=0h(ynxn) P ( D ) = ∏ n = 0 N h ( y n x n )

我们求最优的假设函数时，即是从假设空间H中选一个产生D概率最高的函数，在数学上，称之为似然，即求最大似然。

于是，我们的目标现在变为：

而由于我们现在在做logistics，是求一个权值W，可以将W替代上图中的h，将有关W的式子带入：

于是得到：

但是这个式子我们不好处理连乘，于是加一个去对数，于是变为：

于是，将ln放进去后，连乘就变成了连加。于是变为:

maxw m a x w ∑Nn=0lnθ(ynwTxn) ∑ n = 0 N l n θ ( y n w T x n )

但是我们不想求max，求min比较容易，可以添加一个负号，并添加1/N，比较容易好计算，于是变为：

又由于 θ(s)=11+e−s θ ( s ) = 1 1 + e − s ,

所以上式可以化简为：

最终，得到交叉熵损失函数：

这就是交叉熵损失函数的由来。

2.3 优化方法：GD/SGD

有了损失函数后，我们就要对这个损失函数进行优化，尽可能降低这个损失，这里就是用到了经典的优化方法：梯度下降法。

我们得到损失函数后，

我们发现这个损失函数是连续可微凸函数，则只需找使梯度为0的权值w就可。即

Ein很容易求导，只需要运用链式求导法则即可，得到梯度为：

这样只要求解梯度为0的时候就可以。

我们可以看出，在梯度公式中， θ θ 函数如果全部为0，则梯度会等于0，所以知道，当 −ynw′xn − y n w ′ x n 趋向于负无穷大时，其 θ(−ynw′xn) θ ( − y n w ′ x n ) 会等于0，这就意味着， ynw′xn y n w ′ x n 要趋向于正无穷，这意味着所有的 yn y n 与 w′xn w ′ x n 同号，即数据集D线性可分，才会发生这种情况。

但如果不是线性可分呢，这种方法求梯度等于0就不可行。

这个梯度不是一个线性的方程式，直接求解梯度等于0会比较困难。

那这怎么办？

我们想到以前用过得PLA，

每次碰到错误分类时，就修正W，即

可以改成下面这种形式：

如果是一项错误项，w需要修正，取符号那里为1，可以进行修正，如果是正确的，取符号那里为0，不必进行修正，这样就可以把两种情况统一，即迭代时随机取一个样本进行更新。

进一步地，我们可以把这个公式总结为：

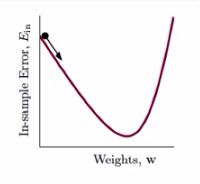
在更新时，一个是更新的方向，另一个是更新时要走多大一步。如下图：

进而地，我们可以用这种方法来得到logistics regression中的梯度为0的权重。

每次迭代时，选取合适的步长，合适的方向，这样得到最后想要的w，这种方法就是梯度下降法。

在PLA中，方向是我们错误修正的方向，步长是1。

那在logistics regression中，如何选择步长和方向呢？

那对于这种平滑的损失函数，我们可以怎么做呢？我们知道Ein长得就像一个山谷的形状，只要找到谷底的地方，就可以。直观上理解，就是迈着合适的步子，沿着最快到达谷底的方向。

为了推导出我们的v和 η η ，我们使用控制变量法。

首先推导v（滚下去的方向），则假设v的长度||v||=1，将走的长度都放到 η η 中去。

那我怎么找到这个最好的方向呢，假设我很贪心，当然是沿着最陡的方向往下走。即在方圆 η η 的空间中，我们沿着最陡的方向走。

但找这个最陡方向仍然很困难，容易做的是求解线性的问题。所以，我们将这个式子改为对于变量v是线性的。

对于弯弯曲曲的曲线，我们只看一小段的话，那他跟线段是一样的。就可以表示出一个线性关系。这里用到的思想就是泰勒展开式。那么上式就变成（如果 η η 够小的话）：

此时，我们的问题变为一个近似线性的问题。

在这个式子中，只有v是未知的。我们可以把多余的内容忽略掉， Ein(wt) E i n ( w t ) 是一个常数， η η 是我们给定的一个正数。所以我们只关注一下实体字的部分即可。找到一个v向量，能使得这个两个向量相乘的式子越小越好。

那两个向量相乘怎么样越小呢？就是两个向量方向相反，其内积就会最小。所以说向量v的方向就是梯度的反方向，但我们要求v是一个单位向量，所以v为：

这样就得到我们那个式子的最优解了。这就是我们想要的最好的v。

此时，我们的更新式子变为：

就是沿着梯度的反方向移一小步。

那我们现在再来推导 η η ，什么样的 η η 最好。

那什么样的 η η 不好呢？一种是每次走一小步，走了好久。另一种是走大步一点呢，那刚才我们用泰勒展开式，用线段来代替一小段的曲线就不准了，就好比，你以为你走了一大步，可以到达谷底，其实你跨到了另一个坡上，说不定到对面坡上没有下降，反而爬的更高。仍然没有下山。这种情况就没法确定。

那什么是好的步长呢？当然是适中的一步。就是说，当我的梯度比较大时，我可以跨大步一点，当梯度比较小时，可以跨小一点，

所以说 η η 是在变化的，随着梯度的大小变化的。即他们是正相关的关系。那如果 η||Ein(wt)|| η | | E i n ( w t ) | | 是成比例的关系，我们可以用新的 η η 来表示更新的式子，即：

所以，我们现在得到优化方法：

综上，优化方法介绍完毕。

2.4 logistics regression步骤总结

就这下图这么个过程。计算中最主要就是计算梯度。

---

后续：

1、GD就是在更新参数的时候，每次都是用全部的样本来进行计算。

优点是得到全局最优解，易于并行实现，缺点是当样本数多的时候，训练速度会很慢。

2、于是提出SGD，随机梯度下降法，每次随机是用一个样本来更新，更新多次。

优点是训练速度快，缺点是准确率下降，容易陷入局部最优解，不易于并行实现。

3、mini-batch GD：每次更新选择一部分样本，前两者的结合。

当然，后来又衍生了更多了优化方法，如Momentum、Nesterov、Adagrad、Adadelta、RMSprop、Adam、Adamax、NAdam。

具体可看博客：https://zhuanlan.zhihu.com/p/22252270，讲解的非常清楚。