OO第一单元总结——表达式求导
第一次作业
第一次作业较为简单,即对幂函数进行求导即可,也不需要判断表达式的合法性。需要注意的点为数可能很大,需要转换为BigInteger,其次常数要输出0。然后就用面向过程的思维写了大正则,一Main到底,然后使用HashMap便于化简。
**(1)基于度量来分析自己的程序结构 **
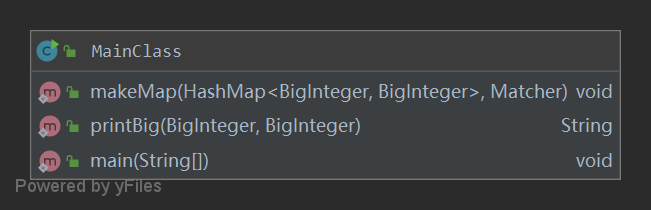
类很少,方法都在MainClass里面调用。
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| c.MainClass.main(String[]) | 3 | 6 | 6 |
| c.MainClass.makeMap(HashMap |
5 | 8 | 11 |
| c.MainClass.printBig(BigInteger,BigInteger) | 8 | 7 | 14 |
| Class | OCavg | WMC | |
| c.MainClass | 9 | 27 |
由上表,可看出在处理字符串和输出字符串的方法的基本复杂度很高,代码不易于维护和理解,圈复杂度较高,代码难于测试和维护。
唯一的优点就是比较短。
**(2)分析自己程序的bug **
公测前发现当求导为0时未输出,互测未发现bug。bug原因在于HashMap容器不包含元素,因为value为0的被remove,所以没有输出。
**(3)分析自己发现别人程序bug所采用的策略 **
写了一个python程序来生成测试用例,但没有写对拍程序,在找bug时就用生成的数据输入,找bug,发现两个人的bug,还有一人未发现。虽然这种方法属于广撒网,但其实不好捞鱼。因为生成的数据并不能涵盖所有情况,有的同学就x+x算错,你可能就生成不出来。
第二次作业
第二次作业中增加了三角函数,而且需要判断输入表达式是否合法,但不会因为空白字符而WORNG FORMAT!因为三角函数的内容较为简单,所以在第一次作业的基础上创建了一个类记录每一项幂函数、三角函数的指数。
**(1)基于度量来分析自己的程序结构 **
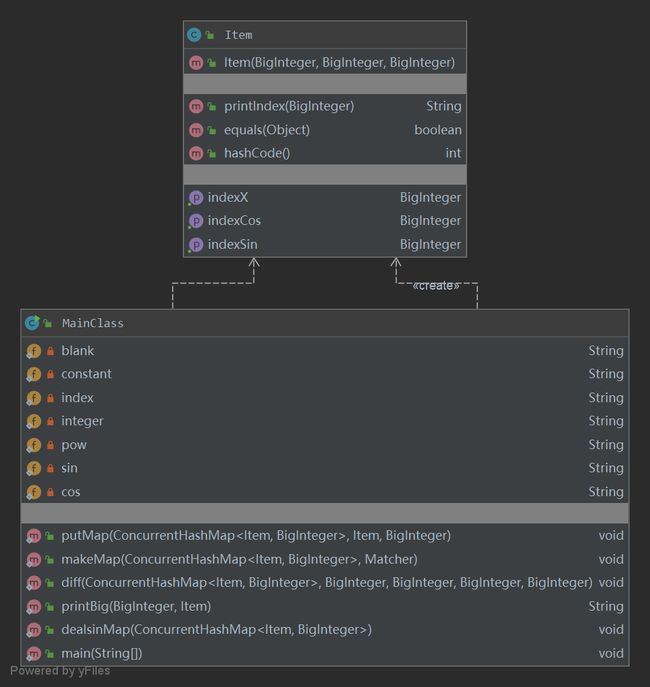
新建一个类Item记录每一项的幂函数和三角函数的指数,并作为ConcurrentHashMap的key值,来合并化简表达式。
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| c.Item.Item(BigInteger,BigInteger,BigInteger) | 1 | 1 | 1 |
| c.Item.equals(Object) | 3 | 4 | 6 |
| c.Item.getIndexCos() | 1 | 1 | 1 |
| c.Item.getIndexSin() | 1 | 1 | 1 |
| c.Item.getIndexX() | 1 | 1 | 1 |
| c.Item.hashCode() | 1 | 1 | 1 |
| c.Item.printIndex(BigInteger) | 3 | 11 | 16 |
| c.MainClass.dealsinMap(ConcurrentHashMap |
1 | 7 | 7 |
| c.MainClass.diff(ConcurrentHashMap |
3 | 3 | 5 |
| c.MainClass.main(String[]) | 4 | 8 | 8 |
| c.MainClass.makeMap(ConcurrentHashMap |
1 | 15 | 16 |
| c.MainClass.printBig(BigInteger,Item) | 1 | 1 | 1 |
| c.MainClass.putMap(ConcurrentHashMap |
4 | 3 | 4 |
| Class | OCavg | WMC | |
| c.Item | 3.14 | 22 | |
| c.MainClass | 6.33 | 38 |
由上表,可见第二次作业较第一次作业基本复杂度有降低,但部分方法模块设计复杂度变得很高,因为被其他模块多次调用,耦合度变得较高。
**(2)分析自己程序的bug **
在互测时被发现了bug,原因是在MainClass.dealsinMap中化简时忽略了HashMap不是多线程,在遍历key值时,同时移除了某些key,所以抛出了异常。所以后来上网查了一下,ConcurrentHashMap支持多线程,HashMap不支持。
**(3)分析自己发现别人程序bug所采用的策略 **
写了一个python程序来生成测试用例,但没有写对拍程序,在找bug时就用生成的数据输入,找bug,发现了一个人的bug,但是是WORNG FORMAT,所以无法hack,还有一个人在指数边界出错。互测应该是让我们看同学的代码来找bug,感觉丧失了意义。
第三次作业
第三次作业难度陡升,三角函数允许嵌套因子,还有表达式因子,所以无法写出一个大正则来匹配,所以重构了。使用递归的方法来求导。
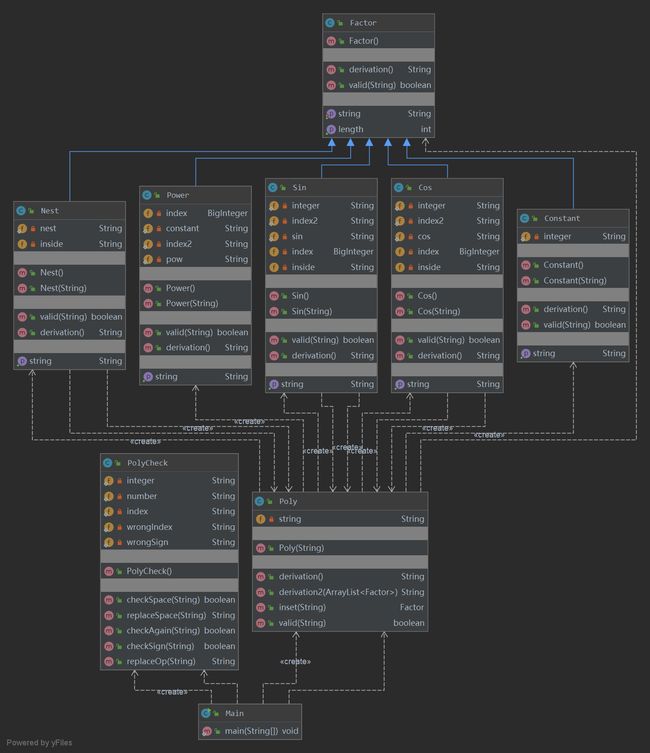
PolyCheck检查表达式的合法性,主要包括空白符,+-号;给每一种因子建立一种类继承自Factor;Poly就处理分割表达式。没有化简。
| Method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| Constant.Constant() | 1 | 1 | 1 |
| Constant.Constant(String) | 1 | 1 | 1 |
| Constant.derivation() | 1 | 1 | 1 |
| Constant.getString() | 1 | 1 | 1 |
| Constant.valid(String) | 2 | 1 | 2 |
| Cos.Cos() | 1 | 1 | 1 |
| Cos.Cos(String) | 1 | 4 | 4 |
| Cos.derivation() | 3 | 5 | 7 |
| Cos.getString() | 1 | 1 | 1 |
| Cos.valid(String) | 2 | 1 | 2 |
| Factor.Factor() | 1 | 1 | 1 |
| Factor.derivation() | 1 | 1 | 1 |
| Factor.getLength() | 1 | 1 | 1 |
| Factor.getString() | 1 | 1 | 1 |
| Factor.setString(String) | 1 | 1 | 1 |
| Factor.valid(String) | 1 | 1 | 1 |
| Main.main(String[]) | 1 | 7 | 7 |
| Nest.Nest() | 1 | 1 | 1 |
| Nest.Nest(String) | 1 | 3 | 3 |
| Nest.derivation() | 1 | 1 | 1 |
| Nest.getString() | 1 | 1 | 1 |
| Nest.valid(String) | 2 | 1 | 2 |
| Poly.Poly(String) | 1 | 1 | 1 |
| Poly.derivation() | 1 | 12 | 16 |
| Poly.derivation2(ArrayList ) | 1 | 4 | 5 |
| Poly.inset(String) | 6 | 1 | 6 |
| Poly.valid(String) | 6 | 1 | 6 |
| PolyCheck.PolyCheck() | 1 | 1 | 1 |
| PolyCheck.checkAgain(String) | 5 | 3 | 5 |
| PolyCheck.checkSign(String) | 2 | 1 | 2 |
| PolyCheck.checkSpace(String) | 8 | 2 | 8 |
| PolyCheck.replaceOp(String) | 1 | 1 | 1 |
| PolyCheck.replaceSpace(String) | 1 | 1 | 1 |
| Power.Power() | 1 | 1 | 1 |
| Power.Power(String) | 1 | 3 | 3 |
| Power.derivation() | 3 | 4 | 7 |
| Power.getString() | 1 | 1 | 1 |
| Power.valid(String) | 2 | 1 | 2 |
| Sin.Sin() | 1 | 1 | 1 |
| Sin.Sin(String) | 1 | 4 | 4 |
| Sin.derivation() | 3 | 5 | 7 |
| Sin.getString() | 1 | 1 | 1 |
| Sin.valid(String) | 2 | 1 | 2 |
| Class | OCavg | WMC | |
| Constant | 1.2 | 6 | |
| Cos | 2.8 | 14 | |
| Factor | 1 | 6 | |
| Main | 5 | 5 | |
| Nest | 1.4 | 7 | |
| Poly | 5.4 | 27 | |
| PolyCheck | 3 | 18 | |
| Power | 2.6 | 13 | |
| Sin | 2.8 | 14 |
第三次作业的平均基本复杂度、模块设计复杂度、圈复杂度较第二次作业都有降低。但是Poly.derivaton的复杂度较其他方法高,因为一直在循环调用其他方法。
**(2)分析自己程序的bug **
在强测和互测时被测出了bug,在Poly.derivation2(ArrayList )中,原因是给每一项求导时忽视了项前的符号,一直用+号连接。忽略这个bug是由于前两次作业一直使用HashMap保存系数,所以不需要考虑项之间的符号连接。但在第三次作业中,项与项之间通过+-号连接,这也是分割表达式的依据,传给Poly.derivation2(ArrayList )的也只是因子,忘记前面的+-号。后来更正的时候,Poly.derivation2(ArrayList )返回字符串时外面加一个括号也可以有效避免这个问题。
**(3)分析自己发现别人程序bug所采用的策略 **
写了一个python程序来生成测试用例,和对拍程序。但是,对拍写得不太对,只能区分特别明显的错误。发现了一个人的bug,但是还有其他人的bug未发现。因为这次表达式的复杂性,若只生成数据,肉眼是很难发现错误的。我觉得在互测方面,我还是得下点功夫。
应用对象创建模式
第一次作业主要是面向过程编程,可以将每一项创建一个对象,在对其求导。第二次作业在第一次作业的基础上添加了Item类,记录每一项的幂函数和三角函数的指数。第三次作业重构了,对每一种因子都创建了一个类,并继承自Factor类;PolyCheck检查表达式的合法性,主要包括空白符,+-号;Poly就分割表达式求导。
每一单元的作业的难度会逐渐提升,所以在第一次作业时就应该想好怎么创建对象,留一些余地扩展,以免给后面的作业增添太多压力,这样也比较符合实际。
对比和心得体会
对比优秀设计代码,我的设计明显还不够面向对象,也不够简洁。虽然我在前两次作业时较为轻松,但在第三次作业时几乎相当于重写了,若是第一次就想好了,之后也不会这么痛苦。
所以面向对象是关键,在对象改变时,添加几个类几个方法即可,不需要怎么改变结构,但面向过程即是,对象一旦改变,过程完全改变。
而且由于“一个人”设计代码,总会有遗漏的方面,而且常常难以发现,所以怎么构造测试样例也是一个关键。
希望在下次作业中,能考虑全面,而且能面向对象设计代码。