BUAA-OO-第一单元作业总结（表达式求导）

BUAA-OO-第一单元作业总结（表达式求导）

一、基于度量对程序的分析以及对象创建模式概况

1.第一次作业

        第一次作业在思路上并不是非常困难，由于没有格式检查的需要，并且因子形式只有幂函数形式一种，实现起来难度不大，项的切分也比较轻松，但是想要构建合适的类并不是一件容易的事，如果不能够充分分解，对于以后的迭代作业是及其困难的，下面是我在此次作业中的UML类图。

                                                                                                                       

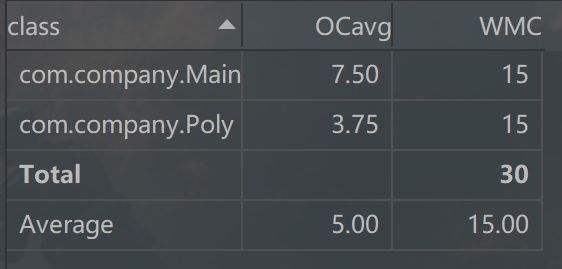
        这一次的作业，实话来讲我的对象结构构造并不是很好，还有很多面向过程的思想在里面，我只是简单地构造了一个Poly类，包含系数和指数，用来进行求导操作以及合并同类项来进行化简，此外还可以进行项的输出，返回一个字符串，剩下的操作，比如存储（使用了TreeMap)，正则表达式的分析，以及调整读入字符串的内容等等都放在了Main里，导致类的功能过于复杂，而且不利于后续的迭代开发，下面是此次作业的复杂度分析。  

                                                                                                                                                                                                                                                                                    

        可以看出，此次作业的复杂度主要集中在Main类中的main方法中，以及Poly类中的print方法中（应该是由于化简输出导致，情况较多，导致复杂度提升），因此平均复杂度比较高，而且仅有的两个类的耦合程度也非常高，这对于增量开发来讲就是灾难，在设计上没有仔细考虑将已有的类进一步细化，将不同的任务强行挤在了一起，对于第二次作业，基本不可能再次延续第一次作业的开发。

2.第二次作业

        第二次作业，不出意外地，我直接重构了，这一次作业算是体会到了一点面向对象构造与设计的意味了，这一次的内容是在第一次作业的基础之上，引入了新的因子sin(x)和cos(x)，并且需要进行格式检查来判断输入的表达式是否合法，难度相较于第一次有了一些提升，虽然进行了重构设计，但是整体设计还是比较流畅的，下面是本次作业的UML类图。

                                                     

        对于这一次的设计，首先，由于项的复杂化，不能够简单地继承第一次作业的做法，因此，我实现了一个Factor类的接口，包含一个求导的方法，然后，分别实现常数因子（ConstantFactor),  幂函数因子（XFactor) 以及三角函数因子（SinFactor和CosFactor)，都实现了求导方法，克隆方法，合并方法，均包含相应的系数和指数，然后，构建一个Item类，将得到的项依据*符号分割成不同的因子，并保存下来不同类型因子的指数以及常数因子的合并结果，其实这里比较适合工厂模式的应用，但是我觉得此次作业复杂度不高（没有嵌套）就没有实现这一模式，Item类里实现了克隆方法以及输出方法。

        对于格式检查，本次新建了一个Check类，用以实现正则表达式的合法判断，在按照形式化表述的规定实现了正则表达式的构造后，利用matcher()方法，先判断整体符不符合正则表达式，如果符合，再看循环判断指数是否合法，判断合法后，再将字符串处理，比如去掉括号，将多个连续的加减号化简，以及在字符串前面填补运算符，这样便于项的切分以及因子的切分，对于存储问题，本次作业实现了一个三元组KeyClass类，用来记录各个项的三种变量因子的指数，并且实现了equals方法以及hashCode方法，作为HashMap的key存储，方便合并同类项。

        对于三角函数的化简，讨论区里有人说可以利用递归的思想来求解，我没能理解，于是就实现了一个循环，来找哪两个项符合sin(x)**2+cos(x)**2，从而缩短输出的长度，在老师第四讲的总结中，我才意识到还有其他的公式可以用于化简，但是我没有考虑到，所以化简并不完全。

        下面是本次作业的复杂度分析：

                                                                                                           

                                                                                                          

        由于此次作业方法数太多，在此仅展示部分方法的复杂度分析，可以看到，相比于上一次作业，平均复杂度降低了一些，这充分说明了此次作业设计上还是可以接受的，主要的复杂点集中在了存储上，对于存储问题还是构思不足，我甚至需要用两个类来接力实现项的存储（Save类和Store类）这肯定是非常糟糕的设计，此外，求导类（Darivation类）复杂度也很高，这个类用于给项求导，具体思路就是Deri[f(x)*h(x)*g(x)] = Deri[f(x)]*h(x)*g(x)+f(x)*Deri[h(x)]*g(x)+f(x)*h(x)*Deri[g(x)]，并且只有一个方法，必然导致这个方法比较复杂，而且这种求导方式一旦遭遇了嵌套就要凉凉，还是需要改进。

3.第三次作业

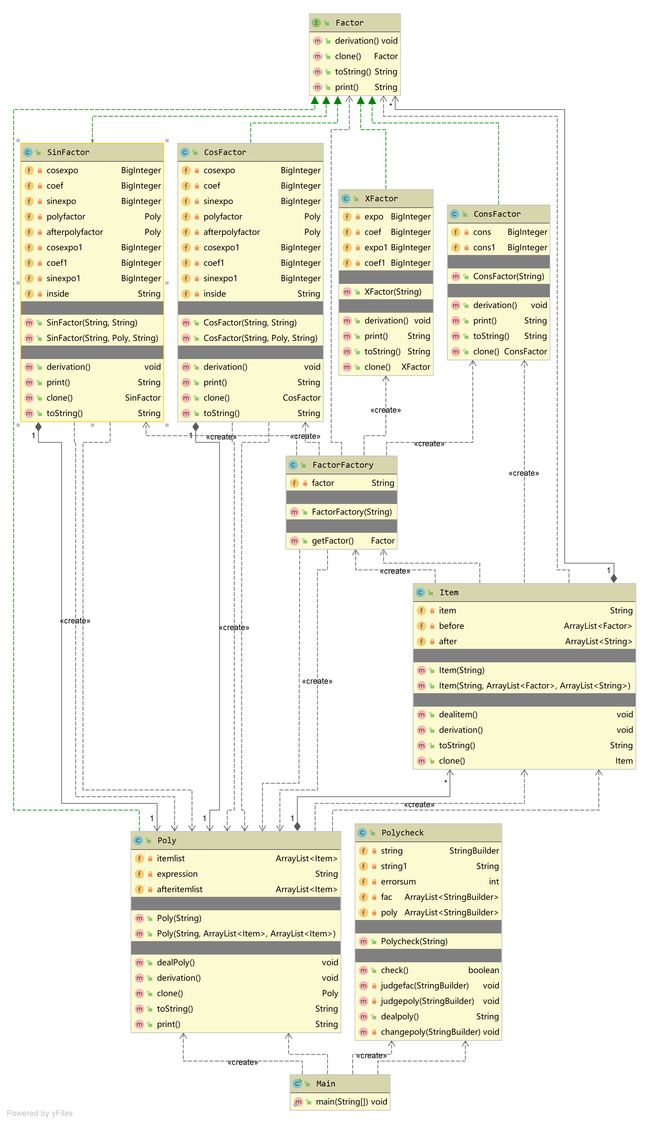
        这一次作业相较于上一次的难点，就在于嵌套的处理上，由于Java不支持递归定义正则表达式不论是求导还是格式检查都要进行修改，因此在一定程度上来讲，虽然我继承了第二次作业的一些已有代码，但还是重构了不少，下面是本次的UML类图。

                                                           

        首先说一下格式检查，收讨论区大佬们提出的递归思想以及缓存式存储的启发，虽然我没有实现递归的方法，但是，在判断玩有无不合法字符以及指数大小过后，我设立了两个ArrayList来存储因子和表达式，然后对于字符串中的表达式进行替换，将（）中的内容替换为#，将其存入表达式ArrayList中，sin()和cos()中的内容替换为@，将内容存入到因子ArrayList中，并且实现了判断因子和表达式是否合法的两种方法，然后利用while不停的循环，用同样的方法处理两个ArrayList中存储的内容，将产生的新的替换存入相应的容器中，指导没有新的内容需要处理为止，统计错误次数，并像第二次作业那样处理了字符串。

        对于字符串的处理，首先是实现一个多项式类（Poly类），并且要将其作为一种因子继承Factor接口，利用加减号来判断将多项式分解成项，再利用乘号将多项式分解成因子，本次作业我实现了一个工厂类，依据每种不同因子的特点（比如以何种字符串开头），生成不同种类的因子，由于包含嵌套的处理，本次作业为两个三角函数类增加了大量的属性用来适应嵌套操作，实现的不是很漂亮，有很多重复内容（虽然是用来做不同的工作的），而且细节处理不到位，导致强测爆了连个点。

        本次由于化简过难，且我的架构设计不是非常顺利（状态糟糕，连着两天什么都写不出来，差点心态爆炸），我就没有做任何化简工作，希望可以阅读其他人的优秀代码来弥补自己的遗憾吧。

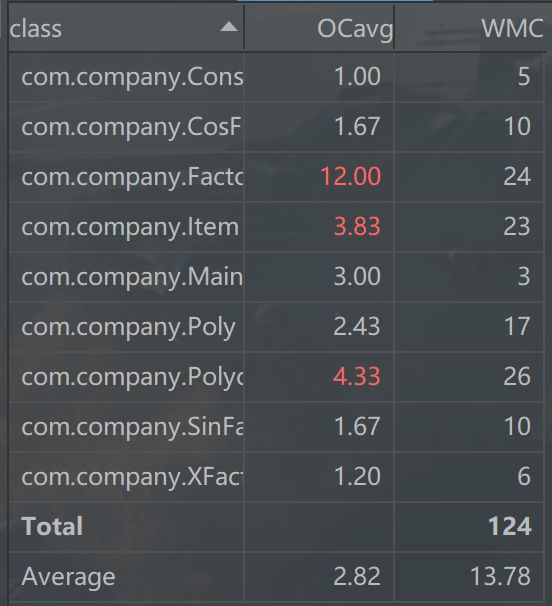
        下面是本次作业的复杂度分析：

                                                                                                        

                                                                                                    

        平心而论，如果设计得好，本次作业复杂度甚至可以比上一次要低，但是从数据来看，我的复杂度不降反升，一方面是由于嵌套带来的复杂性，另一方面就是我在类的实现过程中还是非常冗余，以工厂类来看，我的工厂类仅由一个方法组成，其中包含了分析与判断，极其冗长，且不易理解（由于没能够事先处理好字符串，导致我只能工厂类中处理），这个类就承担了不该它做的事，因此，我的代码还是需要打磨的。

二、bug分析以及hack策略

1.第一次作业

        第一次作业由于难度不高，我的强测以及互测都十分稳健地通过了，应该说没什么大的问题。

        在互测当中，由于我没有实现python自动化生成数据测评，所以我只能够自己构造数据测试，hack策略就是单纯的组合，不同的系数，指数，以及加减符号，特殊情况的考虑（比如1，-1,0这些数的处理，以及前导0），但是我没能够hack到其他人。

2.第二次作业

        这一次作业强测还是AC了，但是互测的时候我被集火打成了筛子。

        问题就在于项的求导上（Derivation类)，在对BigInteger类运算的时候，我没将运算得到的新值赋给原来的变量，导致我的求导过程中，系数其实没有发生变化（强测竟然测不出来），此外就是我的优化出了问题（不优化就没有bug是真理啊。。。），在三角函数合并的时候，比如2*sin(x)**2-3*cos(x)**2，会计算出错误的系数，导致错误。

        由于依旧没有自动化测评手段，我还是采用了组合的方式，增加了三角函数的考虑，以及针对三角函数优化的设计样例，但是可能除我以外大家的代码都很出色，我还是没能hack出来。

3.第三次作业

        这一次由于整个思路不是非常清晰，并且心态不好，导致本次作业完成的质量有所下降，连强测都没能全部通过（爆了2个），在互测的时候更是又被打成了筛子，原因是在工厂类当中以及多项式类当中，由于我没有充分考虑到多项式的格式特征（新分离出的多项式因子需要添加符号），导致我很多互测的点，比如sin((x+x**2+cos(x**2)))，都不能够正确运行，改正之后还存在了输出格式错误的现象，这就是多项式的输出问题又一次没有考虑好，导致这一次结果非常不如人意。

       这一次的构造样例，由于我在互测期间发现了自己的bug，于是我就主要针对自己的bug构造了样例，同时引用了灌水群里的一些大家提供的一些样例，这一次反倒hack到了3次，还是给我找补回来一点分数。

      细想一下，发现反倒是最不面向对象的第一次作业没有出现bug，而后两次出现了bug，真是讽刺，其实，只要我再仔细测试一下，完全可以发现问题所在，只不过要么自负了一下，要么烦躁了一下，就导致了不必要的失分，这是以后需要注意的。

三、对比和心得体会

        对比其他人的代码，我发现有很多人在第一次作业就在积极探索面向对象的方法，而不是像我一样待在舒适区里不愿出来，非得要无法解决问题的时候才能走出来，落得个次次重构的下场，我发现很多人真的是做到了比较完美的优化以及按照了指导书中的建议架构进行程序的编写，而我就都没能够做到（不知如何优化以及没能理解指导书中的想法），我是主要参考了网上以往同学的博客，参考了他们的思想（起码对我来说更好理解一些），我还是应该更细致地阅读指导书，更全面地思考一下我需要那些类，好好做做架构，俗话讲：磨刀不误砍柴工，有了优秀的架构，代码编写起来也会很快，只不过由于时间因素，我可能没办法全面设计出最让我满意的架构，这方面我只能够争取做到平衡吧。

        总而言之，第一单元的作业求导看似简单，实则暗藏玄机，极其适合使用工厂模式，做好了就可以体会到什么叫做迭代开发，感受到其中的奥妙而不是痛苦（再次强调架构的重要性），这三次作业下来，还是有不少遗憾，再努力一下下就可以做到更好，不管怎么说，也只能够整理心情再出发了，以后的单元不会更加容易，希望自己能够渡过难关，获取真知吧。

        最后贴一下工厂类的设计方法吧，希望大佬批评指正：

public Factor getFactor() {
    if (factor.startsWith("sin(")) {...} //SinFactor

    else if (factor.startsWith("cos(")) {...} //CosFactor

    else if (factor.startsWith("x")) {...}  //XFactor

    else if (factor.startsWith("(")) {...} //Poly

    else {...} //ConsFactor
}