教你使用百度深度学习框架PaddlePaddle完成波士顿房价预测（新手向）

 

  首先，本文是一篇纯新手向文章，我自己也只能算是入门，有说错的地方欢迎大家批评讨论

目录

一、人工智能、机器学习、深度学习

二、PaddlePaddle（飞桨）

三、波士顿房价预测模型

数据处理

模型设计

训练配置

训练过程

模型保存

模型测试

四、小结

---

一、人工智能、机器学习、深度学习

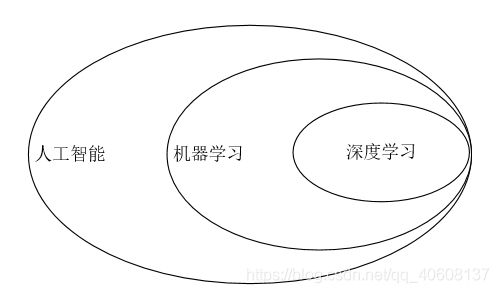
  近几年人工智能可以说是火的不能再火，大家可能会觉得人工智能=机器学习=深度学习，其实不是这样的，这三个概念是一种包含的层层深入的关系。

  机器学习：专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。 它是人工智能的核心，是使计算机具有智能的根本途径。

  深度学习：深度学习是机器学习的分支，是一种以人工神经网络为架构，对数据进行表征学习的算法。

其实这么说大家可能也没听懂，不过这并不是我们今天的主题，大致了解一下就好。

二、PaddlePaddle（飞桨）

  大家平常接触到的深度学习框架可能有PyTorch、TensorFlow等等，今天的飞桨是百度研制的一款开源的深度学习框架，个人认为可以满足日常学习，另外，百度还配套有专门的线上实训平台aistudio，提供了丰富的课程以及免费的GPU（百度打钱，hahaha）十分良心。一下是PaddlePaddle的API以及GitHub地址，大家没事可以多看看挺有意思的。

三、波士顿房价预测模型

  波士顿房价预测项目是一个经典的入门级项目，我们认为波士顿地区的房价受多种因素影响（人均犯罪率，一氧化氮浓度等等），我们收集了房价随各种因素变化而变化的数据，现在我们需要使用计算机根据这些数据来设计一个房价受各因素影响而变化的模型。对于预测问题，可以根据预测输出的类型是连续的实数值，还是离散的标签，区分为回归任务和分类任务。因为房价是一个连续值，所以房价预测显然是一个回归任务。下面我们尝试用最简单的线性回归模型解决这个问题，并用神经网络来实现这个模型。

  构建神经网络的基本步骤如下图所示，我们将会用飞桨框架来搭建这个项目，并对其中的基本概念进行解释

数据处理

  数据处理包含五个部分：数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数。数据预处理后，才能被模型调用，可以说一个好的数据处理方式是优秀网络搭建的基石。

  我们使用的数据的格式是一些506*14的数字

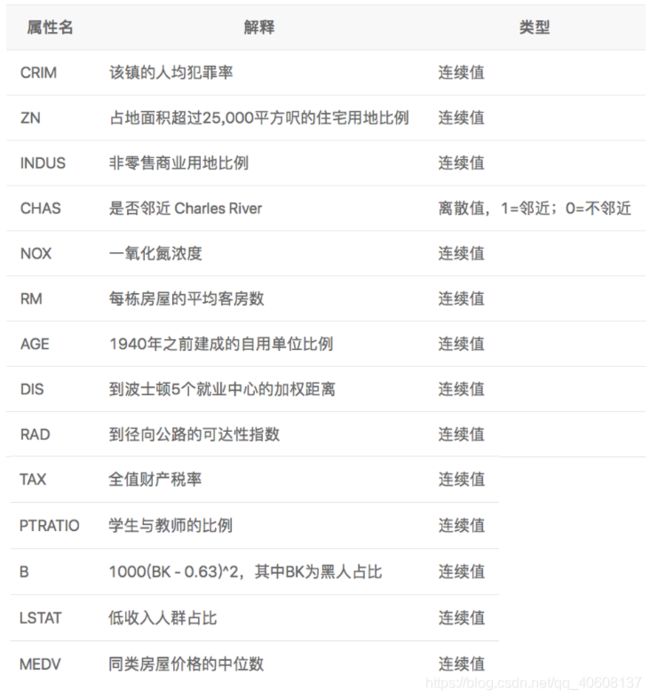
其中前13列代表影响因素，最后一列是房价（影响因素具体如下）

         

话不多说直接上代码

数据导入

# 导入需要用到的package
# 加载飞桨、Numpy和相关类库
import paddle
import paddle.fluid as fluid
import paddle.fluid.dygraph as dygraph
from paddle.fluid.dygraph import Linear
import numpy as np
import os
import random
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
print(data)

# 在文件里的数据已经转化为Python中的ndarry格式了
[6.320e-03 1.800e+01 2.310e+00 ... 3.969e+02 7.880e+00 1.190e+01]

数据形状变换

在原始文件中，我们的数据都是连在一起的是个一维的，我们不能区分出自变量（影响因素x）和因变量（房价y）之间的界限，因此我们需要对这些数据进行形状变化，形成一个2维的矩阵，每行为一个数据样本（14个值），每个数据样本包含13个X（影响房价的特征）和一个Y（该类型房屋的均价）。

# 读入之后的数据被转化成1维array，其中array的第0-13项是第一条数据，第14-27项是第二条数据，以此类推.... 
# 这里对原始数据做reshape，变成N x 14的形式
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 
                 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])

# 查看数据
x = data[0]
# 打印x的形状
print(x.shape)
print(x)

输出：
(14,)
[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01
 4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00 2.400e+01]

数据集划分

我们需要将数据集划分成训练集和测试集，其中训练集用于确定模型的参数，验证集用于调节模型超参数（如多个网络结构、正则化权重的最优选择），测试集用于评判模型的效果。在本案例中，我们将80%的数据用作训练集，20%用作测试集，由于数据不多，网络简单，所以没有安排验证集。

# 将0.8作为训练集
ratio = 0.8
offset = int(data.shape[0] * ratio)
# 从数据开始到0.8的位置都是训练集部分
training_data = data[:offset]
#查看训练集大小
training_data.shape


输出：
(404, 14)

数据归一化处理

对每个特征进行归一化处理，使得每个特征的取值缩放到0~1之间。这样做有两个好处：一是模型训练更高效；二是特征前的权重大小可以代表该变量对预测结果的贡献度（因为每个特征值本身的范围相同）

# 计算train数据集每个影响因素的最大值，最小值，平均值
maximums, minimums, avgs = \
                     training_data.max(axis=0), \
                     training_data.min(axis=0), \
     training_data.sum(axis=0) / training_data.shape[0]

# 对数据进行归一化处理,并查看每一个影响因素中的最大值最小值和均值
for i in range(feature_num):
    print(maximums[i], minimums[i], avgs[i])
    data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])
    

输出十四列的最大值最小值均值：
0.9785367890017308 -0.021463210998269224 -1.2366345571319812e-18
0.8576732673267327 -0.14232673267326734 -2.6931152577540925e-17
0.6410350642051105 -0.35896493579488953 -1.09923071745065e-18
0.9133663366336635 -0.08663366336633646 9.364071674282725e-17
0.6980824471336023 -0.3019175528663977 -8.244230380879875e-19
0.4688428988520618 -0.5311571011479382 -4.1221151904399375e-19
0.366349379531156 -0.633650620468844 -3.0228844729892876e-18
0.7231389197081554 -0.27686108029184464 -3.0915863928299533e-18
0.7482780886784333 -0.2517219113215666 -3.022884472989288e-17
0.6536307075383947 -0.3463692924616053 2.1984614349013e-18
0.4227406783231515 -0.5772593216768486 -2.7480767936266252e-18
0.05191120077969154 -0.9480887992203084 1.5457931964149766e-18
0.7344108583043735 -0.2655891416956266 -3.29769215235195e-18
0.5738723872387239 -0.42612761276127614 4.259519030121269e-18

封装load data函数

就是将前几步合起来方便使用

def load_data():
    # 从文件导入数据
    datafile = './work/housing.data'
    data = np.fromfile(datafile, sep=' ')

    # 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数
    feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \
                      'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
    feature_num = len(feature_names)

    # 将原始数据进行Reshape，变成[N, 14]这样的形状
    data = data.reshape([data.shape[0] // feature_num, feature_num])

    # 将原数据集拆分成训练集和测试集
    # 这里使用80%的数据做训练，20%的数据做测试
    # 测试集和训练集必须是没有交集的
    ratio = 0.8
    offset = int(data.shape[0] * ratio)
    training_data = data[:offset]

    # 计算train数据集的最大值，最小值，平均值
    maximums, minimums, avgs = training_data.max(axis=0), training_data.min(axis=0), \
                                 training_data.sum(axis=0) / training_data.shape[0]

    # 对数据进行归一化处理
    for i in range(feature_num):
        #print(maximums[i], minimums[i], avgs[i])
        data[:, i] = (data[:, i] - avgs[i]) / (maximums[i] - minimums[i])

    # 训练集和测试集的划分比例
    training_data = data[:offset]
    test_data = data[offset:]
    return training_data, test_data

至此，我们数据处理已经告一段落了，接下来我们拿到数据看看处理结果

# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]

# 查看数据
print(x[0])
print(y[0])

输出结果：
[-0.02146321  0.03767327 -0.28552309 -0.08663366  0.01289726  0.04634817
  0.00795597 -0.00765794 -0.25172191 -0.11881188 -0.29002528  0.0519112
 -0.17590923]
[-0.00390539]

模型设计

模型设计带有一定的经验性，在这个项目里，我们采用线性的模型即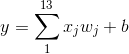,w，b就是我们需要求解的参数，我们不妨先给其一个随机的初始值

w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]
# 转化为13*1的向量，方便进行乘法操作
w = np.array(w).reshape([13, 1])

t=np.dot(x,w)

b = -0.2
z = t + b

这样我们的模型就设计好了，为了方便调用，我们实现一个类，成员变量是w，b，其中有前向计算（输入到输出）的方法

# 纯python
class Network(object):
    def __init__(self, num_of_weights):
        # 随机产生w的初始值
        # 为了保持程序每次运行结果的一致性，
        # 此处设置固定的随机数种子
        np.random.seed(0)
        self.w = np.random.randn(num_of_weights, 1)
        self.b = 0.
        
    def forward(self, x):
        z = np.dot(x, self.w) + self.b
        return z

以上模型的配置是用纯python来写的，实际上飞桨中的全连接层就可以实现线性回归这一模型

# 采用飞桨框架
class Regressor(fluid.dygraph.Layer):
    def __init__(self, name_scope):
        super(Regressor, self).__init__(name_scope)
        name_scope = self.full_name()
        # 定义一层全连接层，输出维度是1，激活函数为None，即不使用激活函数
        self.fc = Linear(input_dim=13, output_dim=1, act=None)
    
    # 网络的前向计算函数
    def forward(self, inputs):
        x = self.fc(inputs)
        return x

 

训练配置

# 定义飞桨动态图的工作环境
with fluid.dygraph.guard():
    # 声明定义好的线性回归模型
    model = Regressor("Regressor")
    # 开启模型训练模式
    model.train()
    # 加载数据
    training_data, test_data = load_data()
    # 定义优化算法，这里使用随机梯度下降-SGD
    # 学习率设置为0.01
    opt = fluid.optimizer.SGD(learning_rate=0.01, parameter_list=model.parameters())

在这里解释几个地方

• train()是父类的函数，表示训练，除此之外还会有eval(),表示评估。在执行时，train会进行前向传播和后向传播，而eval只会前向传播
• 关于后向传播，因为参数是我们随机生成的，难免会出错，在训练的时候我们定义一个loss函数来表示当前预测值跟真实值的差别，我们的追求是loss尽可能小，为了找到最小的loss我们可以找梯度（可以理解为导数）最小的点，那么如何来找最小的点呢，就需要使用优化器了

训练过程

训练的过程实际上就是不断地将预测值与实际值进行比较，找到loss最小的点的一个循环过程，因此我们采用两层循环来进行训练，其中内层循环负责对每次获得的数据进行计算反传梯度等，外层循环负责遍历数据集并用随机的方式取得训练的小批次

with dygraph.guard(fluid.CPUPlace()):
    EPOCH_NUM = 10   # 设置外层循环次数
    BATCH_SIZE = 10  # 设置batch大小
    
    # 定义外层循环，我们会对数据集遍历10次
    for epoch_id in range(EPOCH_NUM):
        # 在每轮迭代开始之前，将训练数据的顺序随机的打乱
        np.random.shuffle(training_data)
        # 将训练数据进行拆分，每个batch包含10条数据，一共就会有41个mini_batches,最后一个只有四个数据
        mini_batches = [training_data[k:k+BATCH_SIZE] for k in range(0, len(training_data), BATCH_SIZE)]
        # 定义内层循环
        for iter_id, mini_batch in enumerate(mini_batches):
            x = np.array(mini_batch[:, :-1]).astype('float32') # 获得当前批次训练数据
            y = np.array(mini_batch[:, -1:]).astype('float32') # 获得当前批次训练标签（真实房价）
            # 将numpy数据转为飞桨动态图variable形式
            house_features = dygraph.to_variable(x)
            prices = dygraph.to_variable(y)
            
            # 前向计算
            predicts = model(house_features)
            
            # 计算损失
            # 损失函数采用均方误差函数
            loss = fluid.layers.square_error_cost(predicts, label=prices)
            avg_loss = fluid.layers.mean(loss)
            # 计算20个样本打印一次loss
            if iter_id%20==0:
                print("epoch: {}, iter: {}, loss is: {}".format(epoch_id, iter_id, avg_loss.numpy()))
            
            # 反向传播
            avg_loss.backward()
            # 最小化loss,更新参数
            opt.minimize(avg_loss)
            # 清除梯度
            model.clear_gradients()
    # 保存模型
    fluid.save_dygraph(model.state_dict(), 'LR_model')

输出：
epoch: 0, iter: 0, loss is: [0.2819261]
epoch: 0, iter: 20, loss is: [0.09325473]
epoch: 0, iter: 40, loss is: [0.31836104]
epoch: 1, iter: 0, loss is: [0.06697255]
epoch: 1, iter: 20, loss is: [0.14381303]
epoch: 1, iter: 40, loss is: [0.02925108]
epoch: 2, iter: 0, loss is: [0.03091546]
epoch: 2, iter: 20, loss is: [0.17063697]
epoch: 2, iter: 40, loss is: [0.1874596]
epoch: 3, iter: 0, loss is: [0.12090156]
epoch: 3, iter: 20, loss is: [0.0605287]
epoch: 3, iter: 40, loss is: [0.06634661]
epoch: 4, iter: 0, loss is: [0.06475429]
epoch: 4, iter: 20, loss is: [0.06778971]
epoch: 4, iter: 40, loss is: [0.32411507]
epoch: 5, iter: 0, loss is: [0.08117181]
epoch: 5, iter: 20, loss is: [0.06476147]
epoch: 5, iter: 40, loss is: [0.00810404]
epoch: 6, iter: 0, loss is: [0.02915803]
epoch: 6, iter: 20, loss is: [0.10254985]
epoch: 6, iter: 40, loss is: [0.07706425]
epoch: 7, iter: 0, loss is: [0.10288523]
epoch: 7, iter: 20, loss is: [0.12237016]
epoch: 7, iter: 40, loss is: [0.0179625]
epoch: 8, iter: 0, loss is: [0.03814844]
epoch: 8, iter: 20, loss is: [0.1533469]
epoch: 8, iter: 40, loss is: [0.0867041]
epoch: 9, iter: 0, loss is: [0.08161684]
epoch: 9, iter: 20, loss is: [0.09394293]
epoch: 9, iter: 40, loss is: [0.24671933]

我们可以很明显看到loss在不断减小，我们的工作是有效果的！

模型保存

  我们可以将我们训练好的模型参数保存，下次直接拿来使用

# 定义飞桨动态图工作环境
with fluid.dygraph.guard():
    # 保存模型参数，文件名为LR_model
    fluid.save_dygraph(model.state_dict(), 'LR_model')
    print("模型保存成功，模型参数保存在LR_model中")

模型测试

模型测试其实跟训练类似，不过少了反向更新梯度

# 从测试集中加载数据
def load_one_example(data_dir):
    f = open(data_dir, 'r')
    datas = f.readlines()
    # 选择倒数第10条数据用于测试
    tmp = datas[-10]
    tmp = tmp.strip().split()
    one_data = [float(v) for v in tmp]

    # 对数据进行归一化处理
    for i in range(len(one_data)-1):
        one_data[i] = (one_data[i] - avg_values[i]) / (max_values[i] - min_values[i])

    data = np.reshape(np.array(one_data[:-1]), [1, -1]).astype(np.float32)
    label = one_data[-1]
    return data, label

# 加载模型进行预测
with dygraph.guard():
    # 参数为保存模型参数的文件地址
    model_dict, _ = fluid.load_dygraph('LR_model')
    model.load_dict(model_dict)
    model.eval()

    # 参数为数据集的文件地址
    test_data, label = load_one_example('./work/housing.data')
    # 将数据转为动态图的variable格式
    test_data = dygraph.to_variable(test_data)
    results = model(test_data)

    # 对结果做反归一化处理，即还原成之前的数值
    results = results * (max_values[-1] - min_values[-1]) + avg_values[-1]
    print("Inference result is {}, the corresponding label is {}".format(results.numpy(), label))

Inference result is [[17.563766]], the corresponding label is 19.7

我们可以看出，预测输出跟真实输出十分接近。

四、小结

我们使用飞桨框架，搭建了一个只有一层全连接层的网络，了解了深度学习的五步骤，但是每个步骤都有极大的研究空间，大家有兴趣可以选择一个深度学习的方向进行研究，学到更多的知识！