1.1 JML语言理论基础梳理
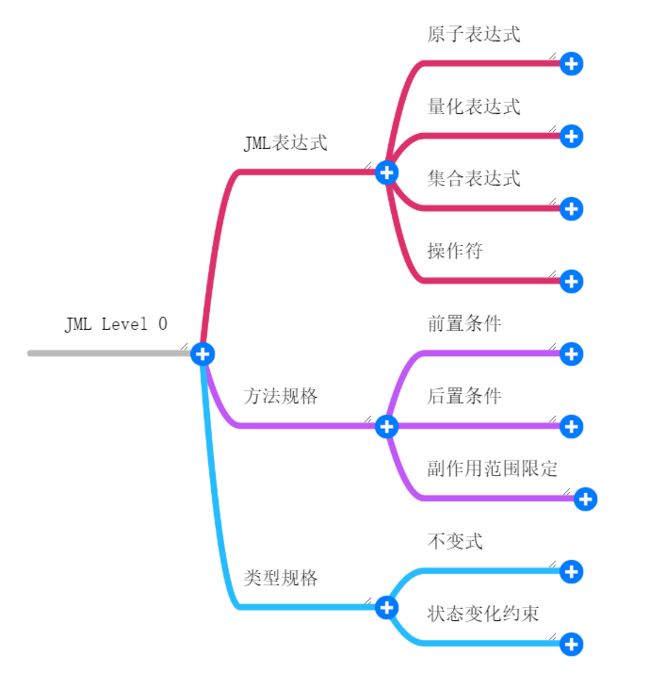
先上一张思维导图,这是JML level 0下主要的语法
由于JML手册中已经给出了详尽的规范,所以此处只叙述一下个人的理解:
一般而言看JML可以先看他的类型规格,尤其是所属的类有什么成员变量(容器不需要严格实现,但是成员的分布需要了解),不变式或者状态约束可以暂时跳过;然后针对每个方法,可以先看其正常状况下的ensures,因为这个是方法的主要功能!然后通篇读完所有的类与方法之后,再开始从较为底层的方法开始严格按照JML写!
1.2 JML工具链
①Junit4 手动单元测试
②OpenJML 检查JML的语法
③SMT Solver 检查JML与代码的符合性
④JMLUnitNG 根据JML生成测试样例并进行检验
总的来讲后三个工具链报错巨多,而且并不是很智能,详尽分析请看下文
2 JML验证工具
2.1 openJML
openJML用于对JML语法进行检查
指令:java -jar
注意-check是针对某一个java文件进行检查,而-dir则会连带其整个目录进行检查
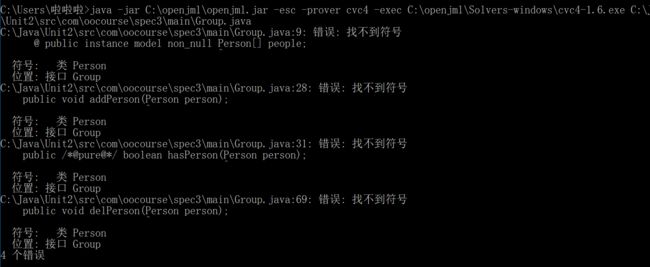
仅对Group.java的检查
可以发现找到的错误均与Person有关,于是我们连带整个目录进行检查
就没有任何错误
2.2 SMT Solver
指令:java -jar
SMT Solver已经包含在下载的openJML里面
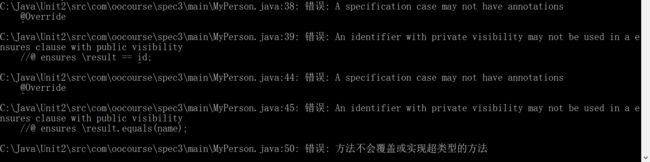
分析两个报错:
①发现其对@Override的标签也会报错,目测是由于无法识别@Override的含义
②在ensure语句中不该出现私有变量
2.3 JMLUnitNG
指令:java -jar
注意需要将诸如new HashMap<>()中<>内的内容补全
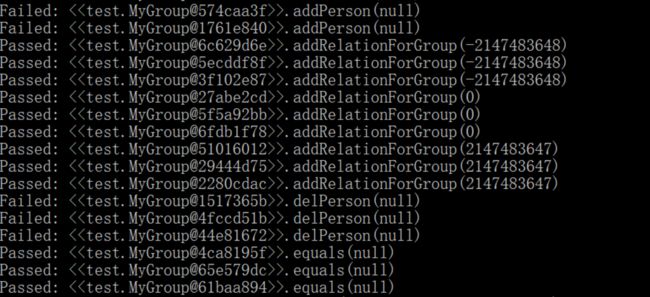
可以看到生成的测试样例取得都是极端值、0、null等等,并且不能准确识别requires
所以简而言之就是,这款工具还相当的简陋,离实际应用相距甚远
4 模型构建策略
写在前面:一定要弄明白模型的整体目的 再仔细看JML!!!
由于三次作业在迭代过程中,仅增加了一些函数,所以直接从第三次作业分析
4.1 数据结构的选择
首先需要明确:JML类型规格中给出的容器,仅供参考,不一定需要实现
本次作业中由于Person和Group都有独一无二的id,所以选择HashMap作为People和Groups的容器是非常合适的,ArrayList的底层实现是数组,查找效率不高,而HashMap作为散列表查找的时间复杂度近乎o(1)
在和同学交流过程中,得知:
① 有人会根据函数需要遍历还是查找来选择ArrayList和HashMap,个人认为如果确实有这样的区分度的话,是一个很不错的想法,但是我应该所有的容器都采用HashMap,因为我也观察过大部分函数都是需要查找,这样不会超时也较为简单
② 有人全部使用ArrayList导致强测TLE,后来我与其共同分析,在queryNameRank()中时间复杂度过高!
4.2 算法选择
4.2.1 缓存法
针对查询年龄平均、方差等等此类功能,采用缓存法需要在add和delete时做出极为小心的改动,并且认真阅读JML,因为部分数据与直觉不符,但是可以极大地节约时间
然而,第二次作业中一开始,我非常轻率的直接严格按照JML用二重循环写,直到在测试过程中发现会超时,几乎全部重构的修改了函数,才避免了TLE
4.2.2 并查集
iscircle()和queryBlockSum()都可以用并查集非常轻松地解决,其中iscircle()时间复杂度为o(1),queryBlockSum()时间复杂度为o(n)
此外并查集有两个可以进行优化的地方:
① 路径压缩
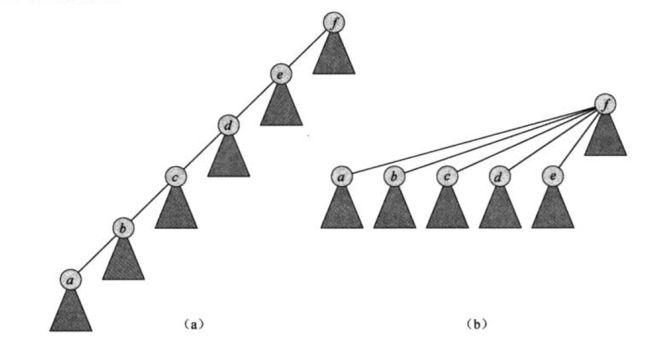
由于使用树来存储一个集合内的所有元素,而树根则是该集合的代表,如果不路径压缩,时间复杂度为o(height),而路径压缩是一种启发式的优化手段,因为事实上可以把所有的元素(除树根)直接连到树根上,从而实现o(1)的查询时间复杂度
P.S. 图片取自《算法导论》(原书第3版)作者: Thomas H.Cormen / Charles E.Leiserson / Ronald L.Rivest / Clifford Stein
② 按秩分配
注意到并查集在合并两个集合时,将一棵树的树根挂到另一棵树根上,为了使得树高(height)尽量低,一般选择将低一些的树挂到另一棵树上
此算法我并未实现,(实际上实现起来相当简单),但是考虑到使用并查集+路径压缩已经可以实现相当高的查找效率,就不增加代码的复杂性
4.2.3 Dijkstra算法&Tarjan算法
针对queryMinPath()采用Dijkstra算法,由于不是算法课不详尽介绍了,但是注意求最小的路径估计时,可以采用java自带的PriorityQueue,其底层采用堆实现,可以显著降低时间复杂度
针对queryStrongLinked(),采用Tarjan算法,其本质是求点双联通分量,但是要注意:离散数学中两点一线也算点双联通,但是根据JML此处不算,所以采用Tarjan算法之后要加以特判排除两点一线情况
5 bug与修复情况
5.1 自己的bug:
仅第二次作业互测中被发现1个bug
原因分析:
浅层原因:
第二次作业中iscircle()函数可以通过并查集快速实现,并查集主要有3个操作构成:
新建集合:MAKE-SET(v),
寻找给定元素所在集合的根:FIND-SET(v),
合并两个集合:UNION(v, u)
而对于两个集合的合并应当写成:
UNION( FIND-SET(v), FIND-SET(u) )
即寻找两个集合的根节点并且使得这两个根节点成为父子节点,而因为第一次写并查集误写成UNION(v, FIND-SET(u)),从而导致部分连接信息丢失,但是强测中并未被hack,可能是由于强测中图的连通性过高,部分信息的缺失不足以导致iscircle()判断的
深层原因:
本次作业依旧采用自动测评的方式进行测试,方法如下:
①利用python脚本实现一个生成器,随机输出指令并且维护指令计数器与已给出id的列表
②利用git diff功能与同学代码对拍
本次作业由于对于一组给定的指令,结果必然完全一致,所以对拍即可实现比对,比前两次作业进行逻辑验证方便许多
然而,问题即发生在python脚本的生成器,由于版本管理失误,我使用了旧版的生成器,其不会生成iscircle()指令,从而导致代码测试的覆盖不全
注:
a.并查集的三个操作引用 《算法导论》(原书第3版)作者: Thomas H.Cormen / Charles E.Leiserson / Ronald L.Rivest / Clifford Stein
b.感谢hjw同学分享的生成器以及他在OO课程上对我的其他帮助
5.2 互测发现的bug
第1、3次互测整个room均未发现任何bug
第2次互测中发现三个bug,均为WRONG ANSWER
原因分析:
对于queryAgeMean()和queryAgeVar()这两个函数,JML中均给出关于整除的严格说明,但是有同学忽略了这一点,以至于在特定数据下会出现相差1的错误
6 心得体会
a. 一定要注意JML中,方法规格的要求是强制性的,但是对于类的成员数据类型要求却是非强制的,意味着:JML规格中可能给出的静态数组,而你可以用任意容易诸如HashMap去实现,以提高性能