《机器学习实战》 第九章 树回归

      线性回归模型需要拟合所有样本（除局部加权线性回归外），当数据拥有众多特征且特征间关系十分复杂时，构建全局模型就显得太难了。一种可行的方法是将数据集切分成很多份易建模的数据，然后利用线性回归技术建模。如果首次切分后仍难以拟合线性模型就继续切分，在这种切分模式下，树结构和回归法相当有用。

       CART（Classification And Regression Trees，分类回归树）算法，即可用于分类，也可用于回归。其中的树剪枝技术用于防止树的过拟合。

本书第三章使用决策树进行分类。决策树不断将数据切分成小数据集，直到所有目标变量完全相同，或者数据不能再切分为止。决策树是一种贪心算法，它要在给定的时间内做出最佳选择，但不关心能否达到全局最优。

构建决策树算法，常用到的是三个方法: ID3, C4.5, CART.
三种方法的区别在于划分树的分支的方式:
       （1） ID3 是信息增益分支
       （2） C4.5 是信息增益率分支
       （3） CART 是 GINI 系数分支

       CART 和 C4.5 之间主要差异在于分类结果上，CART 可以回归分析也可以分类，C4.5 只能做分类；C4.5 子节点是可以多分的，而 CART 是无数个二叉子节点；以此拓展出以 CART 为基础的 “树群” Random forest ， 以 回归树 为基础的 “树群” GBDT 。

       而之前在第3章中使用的树构建算法是 ID3 。ID3 的做法是每次选取当前最佳的特征来分割数据，并按照该特征的所有可能取值来切分。也就是说，如果一个特征有 4 种取值，那么数据将被切分成 4 份。一旦按照某特征切分后，该特征在之后的算法执行过程中将不会再起作用，所以有观点认为这种切分方式过于迅速。除了切分过于迅速外， ID3 算法还存在另一个问题，那就是它不能直接处理连续型特征。只有事先将连续型特征转换成离散型，才能在 ID3 算法中使用。但这种转换过程会破坏连续型变量的内在性质。

       另外一种树构建方法是二分切分法，即每次把数据集切分成两份。如果数据的某特征值等于切分所要求的值，那么这些数据就进入树的左子树，反之则进入树的右子树。使用二元切分法则易于对树构造过程进行调整以处理连续型特征。具体的处理方法是: 如果特征值大于给定值就走左子树，否则就走右子树。另外，二分切分法也节省了树的构建时间，但这点意义也不是特别大，因为这些树构建一般是离线完成，时间并非需要重点关注的因素。

       CART 是十分著名且广泛记载的树构建算法，它使用二元切分来处理连续型变量，对其稍作修改就可处理回归问题。CART算法也使用一个字典来存储树的数据结构，该字典含：
    待切分的特征
    待切分的特征值
    右子树。不需切分时，也可是单个值

    左子树。与右子树类似。

       CART可构建两种树：回归树（regression tree），其每个叶节点包含单个值；模型树（model tree），其每个叶节点包含一个线性方程。回归树与分类树的思路类似，但是叶节点的数据类型不是离散型，而是连续型。

1、将CAPT算法用于回归

       回归树假设叶节点是常数值，这种策略认为数据中的复杂关系可用树结构来概括。为了构建以分段常数为叶节点的树，需要度量数据的一致性。使用ID3算法构建的决策树进行分类，会在给定节点时计算数据的混乱度。计算连续性数值的混乱度是非常简单的，首先计算所有数值的均值，然后计算每条数据的值到均值的差值。为了对正负差值同等看待，一般使用绝对值或平方值来代替上述差值。这里使用的是总方差（平方误差的总值），总方差=均方差*样本数。

1.1 构建树

       首先要找到数据集切分的最佳位置，在书中使用函数chooseBestSplit()函数切分数据集。给定误差计算方法，该函数寻找数据集上的最佳二元切分方式，一旦停止切分会生成一个叶节点。它遍历所有的特征及其可能的取值来找到使误差最小化的切分阈值。函数的伪代码如下：

切分停止的三个条件：
（1）剩余特征值的数目为1；
（2）如果切分数据集后的误差提升不大，不应进行切分操作，而直接创建叶节点；

（3）两个切分后的子集中的一个的大小小于用户定义的参数tolN时；

1.2 树剪枝

       一棵树如果节点过多，表明该模型可能对数据进行了 “过拟合”。通过降低决策树的复杂度来避免过拟合的过程称为剪枝（pruning）。在chooseBestSplit()中提前终止条件，实际上是一种所谓的预剪枝（prepruning）操作。另一种剪枝需要使用测试集和训练集，称为后剪枝（postpruning）。

       预剪枝(prepruning)：顾名思义，预剪枝就是及早的停止树增长，在构造决策树的同时进行剪枝。所有决策树的构建方法，都是在无法进一步降低熵的情况下才会停止创建分支的过程，为了避免过拟合，可以设定一个阈值，熵减小的数量小于这个阈值，即使还可以继续降低熵，也停止继续创建分支。但是这种方法实际中的效果并不好。

       后剪枝(postpruning)：决策树构造完成后进行剪枝。剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，熵的增加量是否小于某一阈值。如果确实小，则这一组节点可以合并一个节点，其中包含了所有可能的结果。合并也被称作 塌陷处理 ，在回归树中一般采用取需要合并的所有子树的平均值。后剪枝是目前最普遍的做法。函数prune()的伪代码如下：

2、模型树

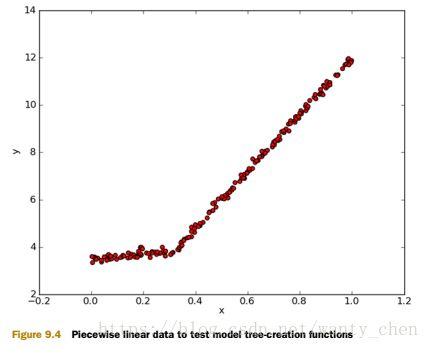
       用树来对数据建模，除了把叶节点简单地设定为常数值之外，还有一种方法是把叶节点设定为分段线性函数，这里所谓的分段线性（piecewise linear）是指模型由多个线性片段组成。模型树的可解析性是它优于回归的特点之一，它还具有更高的预测准确度。如图所示的数据，使用两条直线进行拟合的效果明显比用一条直线进行拟合的效果好。

                                    

       为判断模型树、回归树和一般的回归方法，哪个模型最好，书中使用相关系数R^2 来衡量。R^2 判定系数就是拟合优度判定系数，它体现了回归模型中自变量的变异在因变量的变异中所占的比例。R^2 的值越接近 1.0 越好。