java数据结构源码解读——优先队列
优先队列就是PriorityQueue,每次插入都能以O(logN)的时间整理好元素,然后让最大/最小值处于根位置,从而能够以O(1)时间访问最大/最小值。如果父节点的值总是大于等于子节点的值,那么称为大根堆(根是最大值),反之,如果父节点总是小于等于子节点的值,那么称为小根堆。
著名的TopK算法就是以此为基础实现的。
让我们探索一下jdk的优先队列。
首先观察字段:
private static final long serialVersionUID = -7720805057305804111L;//序列化Id
private static final int DEFAULT_INITIAL_CAPACITY = 11;//默认容量=11
transient Object[] queue;//这个就是最重要的存储数据的数组了
int size;//元素个数
private final Comparator comparator;//构造时候的比较器
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;//最大的数组大小我们可以看出由于相对有序性,是需要比较器来维护顺序的。而且实际上使用数组queue实现的堆结构,而且与ArrayList类似,优先队列有size和Capacity,说明有一定的扩容规则。
接下来看看构造器是什么样子:
public PriorityQueue() {//默认的无参构造器,容量11,比较器null
this(DEFAULT_INITIAL_CAPACITY, null);
}
public PriorityQueue(int initialCapacity) {//给出初始容量的构造
this(initialCapacity, null);
}
public PriorityQueue(Comparator comparator) {//给出比较器的构造
this(DEFAULT_INITIAL_CAPACITY, comparator);
}
public PriorityQueue(int initialCapacity,
Comparator comparator) {
// Note: This restriction of at least one is not actually needed,
// but continues for 1.5 compatibility
//(上面不是我的注释)同时给出比较器和容量的构造器,要求至少容量为1
if (initialCapacity < 1)
throw new IllegalArgumentException();
this.queue = new Object[initialCapacity];
this.comparator = comparator;
}
public PriorityQueue(Collection c) {//获取元素型
if (c instanceof SortedSet) {
SortedSet ss = (SortedSet) c;
this.comparator = (Comparator) ss.comparator();
initElementsFromCollection(ss);
}
else if (c instanceof PriorityQueue) {
PriorityQueue pq = (PriorityQueue) c;
this.comparator = (Comparator) pq.comparator();
initFromPriorityQueue(pq);
}
else {
this.comparator = null;
initFromCollection(c);
}
}
public PriorityQueue(PriorityQueue c) {
this.comparator = (Comparator) c.comparator();
initFromPriorityQueue(c);
}
public PriorityQueue(SortedSet c) {
this.comparator = (Comparator) c.comparator();
initElementsFromCollection(c);
}优先队列的比较器比较多。
当我们插入一个元素时:
public boolean add(E e) {
return offer(e);
}
public boolean offer(E e) {
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)
grow(i + 1);//扩容
siftUp(i, e);//堆有序化过滤
size = i + 1;
return true;
}
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// overflow-conscious code
if (newCapacity - MAX_ARRAY_SIZE > 0)
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}别的不用管,就是两个极其重要的操作:
grow:数组扩张
siftUp:维护堆性质
第二个一会再说,先看扩容规则,能十分清晰地看出大概是:
如果原数组capacity<64,那么 cap=2*cap+2;否则cap=1.5cap。
堆化是最重要的操作,这里面我们可以简单的称siftUp为“上移”操作(算法导论称上浮)。
先观察代码:
private void siftUp(int k, E x) {
if (comparator != null)
siftUpUsingComparator(k, x, queue, comparator);//以此函数为例说明过程,下面同
else
siftUpComparable(k, x, queue);
}
private static void siftUpUsingComparator(
int k, T x, Object[] es, Comparator cmp) {
while (k > 0) {
int parent = (k - 1) >>> 1;//父节点下标:(k-1)/2
Object e = es[parent];//交换上浮
if (cmp.compare(x, (T) e) >= 0)
break;//默认小顶堆,不满足交换条件就退出
es[k] = e;
k = parent;
}
es[k] = x;
} 下面说明一下这个过程,可能有的人不太了解堆的性质:
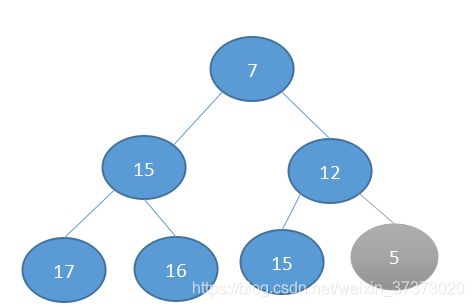
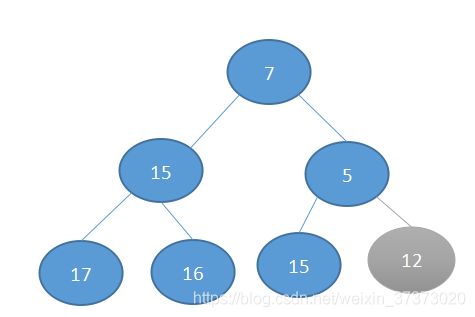
5是新加入的顶点,那么第一步就是交换12 5:
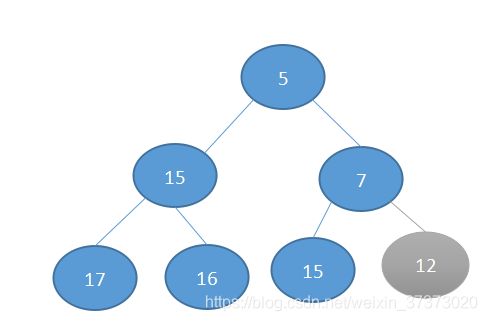
第二步,交换7 5:
此时已经到达了根部,无法继续交换,所以,“上移”过程结束。
与之相匹配的是poll一个元素出来,这个元素一定是插入的元素里面最小的(最大的)。
那么观察一下
public E poll() {
final Object[] es;
final E result;
if ((result = (E) ((es = queue)[0])) != null) {
modCount++;
final int n;
final E x = (E) es[(n = --size)];//弹出下标为0的元素,末尾元素放置到0,并且开始下移
es[n] = null;//尾元素置为null,size减小1
if (n > 0) {
final Comparator cmp;
if ((cmp = comparator) == null)
siftDownComparable(0, x, es, n);//下移操作
else
siftDownUsingComparator(0, x, es, n, cmp);
}
}
return result;
}由于堆的相对有序性,poll就是弹出下标为0的元素,然后为了维护有序性,从下标为0的地方开始“下移”。
代码:
private static void siftDownUsingComparator(
int k, T x, Object[] es, int n, Comparator cmp) {
// assert n > 0;
int half = n >>> 1;//为了保证k(作为父节点)不会出现在最后一层(叶子),需要k 0)
c = es[child = right];//选取左右两个孩子中较小的那个
if (cmp.compare(x, (T) c) <= 0)
break;//如果发现已经父节点小于两个孩子,那么退出,否则交换
es[k] = c;
k = child;
}
es[k] = x;
}
用刚才的图说明一下:
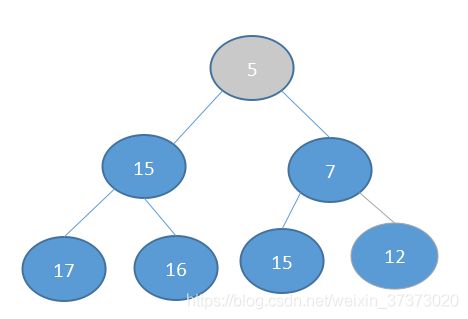
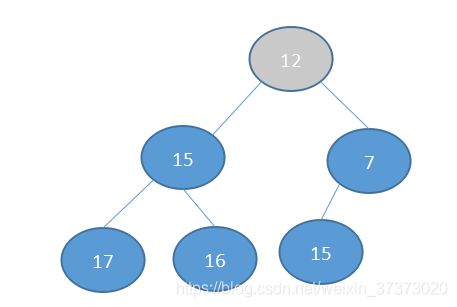
现在元素5即将被弹出,所以根据程序,把尾元素移到堆顶去。
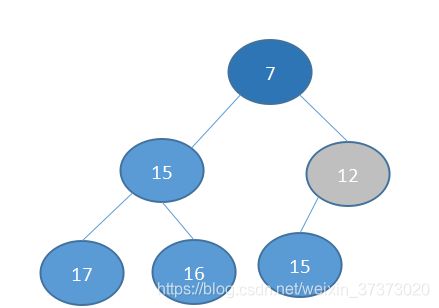
根据堆的法则(最小堆),将会与7交换:
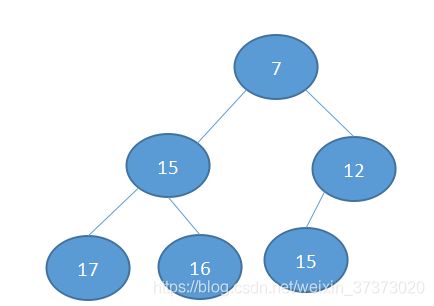
然后发现已经满足了,就不再交换。
这两个过程和我们课本上的几乎没有区别,可以说正是有了理论基础,才有了优先队列实现的良好性能。
最后看一个课本上的“堆化”操作。
private void heapify() {
final Object[] es = queue;
int n = size, i = (n >>> 1) - 1;
final Comparator cmp;
if ((cmp = comparator) == null)
for (; i >= 0; i--)//从倒数第二层开始每个节点都下“下移”一次
siftDownComparable(i, (E) es[i], es, n);
else
for (; i >= 0; i--)
siftDownUsingComparator(i, (E) es[i], es, n, cmp);
}这个操作主要是用来把传入的数组(集合)转化成堆形式。
综上所述,除了一个“小容量2*cap+2,大容量1.5cap”,其他的还是几乎与课本上的一致。