算法刷题5【剑指offer系列之树】

2020.06.04

1、前序中序重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。
思路：前序遍历根左右，中序遍历左根右，因此前序数组的第一个元素pre[0]就是根，可以按照这个根将中序数组分成左右两个部分。然后root.left在左部分，root.right在右部分。
（1）根据pre[0]新建结点，这个结点就是root
（2）遍历中序数组，找到root，然后开始递归；递归出口就是in.length==0||pre.length == 0
（3）返回root

注意copyOfRange是左闭右开的

public class ReconstructionTree {

    public TreeNode reConstructBinaryTree(int [] pre, int [] in) {
        //base case
        if (pre==null||pre.length==0||in==null||in.length==0){
            return null;
        }else {
            TreeNode root=new TreeNode(pre[0]);
            //中序遍历寻找根
            for (int i=0;i<in.length;i++){
                if (root.val==in[i]){
                    //注意copyOfRange是左闭右开的
                    root.left=reConstructBinaryTree(Arrays.copyOfRange(pre,1,i+1),
                            Arrays.copyOfRange(in,0,i));
                    root.right=reConstructBinaryTree(Arrays.copyOfRange(pre,i+1,pre.length-1)
                    ,Arrays.copyOfRange(in,i+1,in.length));
                }
            }
            return root;
        }

    }
}

2、判断树B是否为A的子树

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）
思路：
（1）需要在A 树中查找到和B的根节点相同的结点，这个结点下面存在的子树就有可能和树B一样，查找的过程可以使用递归实现
（2）判断以第一步在A树中找到的结点为根的A1树是否存在子树和B树相等：注意递归的终止条件

(1） B树为空说明判断成功（A1树有可能还不为空的,因为子树可能是中间的部分）
（2） A1树为空但是B树不为空则判断失败

需要注意的是在树的取值操作之前要先判断是否为空，避免空指针异常。

public class HasSubtree {

    /**
     * 1、递归查找到和B的根节点相同的结点
     * 树的操作要一直想着指针不能为空
     *
     * @param root1
     * @param root2
     * @return
     */
    public boolean HasSubtree(TreeNode root1, TreeNode root2) {
        if (root1==null||root2==null){
            return false;
        }
        boolean res = false;
        if (root1 != null && root2 != null) {
            if (root1.val == root2.val) {
                res = judge(root1, root2);
            }
            //判断A的左树
            if (!res) {
                res = HasSubtree(root1.left, root2);
            }
            //判断A的右子树
            if (!res) {
                res = HasSubtree(root1.right, root2);
            }

        }
        return res;
    }

    /**
     * 2、判断A1树的子树和B树是否相等：注意递归的终止条件
     * （1） B树为空说明判断成功（A1树有可能还不为空的）
     * （2） A1树为空但是B树不为空则判断失败
     *
     * @param root1
     * @param root2
     * @return
     */
    private boolean judge(TreeNode root1, TreeNode root2) {
        if (root1 == null && root2 != null) {
            return false;
        }
        if (root2 == null) {
            return true;
        }
        if (root1.val != root2.val) {
            return false;
        }
        return judge(root1.left, root2.left) && judge(root1.right, root2.right);
    }
}

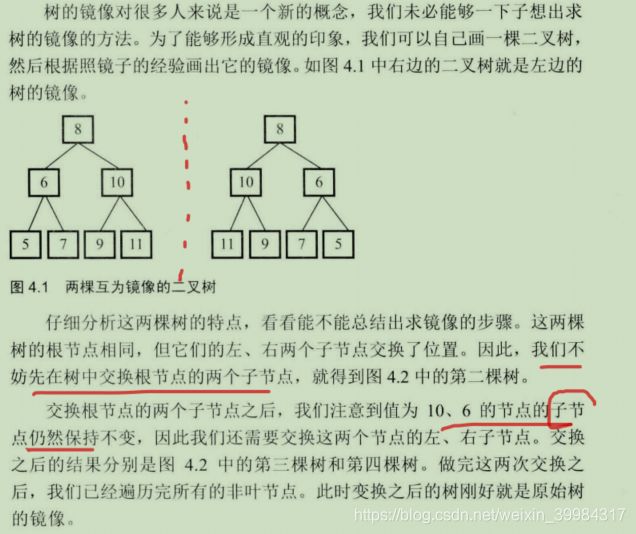
3、操作给定的二叉树，将其变换为源二叉树的镜像

思路：核心思想就是遍历树的同时如果有子结点，则交换左右子结点。可以采用任何一种遍历方式，最简单的就是前序递归直接搞定。

public class Mirror {

    /**
     * 核心：遍历的同时，如果有左右子结点，则交换
     *
     * @param root
     */
    public void Mirror(TreeNode root) {
        if (root == null) {
            return;
        }
        //说明是叶子节点
        if (root.left == null && root.right == null) {
            return;
        }
        //注意不是说左右孩子都有才能交换
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        if (root.left != null) {
            Mirror(root.left);
        }
        if (root.right != null) {
            Mirror(root.right);
        }
    }

    /**
     * 非递归：可以采用层次遍历:只要是遍历树就可以了
     * @param root
     */
    public void Mirror1(TreeNode root) {
        if (root==null){
            return;
        }
        ArrayDeque<TreeNode> queue=new ArrayDeque<>();
        TreeNode node=null,temp=null;
        queue.offer(root);
        while (!queue.isEmpty()){
            node=queue.poll();
            temp=node.left;
            node.left=node.right;
            node.right=temp;
            if (node.left!=null){
                queue.offer(node.left);
            }
            if (node.right!=null){
                queue.offer(node.right);
            }
        }
    }

}

2020.06.06

4、从上往下打印出二叉树的每个节点，同层节点从左至右打印。

思路：就是树的层次遍历

public class PrintFromTopToBottom {

    /**
     * 树的层次遍历
     * @param root
     * @return
     */
    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        ArrayList<Integer> res=new ArrayList<>();
        ArrayDeque<TreeNode> queue=new ArrayDeque<>();
        if (root==null){
            return res;
        }
        queue.offer(root);
        TreeNode cur=null;
        while (!queue.isEmpty()){
            cur=queue.poll();
            res.add(cur.val);
            if (cur.left!=null){
                queue.offer(cur.left);
            }
            if (cur.right!=null){
                queue.offer(cur.right);
            }
        }
        return res;
    }

扩展1：从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。

思路：这题就是层次遍历的变形。难点在于如何判断什么时候打印完一行，核心思路是使用两个变量记录当前行未打印的结点个数和下一行的结点个数，这样就能确保打印完一行。
（1）按层次遍历，每次循环remain–，表示当前行的结点数目减少1；如果左右孩子不为空，则左右孩子结点入队，同时nextCount++，表示下一层的结点数量变多
（2）每次循环都需要判断remain==0.如果remain=0，说明打印到当前行的最后一个结点，需要进行结算。

public class PrintLine {

    /**
     * 难点在于处理好什么时候新建ArrayList
     * @param pRoot
     * @return
     */
    ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> res = new ArrayList<>();
        ArrayDeque<TreeNode> queue = new ArrayDeque<>();
        if (pRoot == null) {
            return res;
        }
        queue.offer(pRoot);
        TreeNode node = null;
        //关键是使用两个变量记录
        int remain = 1, nextCount = 0;
        ArrayList<Integer> temp = new ArrayList<>();
        while (!queue.isEmpty()) {
            node = queue.poll();
            temp.add(node.val);
            remain--;
            if (node.left != null) {
                queue.offer(node.left);
                nextCount++;
            }
            if (node.right != null) {
                queue.offer(node.right);
                nextCount++;
            }
            //说明遍历完一层了，将ArrayList加到结果后需要新建
            if (remain == 0) {
                res.add(temp);
                //先置空，然后新建
                temp=null;
                temp=new ArrayList<>();
                remain = nextCount;
                nextCount = 0;
            }
        }
        return res;
    }

}

2020.06.07

扩展2 之字形打印二叉树

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。
思路：关键是使用两个栈保存不同层的结点（起点就是第1行，不是第0行）
(1)使用layer判断层数，初始为1，通过层数来判断奇偶
（2）和上题一样的思路，我们使用remain和nextCount来控制打印完一行，注意remain需要使用while循环来控制真正遍历完一整行
（3）如果layer为奇数，我们下面需要处理的是偶数行，偶数行从右到左打印，因此左孩子先入栈stack2同理：layer是偶数，我们需要处理奇数行，从左到右打印，因此右孩子先入栈stack1（这里易错）

public class PrintZ {

    public static void main(String[] args) {
        PrintZ z = new PrintZ();
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);
        ArrayList<ArrayList<Integer>> print = z.Print(root);
        System.out.println(print);
    }

    public ArrayList<ArrayList<Integer>> Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> res = new ArrayList<>();
        if (pRoot == null) {
            return res;
        }
        ArrayDeque<TreeNode> stack1 = new ArrayDeque<>();
        ArrayDeque<TreeNode> stack2 = new ArrayDeque<>();
        int layer = 1, remain = 1, nextCount = 0;
        stack1.push(pRoot);
        TreeNode node = null;
        ArrayList<Integer> temp = new ArrayList<>();
          //注意这里是或
        while (!stack1.isEmpty() || !stack2.isEmpty()) {
            if ((layer & 1) == 1) {
                //1、使用remain来控制一行的结束
                while (remain != 0) {
                    //2、说明是奇数层
                    node = stack1.pop();
                    remain--;
                    temp.add(node.val);
                    //2.1 下一行是偶数，偶数行从右到左打印，因此左孩子先入栈stack2
                    if (node.left != null) {
                        stack2.push(node.left);
                        nextCount++;
                    }
                    if (node.right != null) {
                        stack2.push(node.right);
                        nextCount++;
                    }
                }

            } else {
                while (remain != 0) {
                    //3、说明是偶数
                    node = stack2.pop();
                    remain--;
                    temp.add(node.val);
                    //3.1 下一行是奇数，奇数行从左到右打印，因此右孩子先入栈stack1
                    if (node.right != null) {
                        stack1.push(node.right);
                        nextCount++;
                    }
                    if (node.left != null) {
                        stack1.push(node.left);
                        nextCount++;
                    }

                }
            }
            //4、说明遍历完一行，需要层数+1，并且结算结果
            layer++;
            res.add(temp);
            temp = null;
            temp = new ArrayList<>();
            remain = nextCount;
            nextCount = 0;
        }
        return res;

    }
}

2020.06.08

5、判断是否为某二叉搜索树的后序遍历

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
思路:关键是分析得出二搜索树的最后一个结点是根结点，然后根据根节点划分，最后进行递归。
(1)后序遍历的最后一个是根节点，获取根节点
（2）根据根节点遍历数组，找到第一个大于根节点的位置，则该位置就是右子树的起点right（因为二叉搜索树的右子树大于根）
（3）从right开始继续遍历数组剩下的部分，如果遇到小于根节点的数字，则直接返回false，因为右子树不应该小于根
（4）根据上面right的划分点进行递归左右子树
（5）特别需要注意递归的退出条件，如果start==end，说明是叶子节点了，需要return true

 public boolean VerifySquenceOfBST(int[] sequence) {
        if (sequence == null || sequence.length == 0) {
            return false;
        }
        return judge(sequence, 0, sequence.length);
    }

    /**
     * 递归判断:特别注意递归的退出条件
     * @param sequence
     * @param
     * @return
     */
    private boolean judge(int[] sequence, int start, int end) {
        //start==end对应的是叶子结点，
        if (start==end){
            return true;
        }
        int root = sequence[end-1];
        //1、找到根节点的位置，即左子树都是小于根节点的
        //注意不用到len
        int i = start;
        for (; i < end - 1; i++) {
            if (sequence[i] > root) {
                break;
            }
        }
        //说明位置i就是根节点的划分（右子树的开始）
        int right = i;
        //2、如果右子树中存在小于根节点的树，则说明错误
        for (; right < end - 1; right++) {
            if (sequence[right] < root) {
                return false;
            }
        }
        //3、开始递归，注意需要end-1，因为最后一个是根节点，不属于右子树了
        return judge(sequence, start, i) && judge(sequence, i, end - 1);
    }
}

2020.06.10

6、打印出二叉树中结点值的和为输入整数的所有路径

输入一颗二叉树的根节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
思路：这题是经典题，字节跳动很喜欢考这题。其实就是前序遍历的应用，我们需要使用容器（list）保存好路径，关键是子结点回父结点的时候需要将子结点删除（因为无论符合，子结点都是先进入再判断）
（1）前序遍历：先将当前的节点进入list，然后target-root.val；
（2）如果target==0而且为叶子节点了，说明这是一条路径，需要结算结果
（3）如果不满足上面的条件，则需要递归左右子树
（4）递归结束返回前，都需要移除最后一个元素（这是最难的）回到递归之前的状态
注意点1：最后删掉的原因：因为你遍历到某一叶子节点的时候，不管该叶子结点是否合适都把该叶子节点的值加入list中 ，需要回溯到该叶子结点的父节点 ，再去判断子树的另一个叶子结点是否合适，所以刚刚加入list中的结点肯定要删除的。（需要root=null才会递归返回）

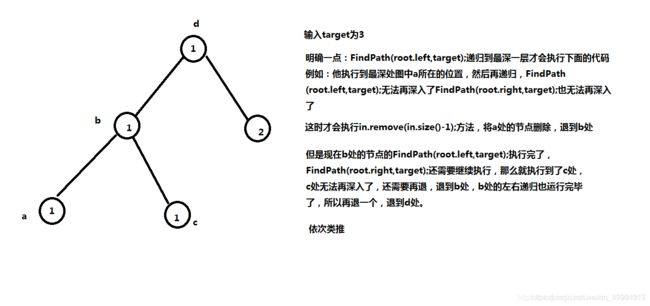
注意点2res每次加入list都要new的原因:如果直接添加，那么只有一个list，也只是说只有一条路径（对于多条路径来说，就是错的了）存在多条路径的情况，所以不再new的话，肯定出错。new ArrayList<>()这个构造方法直接传入一个list作为创建的list的值
注意点3为什么不需要将list清空呢？
原因:递归返回的时候list.remove(list.size()-1)会慢慢把lis移走，最后一局return不会把大递归结束，只会把当前递归结束。可以试一下像是10,5,12,4,7这种情况，递归到10,5,4的时候没有发现22的点，这时候就要把4去掉，再加入7才对，不然就会结果中变成10,5,4,7，这个4就是一个没去掉的叶子节点。
注意点4 需要将两个容器的初始化要放在函数的外面，否则每次递归的时候都会被初始化
**总结：**递归其实只需要考虑当前就好了，剩下的是子问题，内部也是采用相同的策略解决的。

public class FindPath {
    //两个初始化要放在函数的外面，否则每次递归的时候都会被初始化
    ArrayList<ArrayList<Integer>> res = new ArrayList<>();
    ArrayList<Integer> temp = new ArrayList<>();
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root, int target) {
        if (root == null) {
            return res;
        }
        temp.add(root.val);
        target -= root.val;
        //1、如果恰好到0说明找到路径和，且为叶子结点
        if (target == 0 && root.left == null && root.right == null) {
            res.add(new ArrayList<>(temp));
        } else {
            //2、不是叶子节点，继续找子结点
            FindPath(root.left, target);
            FindPath(root.right, target);
        }
        //3、返回之前需要将最后一个节点移除
        temp.remove(temp.size() - 1);
        //4、只是结束本次递归，不是结束整个递归
        return res;
    }
}

7、二叉搜索树转换成排序的双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。
思路：这题是典型的树的递归遍历的应用。其实这题应该就是我们在数据结构学的线索二叉树的转换方式，采用左前驱右后继的方式进行转换。因为是二叉搜索树，所以中序遍历的结果就是有序的。
所以核心就是：
（1）先将左子树转为双向链表，然后遍历找到左子树链表末尾，也就是左子树最大，然后连接root
（2）再将右子树转换成双向链表，root与之相连。
注意：在返回的时候需要判断左子树是否为空，如果为空，则返回root，因为root至少不为空，有可能只有root，有可能是root+right;
如果不为空，则返回左，这时候就是左根右，也就是整棵树。

public class Convert {
    public TreeNode Convert(TreeNode pRootOfTree) {
       //根节点为空
        if (pRootOfTree==null){
            return null;
        }
        //叶子节点
        if (pRootOfTree.left==null&&pRootOfTree.right==null){
           return pRootOfTree;
        }
        /*
        1、构造左子树，并返回头结点
         */
        TreeNode left = Convert(pRootOfTree.left);
        /*
            2、 找到左子树双链表的最后一个节点
         */
        TreeNode lastNode=left;
        //注意不是lastNode=null
        //处理right需要先保证lastNode不为null
        while (lastNode!=null&&lastNode.right!=null){
            lastNode=lastNode.right;
        }

        /*
        3、如果左子树不为空（鲁棒性）,则钩链（左根）
         */
        if (left!=null){
            lastNode.right=pRootOfTree;
            pRootOfTree.left=lastNode;
        }
        /*
        4、构造右子树
         */
        TreeNode right=Convert(pRootOfTree.right);
        /*
        5、如果右子树链表不为空，则加到根节点的后面
         */
        if (right!=null){
            pRootOfTree.right=right;
            right.left=pRootOfTree;
        }
        /*
        6、返回的时候需要判断有无左子树（右子树不用，因为是左根右）
         */
        if (left==null){
            return pRootOfTree;
        }else {
            return left;
        }
    }

8、求树的深度

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度
思路：（1）可以采用递归，我觉得递归的时间应该是o(nlogn)？，因为需要遍历每个节点，然后找到一个节点的时间是logn

public int TreeDepth(TreeNode root) {
        if (root==null){
            return 0;
        }else {
            return Math.max(TreeDepth(root.left),TreeDepth(root.right))+1;
        }
    }

非递归：其实非递归的就是关键判断出遍历完每一层，也就是上面的一题，我们可以采用层次遍历+remain+nextCount的方式来遍历树,只需要在结束遍历一行的时候进行depth++来结算，这样每个节点只遍历一次，时间是o(n)

 /**
     * 非递归
     *
     * @param root
     * @return
     */
    public int TreeDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        ArrayDeque<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);
        int remain = 1, nextCount = 0;
        //起点是0
        int depth = 0;
        TreeNode node = null;
        while (!queue.isEmpty()) {
            node = queue.poll();
            //消耗当前一个
            remain--;
            if (node.left != null) {
                queue.offer(node.left);
                nextCount++;
            }
            if (node.right != null) {
                queue.offer(node.right);
                nextCount++;
            }
            //说明当前行遍历完毕
            if (remain == 0) {
                depth++;
                remain=nextCount;
                nextCount=0;
            }
        }
        return depth;
    }

2020.06.11

9、判断二叉树是否是平衡二叉树

输入一棵二叉树，判断该二叉树是否是平衡二叉树。

在这里，我们只需要考虑其平衡性，不需要考虑其是不是排序二叉树
思路：平衡二叉树就是每个节点的左右子树甚多差别不超过1
（1）获取左右孩子的深度，然后判断一下左右孩子的深度之差，如果大于1，则返回false
（2）递归函数，判断左右子树是否都满足此条件

 public boolean IsBalanced_Solution1(TreeNode root) {
        //1、空树，也是base case
        if (root == null) {
            return true;
        }
        int left = getDepth(root.left);
        int right = getDepth(root.right);
        //2、两种情况，需要当前满足平衡才能到子树去判断
        if (Math.abs((left - right)) > 1) {
            return false;
        }else {
            return IsBalanced_Solution1(root.left) && IsBalanced_Solution1(root.right);
        }
    }

    private int getDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }else {
            return Math.max(getDepth(root.left),getDepth(root.right));
        }
    }

9、找出二叉树中序遍历的下一个结点

给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。
思路：我们可以中序遍历一次，这样就可以找到所有的后继节点，但是这样的时间是o(n)，因为没有用到父指针。更好的思路是根据当前节点有没有右子树进行分类讨论（因为左根右，求后继根据右子树，求前驱根据左子树）。
（1）如果有右子树，因为根右，则右子树的最左节点就是当前节点（根）的后继
（2）如果没有右子树，因为左根，需要找到“根”，即找出哪个节点A的左孩子是当前节点（左），则节点A就是当前节点的后继。
具体见下面：

public TreeLinkNode GetNext(TreeLinkNode pNode) {
        if (pNode == null) {
            return null;
        }
        if (pNode.right != null) {
            //case1:有右孩子：需要找到右子树得最左节点
            TreeLinkNode cur = pNode.right;
            while (cur.left != null) {
                cur = cur.left;
            }
            return cur;
        }else {
            //case2：需要往上找到第一个作为左节点的父节点
            TreeLinkNode parent=pNode.next;
            while (parent!=null&&parent.left!=pNode){
                pNode=parent;
                parent=parent.next;
            }
            return parent;
        }
    }

扩展1:求二叉树中两个节点的最低公共祖先(二叉搜索树)

思路：写得很清楚，就是将当前节点root的值和需要寻找最近祖先的两个节点的值比较，如果root都大于两个，说明需要往小找，则递归到左子树；否则递归到右子树。
其他情况就是找到了最近祖先。

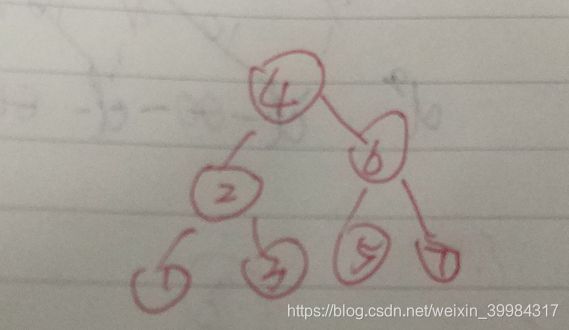
（1）传入的是两个叶子（1，3）–》2
（2）传入两个非叶子（2，6）–》4
（3）传入一个叶子和一个非叶子（2，3）–》2 （3，6）–》4

    /**
     * 在二叉搜索中中搜索
     *
     * @param node1
     * @param node2
     * @param root
     * @return
     */
    private static TreeNode findInBST(TreeNode node1, TreeNode node2, TreeNode root) {
        if (node1 == null || node2 == null || root == null) {
            return null;
        }
        if (root.val > node1.val && root.val > node2.val) {
            //case1
            return findInBST(node1, node2, root.left);
        } else if (root.val <node1.val && root.val <node2.val) {
            //case2
            return findInBST(node1,node2,root.right);
        }else {
            //case3:说明介于两者之间，则放前的root一定是最近的祖先
            return root;
        }
    }

扩展2:求二叉树中两个节点的最低公共祖先(有父指针的二叉树)

private static TreeLinkNode findParentLinkNode(TreeLinkNode node1, TreeLinkNode node2, TreeLinkNode root) {
    if (root == null || node1 == null || node2 == null) {
        return null;
    }
    TreeLinkNode cur1 = node1, cur2 = node2;
    int len1 = 0, len2 = 0;
    while (cur1 != root) {
        cur1 = cur1.next;
        len1++;
    }
    while (cur2 != root) {
        cur2 = cur2.next;
        len2++;
    }
    int dis = 0;
    //cur2指向长的
    if (len1 >= len2) {
        dis = len1 - len2;
        cur2 = node1;
        cur1 = node2;
    } else {
        dis = len2 - len1;
        cur2 = node2;
        cur1 = node1;
    }
    //长的先走
    while (dis > 0) {
        cur2 = cur2.next;
        dis--;
    }
    //然后一起走
    while (cur1 != cur2) {
        cur1 = cur1.next;
        cur2 = cur2.next;
    }
    return cur1;
}

10、判断二叉树是不是对称的

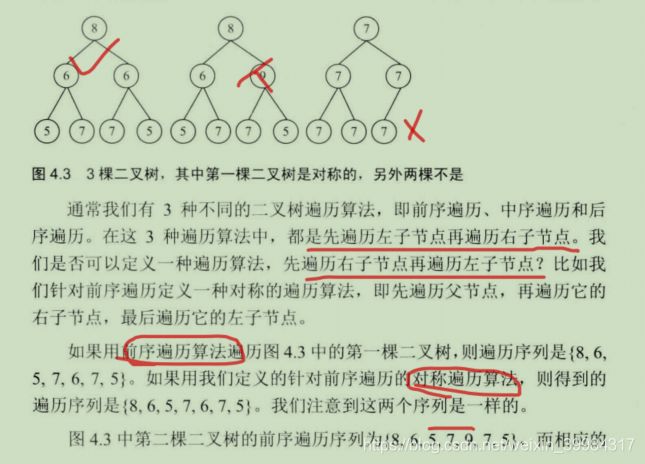
请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。
思路：设计前序遍历的对称算法，判断两个算法遍历序列是否完全一样。我们需要对比每个节点的左右孩子，如果左右孩子全部相等的话，也就是两棵树互为镜像，即使对称的意思。所以我们的算法就是需要对比根左右和根右左是否完全一样，

public class IsSymmetrical {

    boolean isSymmetrical(TreeNode pRoot) {
        if (pRoot == null) {
            return true;
        }
        //因为需要的两种不同的遍历策略，所以需要重新写一个函数
        return judge(pRoot, pRoot);
    }

    /**
     * 前序遍历算法和对称算法同时遍历
     * 注意递归的结束条件
     *
     * @param pRoot1
     * @param pRoot2
     * @return
     */
    private boolean judge(TreeNode pRoot1, TreeNode pRoot2) {
        //1、需要考虑是否为空
        if (pRoot1 == null && pRoot2 == null) {
            return true;
        }
        //这里也是需要考虑是否为空
        if (pRoot1 == null || pRoot2 == null) {
            return false;
        }
        //2、如果有一个不满足条件，直接false
        if (pRoot1.val != pRoot2.val) {
            return false;
        }
        //3、root1和root2刚好传入的左右呼唤：就是对称算法（相当于root1是左右、root2是右左）
        return judge(pRoot1.left, pRoot2.right) && judge(pRoot1.right, pRoot2.left);
    }
} 

11、请实现两个函数，分别用来序列化和反序列化二叉树

二叉树的序列化是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串，从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树遍历方式来进行修改，序列化的结果是一个字符串，序列化时通过 某种符号表示空节点（#），以 ！ 表示一个结点值的结束（value!）。
二叉树的反序列化是指：根据某种遍历顺序得到的序列化字符串结果str，重构二叉树。例如，我们可以把一个只有根节点为1的二叉树序列化为"1,"，然后通过自己的函数来解析回这个二叉树
思路：核心就是如何序列化就如何反序列化（递归）
（1） 序列化：如果root==null，则增加的是"#,"，说明空的节点使用#来填充；如果不为空，则追加节点的值和","；然后递归
（2）反序列化：使用下标index进行遍历字符串，需要判断当前字符串不为"#"才说明不是空，这个时候才开始new节点并且递归。
注意：序列化的时候最后确实会多一个逗号：1,2,4,#,#,5,#,#,3,6,#,#,7,#,#,同时最下层的空结点也会保存

public class SerializeAndDeserialize {
    String Serialize(TreeNode root) {
        StringBuilder sb = new StringBuilder();
        //1、说明是空，使用#区分
        if (root == null) {
            sb.append("#,");
        } else {//2、需要使用，分割节点，区分22和2 2
            sb.append(root.val).append(",");
            //3、开始递归加入子树
            sb.append(Serialize(root.left));
            sb.append(Serialize(root.right));
        }
        return sb.toString();

    }

    /**
     * 注意index的起点，且不能将index放入递归中(关键)
     */
    int index = -1;

    TreeNode Deserialize(String str) {
        if (str==null||str.length()==0){
            return null;
        }
        //调用一次递归则处理后一个
        index++;
        String[] strings = str.split(",");
        TreeNode res = null;
        //base case
        if (strings[index].equals("#")) {
            return null;
        } else {
            //不是空结点才递归
            res = new TreeNode(Integer.valueOf(strings[index]));
            res.left = Deserialize(str);
            res.right = Deserialize(str);
        }
        return res;
    }

}

前序序列化的效果会比较好，不需要全部都取出来来才能构建树

12、二叉搜索树，请找出第k小的结点

给定一棵二叉搜索树，请找出其中的第k小的结点。例如， （5，3，7，2，4，6，8） 中，按结点数值大小顺序第三小结点的值为4。
思路：就是中序遍历，然后找到中序便利的第k个节点。

public class FindKthNode {

    TreeNode KthNode(TreeNode pRoot, int k) {
        if (pRoot == null || k <= 0) {
            return null;
        }
        ArrayList<TreeNode> inorder = inorder(pRoot);
        //需要处理k过大
        if (k>inorder.size()){
            return null;
        }
        return inorder.get(k-1);
    }

    /**
     * 二叉树的中序遍历
     * @param pRoot
     * @return
     */
    private ArrayList<TreeNode> inorder(TreeNode pRoot) {
        ArrayList<TreeNode> res=new ArrayList<>();
        if (pRoot==null){
            return res;
        }
        ArrayDeque<TreeNode> stack=new ArrayDeque<>();
        TreeNode cur=pRoot;
        while (cur!=null||!stack.isEmpty()){
            //如果cur不为空则往左边走，一直走到最左边
            if (cur!=null){
                stack.push(cur);
                cur=cur.left;
            }else {
                //如果cur为空，则出栈结算，往右边走
                cur=stack.pop();
                res.add(cur);
                cur=cur.right;
            }
        }
        return res;
    }

}