全文共3179字,推荐阅读时间10~15分钟。
文章共分四个部分:
-
作业分析
-
评测相关
-
重构策略
-
初体验感受
作业分析
第一次作业
第一次作业要求我们实现一个简单的幂函数求导工具,没有乘积和复合的情况。
UML图如下

- 代码结构
第一次作业的代码结构并不复杂,从主类调用Poly构造多项式,然后在Term中建项。没有涉及到继承和多态,结构和逻辑都比较清晰。
- 思路解析
-
主类中调用
Poly进行构造,在构造的同时进行合法性检查。(由于保证输入正确,所以并没有影响。) -
由于第一次作业只涉及简单的加减连接,所以可以直接使用
split()函数进行拆解后建项。 -
求导按照公式进行即可,最后把结果存在一个多项式中输出。
- 复杂度分析
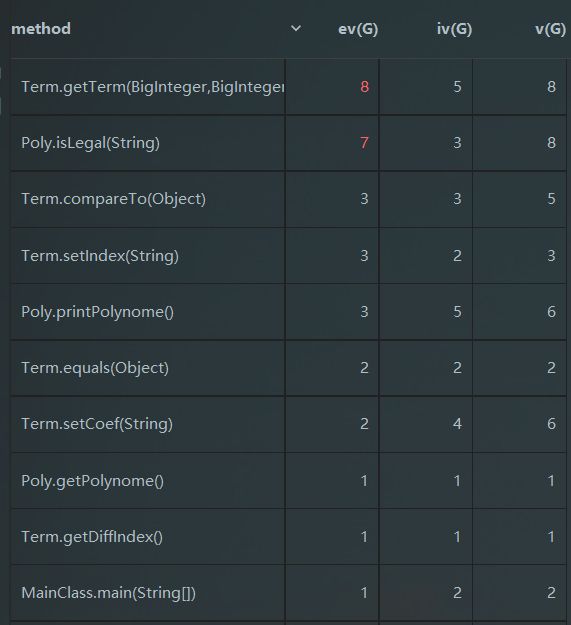
从反馈结果可以看出,由于把合法性判断和构造融合在一起,造成了isLegal()方法和getTerm()方法的复杂度过高。在第一次作业中,其实这两个功能并非紧耦合,完全可以拆开分别实现。在其他方法中,还是比较好的体现了“高内聚低耦合”的设计思想,均没有较高的复杂度。
第二次作业
第一次作业要求我们实现一个的幂函数、三角函数混合的求导工具,出现了乘积的情况。
UML图如下
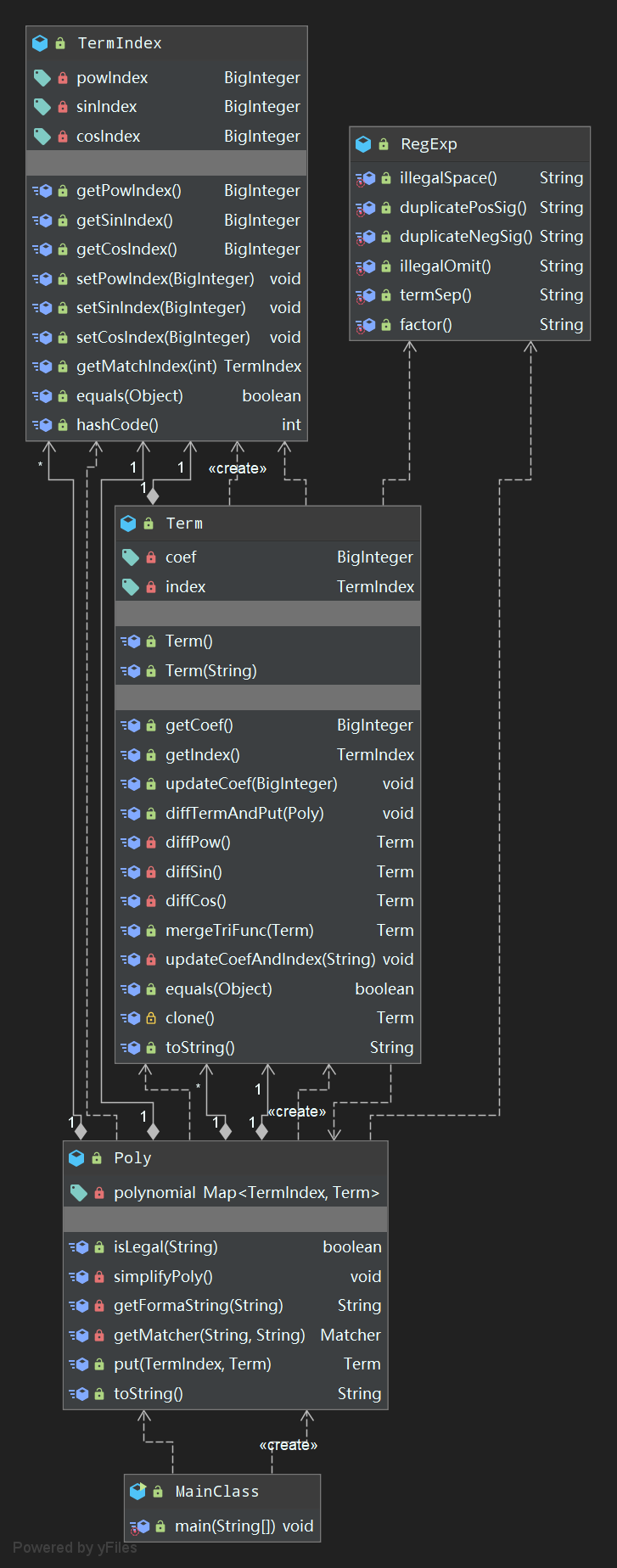
- 代码结构
代码架构基本延续了第一次的设计风格,新增了RegExp的自定义工具类以及\(ax^bsin^c(x)cos^d(x)\)的指数存储类。
- 思路解析
-
基本思路和第一次相同,但是新增使用正则表达式判断非法格式的功能。
-
对于每一个分割出来的项,先化简为前文提到的标准格式,之后再进行求导操作。
-
化简时构造了一个“循环熔断”,根据某一项的系数和指数的大小,构造出可以合并的两种可能项,但后在
Poly中进行查找。这样的构造循环执行5次基本可以实现所有能够利用\(sin^2(x)+cos^2(x)=1\)合并的情况。(5~6次是10000组测试用例的实验结果,可以称为经验结论。)
- 复杂度分析
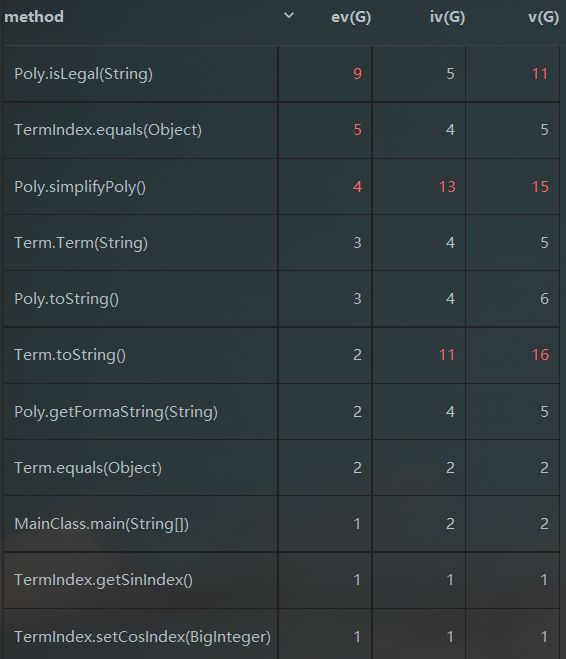
从反馈结果可以看出,相比于第一次作业中判断非法和构造项的紧耦合情况,在单独提取出判断部分后,Term的构造方法复杂度直线下降。但是由于isLegal()部分没有做优化,导致复杂度相比于第一次有所上升。现在回看起来,isLegal()的复杂度完全可以通过异常来判断。只要保证每一层的预处理正确,进入下一层后,出现不能解析的情况就一定是WRONG FORMAT.(但是这种方法的逻辑复杂度很高,需要编程人员提前考虑到所有的特殊情况,避免误判。)
第三次作业
第三次作业要求我们实现一个含有幂函数、三角函数,并且支持多层嵌套的求导工具。
UML图如下

- 代码结构
由于第三次作业使用了递归的思路来进行链式求导操作,导致了第三次作业的代码结构和前两次完全不同,并且引入了继承和多态。但是基本的逻辑框架没有变,依然是Poly->Term->Factor的解析层次,只是出现了例如Factor->Poly的逆构造情况。
- 思路解析
-
将格式错误交给异常处理
-
使用多态来实现链式求导
-
输出时依然采用递归的思路,层层求导,层层返回。
- 复杂度分析
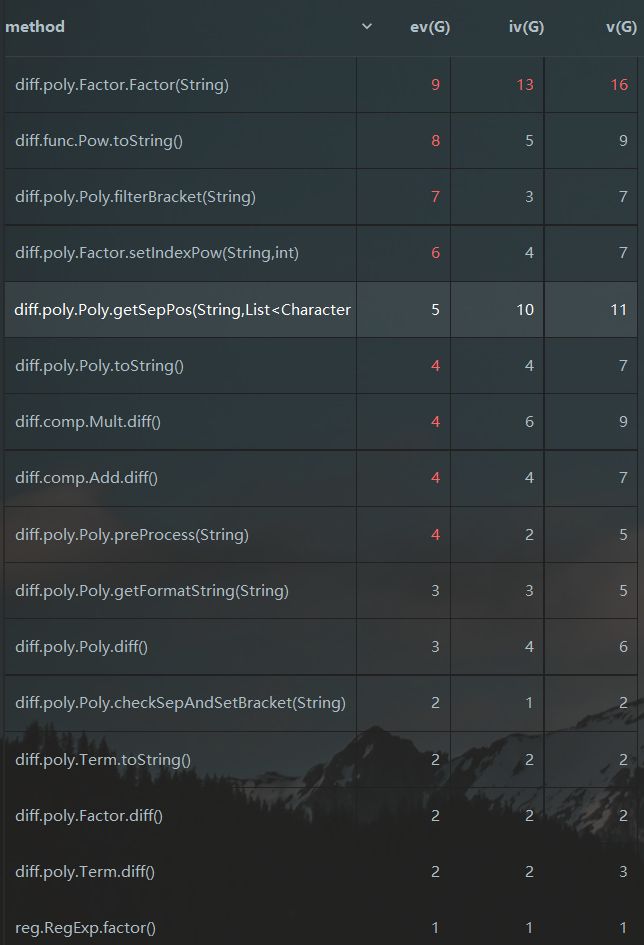
从反馈结果可以看到,前两次作业复杂度最高的部分都出现在格式判断上,但因为改变了WRONG FORMAT的判断方式,这一次没有再出现了。但是构造方法却出现了比较高的复杂度——我想原因就出现在逆向构造上。由于逆向构造代码流程的复杂性,其实可以引入工厂模式,将每个构造(包括正向和负向)都有传入的参数来决定,这样可以封装对象的创建逻辑,降低复杂度。
评测相关
自己的bug
第一次作业
在第一次作业中,由于将求导公式:
- \((Cx^n)'=Cnx^{n-1}\)
- \((C)'=0\)
误认为前者在\(n=0\)时和后者是完全等价关系,造成存求导结果时指数为-1和0的项的混合,导致了系数计算错误。粗略地看会认为是数学问题,但其实是对Java容器的equals()方法不熟悉,在放置时应该考虑到原项和求导结果的分离。
第二次作业
在第二次作业中,由于对正则的理解存在误区:
str.replaceAll("++|+++","+");
对于存在相互包含关系的正则,在匹配时和顺序没有关系,而是采用最优匹配原则。这就直接导致了在出现以下类型的式子时:
\(+++x\)
会得到:
\(++x\)
而不是:
\(x\)
因为我并没有采用大正则直接提取项的方式,所以在预处理中就会出现很多难以预料的情况。(其中大多数都是特殊数据的问题)这也是一种常见的“各有损益”的情况,大正则有较高的代码复杂度,但是预处理就对逻辑判断提出了更高的要求,所以OO教我的这一堂“取舍”课,算是很深刻了。
第三次作业
第三次作业中,由于使用了递归思想进行多项式的拆解,所以解析每一层时,符号的省略问题就是重点。在递归时,我少考虑了Factor->Poly的逆向构造情况,在解决\(-(-(x-x))\)时就会造成第二层减号被错误解析。
在反思的过程中,我发现导致这个错误的原因主要在于:我在重写toString()方法时,都是只保证了在debug模式时的预览框中自己能够看懂即可,无意地丢掉了很多有用信息,也正是因为丢掉了-号才导致我不能够找到递归层次的缺失。
Hack所用的策略
主要有两种方式:
- 使用完成作业时有意义的样例进行测试
- 利用评测机自己生成数据
三次作业中,发现的Bug基本都出现在优化部分,具有代表性的几种可以列举如下
- 对
1的省略忽视了123等以1开头的数据,造成结果为23. -1)不能随意省略,因为-1可能作为指数而不是系数。- \((-(-(x-x)))\)等多层嵌套的情况会因为没有优化而一味递归造成
memory error。
评测机简要介绍
这是评测机的working directory
-
center:存放评测的核心控制代码,用于组织编译->运行->反馈功能 -
data:存放自动生成的数据 -
download_data:存放测试中出现问题的数据,可以用于回归测试。 -
factory:存放数据生成代码 -
output:存放各个测试代码的输出 -
result:存放各个测试代码的结果 -
ruler:存放标程 -
src:存放源码 -
filter.py:用于格式化数据以提交
在一开始开发评测机时,由于浮点运算对性能的高要求,就考虑过适配服务器端的评测机,所以并没有采用.bat批处理文件。最后选择了单纯地使用python进行编译->运行->验证->反馈的评测过程,同时使用ssh和服务器端进行交互。(之后在CentOS/Ubuntu上实测可以进行作业处理)
在整个第一单元的学习过程中,除了OO作业教会我的迭代思想之外,根据需求不停优化评测机对我自己的OOP工程能力其实也是一个不可忽视的方面,甚至还能同时学习python的OO模式。
考虑到评测机的迭代问题,我把验证逻辑单独封装在一个包中,每一次更新只需要根据作业的数据要求修改修改验证逻辑中的数据生成单元即可。
我最开始开发评测机时主要是为了测试自己的问题,之后因为互测的存在才想着增加评测机的回归测试、对比测试等功能,随着OO课程的学习,预感还会有更多的花样能被加进我的小小评测机里。
重构策略
在三次作业的完成过程中,我都是先确定好架构再开始完成的,所以没有遇到需要从头开始重构的情况。
但是值得一提的是,出于扩展性,本来是想要在第二次作业就实现链式求导的,奈何链式求导化简复杂度相比于基本形式的化简高了许多,因此最后没有采用链式求导来完成第二次作业,如果选择了可能就会重构了吧。
初体验感受
总的来说,OO的初体验还算开心和满足,每一周我都能问心无愧地说尽了自己的最大努力,每一次都想要做到自己能够到达的最好程度,尽管每次都会不多不少有一个事后看起来无比明显的Bug。
如果说前两次的Bug让我积累到了学术上的、技术上的经验,让我对Java语言本身和评测机开发都有了不一样的理解之外。那么第三次的Bug是在教我一些人生路上的道理。
为什么这么说呢?在完成作业后,我会和朋友们一起讨论优化,然后就提到了一种-的处理方式,听懂了后我觉得很有道理,就直接改了提交了。因为修改部分逻辑也不复杂,所以我自认为不会影响正确性,因此之后朋友提出让我帮忙用评测机测试时,我也就毫不犹豫地答应了。之后一直到周六的截止日期前,我都在帮忙找Bug.
可是谁能料到?周日我下载下来互测room中其他同学的代码后,和自己的代码一起测试,一测,就出问题了……
这能怪谁呢,忙是我自己答应要帮的,提交按钮也是我自己按的。无比明显的键盘失误就摆在我眼前,但是已经没有办法改变了。
到最后公布结果,看到这个Bug给我带来的损失很大,但是我却一下子释然了——这就是人生路上总会遇到的境况,谁都有为了别人忘记自己的时候,这种行为从来没有好坏和对错,日子过得心安和快乐才是最重要的,何况更重要的是,我自己的评测机能把自己的问题给找出来,这才是最大的收获啊!
一周前的我也很难想象,OO居然能给我上这样一堂和课程内容本身没有什么关联的课。
谢谢讨论区里的老师、助教、同学,是大家让我真正领会了一句很久以前看见的话:
一个人可以走得很快,但一群人才能走得更远。