遗传算法与深度学习实战（6）——DEAP框架初体验

0. 前言

我们已经了解了 DEAP 库中的重要数据结构和工具，为了快速掌握 DEAP，本节中，我们将介绍 DEAP 框架下的遗传算法构建流程，并使用 DEAP 解决简单的 OneMax 问题。

1. OneMax 问题介绍

OneMax 问题是一个简单的优化任务，通常作为遗传算法 Hello World。OneMax 任务是查找给定长度的二进制串，最大化该二进制串中数字的总和。例如，对于长度为 5 的 OneMax 问题，10010 的数字总和为 2，01110 的数字总和为 3。
显然，此问题的最优解为每位数字均为 1 的二进制串。但是对于遗传算法而言，其并不具备此知识，因此需要使用其遗传算子寻找最优解。算法的目标是在合理的时间内找到最优解，或者至少找到一个近似最优解。

2. 遗传算法要素定义

在进行实践前，应首先明确遗传算法中所用到的要素定义。

1. 选择染色体：由于 OneMax 问题涉及二进制串，因此每个个体的染色体直接利用代表候选解的二进制串表示是一个自然的选择。在 Python 中，将其实现为仅包含 0/1 整数值的列表。染色体的长度与 OneMax 问题的规模匹配。例如，对于规模为 5 的 OneMax 问题，个体 10010 由列表 [1,0,0,1,0] 表示。
2. 计算适应度：由于要最大化该二进制串中数字的总和，同时由于每个个体都由 0/1 整数值列表表示，因此适合度可以设计为列表中元素的总和，例如：sum([1,0,0,1,0])= 2。
3. 选择遗传算子：选择遗传算子并没有统一的标准，通常可以尝试几种选择方案，找到最适合的方案。其中选择算子通常可以处理任何染色体类型，但是交叉和突变算子通常需要匹配使用的染色体类型，否则可能会产生无效的染色体。
   • 选择算子：本节选用锦标赛选择
   • 交叉算子：本节选用单点交叉
   • 突变算子：本节选用位翻转突变
4. 设定停止条件：限制繁衍的世代数通常是一个不错的停止条件，它可以确保算法不会永远运行。另外，由于我们知道了 OneMax 问题的最佳解决方案(一个全为 1 的二进制串，也就是说其适应度等于代表个体的列表长度)，因此可以将其用作另一个停止条件。需要注意的是，对于现实世界中的多数问题而言，通常不存在这种可以公式化精确定义的先验知识。

3. 使用 DEAP 解决 OneMax 问题

接下来，我们使用 DEAP 构建一个解决 OneMax` 问题的求解器。

3.1 遗传算法要素配置

在开始实际的遗传算法流程之前，需要根据上述要素的设计利用代码实现。

(1) 首先导入所用库：

from deap import base
from deap import creator
from deap import tools
import random
import matplotlib.pyplot as plt

(2) 声明常量用于设置 OneMax 问题的参数并控制遗传算法的行为：

#超参数声明
ONE_MAX_LENGTH = 100    #length of bit string to be optimized
POPULATION_SIZE = 200   #number of individuals in population
P_CROSSOVER = 0.9       #probability for crossover
P_MUTATION = 0.1        #probability for mutating an individual
MAX_GENERATION = 50     #max number of generations for stopping condition

(3) 使用 Toolbox 类创建 zeroOrOne 操作，该操作用于自定义 random.randomint(a,b) 函数。通过将参数 a 和 b 固定为值 0 和 1，当在调用此运算时时，zeroOrOne 运算符将随机返回 0 或 1：

toolbox = base.Toolbox()#定义toolbox变量
toolbox.register("zeroOrOne", random.randint, 0, 1)#注册zeroOrOne运算

(4) 需要创建 Fitness 类。由于这里只有一个目标——最大化数字总和，因此选择 FitnessMax 策略，使用具有单个正权重的权重元组：

creator.create("FitnessMax", base.Fitness, weights=(1.0,))

(5) 在 DEAP 中，通常使用 Individual 的类来代表种群中的每个个体。使用 creator 工具创建该类，使用列表作为基类，用于表示个体的染色体。并为该类增加 Fitness 属性，该属性初始化为定义的 FitnessMax 类：

creator.create("Individual", list, fitness=creator.FitnessMax)

(6) 接下来，注册 individualCreator 操作，该操作创建 Individual 类的实例，并利用自定义 zeroOrOne 操作随机填充 0/1。注册 individualCreator 操作使用基类 initRepeat 操作，并使用以下参数对基类进行实例化：

• 将 creator.Individual 类作为放置结果对象的容器类型
• zeroOrOne 操作是生成对象的函数
• 常量 ONE_MAX_LENGTH 作为要生成的对象数目

由于 zeroOrOne 运算符生成的对象是 0/1 的随机数，因此，所得的 individualCreator 运算符将使用 100 个随机生成的 0 或 1 填充单个实例：

toolbox.register("individualCreator", tools.initRepeat, creator.Individual, toolbox.zeroOrOne, ONE_MAX_LENGTH)

(7) 最后，注册用于创建个体列表的 populationCreator 操作。该定义使用带有以下参数的 initRepeat 基类操作：

• 将列表类作为容器类型
• 用于生成列表中对象的函数—— personalCreator 运算符

这里没有传入 initRepeat 的最后一个参数——要生成的对象数量。这意味着，当使用 populationCreator 操作时，需要指定此参数用于确定创建的个体数：

toolbox.register("populationCreator", tools.initRepeat, list, toolbox.individualCreator)

(8) 为了简化适应度(在 DEAP 中称为 evaluation )的计算，首先定义一个独立的函数，该函数接受 Individual 类的实例并返回其适应度。这里定义 oneMaxFitness 函数，用于计算个体中 1 的数量：

def oneMaxFitness(individual):
    return sum(individual), # deap中的适用度表示为元组，因此，当返回单个值时，需要用逗号将其声明为元组。

(9) 接下来，将 evaluate 运算符定义为 oneMaxfitness() 函数的别名。使用 evaluate 别名来计算适应度是 DEAP 的一种约定：

toolbox.register("evaluate", oneMaxFitness)

(10) 遗传算子通常是通过对 tools 模块中的现有函数进行别名命名，并根据需要设置参数值来创建的。根据上一小节设计的要素创建遗传算子：

toolbox.register("select", tools.selTournament,tournsize=3)
toolbox.register("mate", tools.cxOnePoint)
# mutFlipBit函数遍历个体的所有特征，并且对于每个特征值，
# 都将使用indpb参数值作为翻转（应用not运算符）该特征值的概率。
# 该值与突变概率无关，后者由P_MUTATION常数设置。
# 突变概率用于确定是否为种群中的给定个体调用mutFlipBit函数
toolbox.register("mutate", tools.mutFlipBit, indpb=1.0/ONE_MAX_LENGTH)

3.2 遗传算法解的进化

接下来，实现遗传流程，优化 OneMax 问题的解。

(1) 通过使用之前定义的 populationCreator 操作创建初始种群，并以 POPULATION_SIZE 常量作为该操作的参数，并初始化 generationCounter 变量，用于判断世代数：

population = toolbox.populationCreator(n=POPULATION_SIZE)
generationCounter = 0

(2) 为了计算初始种群中每个个体的适应度，使用 map() 函数将 evaluate 操作应用于种群中的每个个体。由于 evaluate 操作是 oneMaxFitness() 函数的别名，因此，迭代的结果由每个个体的计算出的适应度元组组成。 得到结果后将其转换为元组列表：

fitnessValues = list(map(toolbox.evaluate, population)

(3) 由于 fitnessValues 的项分别与 population (个体列表)中的项匹配，因此可以使用 zip() 函数将它们组合并为每个个体分配相应的适应度元组：

for individual,fitnessValue in zip(population, fitnessValues):
	individual.fitness.values = fitnessValue

(4) 由于适应度元组仅有一个值，因此从每个个体的适应度中提取第一个值以获取统计数据：

fitnessValues = [indivalual.fitness.values[0] for individual in population]

(5) 统计种群每一代的最大适应度和平均适应度。创建两个列表用于存储统计值：

maxFitnessValues = []
meanFitnessValues = []

(6) 遗传流程的主要准备工作已经完成，在循环时还需设置停止条件，通过限制世代数来设置一个停止条件，而通过检测是否达到了最佳解(所有二进制串位都为 1 )作为另一个停止条件：

while max(fitnessValues) < ONE_MAX_LENGTH and generationCounter < MAX_GENERATIONS:

(7) 更新世代计数器：

	generationCounter = generationCounter + 1

(8) 遗传算法的核心是遗传运算符。第一个是 selection 运算符，使用先前利用 toolbox.select 定义的锦标赛选择。由于我们已经在定义运算符时设置了锦标赛大小，因此只需要将物种及其长度作为参数传递给选择运算符：

	offspring = toolbox.select(population, len(population))

(9) 被选择的个体被赋值给 offspring 变量，接下来将其克隆，以便我们可以应用遗传算子而不影响原始种群。需要注意的是尽管命名为 offspring，但它们仍然是前一代的个体的克隆，我们仍然需要使用 crossover 运算符将它们配对以创建实际的后代：

	offspring = list(map(toolbox.clone, offspring)

(10) 下一个遗传算子是交叉。已经在上一小节中定义为 toolbox.mate 运算符，并且其仅仅是单点交叉的别名。使用 Python 切片将 offspring 列表中的每个偶数索引项与奇数索引项对作为双亲。然后，以 P_CROSSOVER 常数设置的交叉概率进行交叉。这将决定这对个体是会交叉或保持不变。最后，删除后代的适应度值，因为它们现有的适应度已经不再有效：

	for child1,child2 in zip(offspring[::2],offspring[1::2]):
		if random.random() < P_CROSSOVER:
			toolbox.mate(child1,child2)
			del child1.fitness.values
			del child2.fitness.values

(11) 最后一个遗传运算符是变异，先前已注册为 toolbox.mutate 运算符，并设置为翻转位突变操作。遍历所有后代项，将以由突变概率常数 P_MUTATION 设置的概率应用变异算子。如果个体发生突变，我们确保删除其适应性值。由于该值可能继承自上一代，并且在突变后不再正确，需要重新计算：

	for mutant in offspring:
		if random.random() < P_MUTATION:
			toolbox.mutate(mutant)
			del mutant.fitness.values

(12) 没有交叉或变异的个体保持不变，因此，它们的现有适应度值(已在上一代中计算出)就无需再次计算。其余个体的适应度值为空。使用 Fitness 类的 valid 属性查找这些新个体，然后以与原始适应性值计算相同的方式为其计算新适应性：

	freshIndividuals = [ind for ind in offspring if not ind.fitness.valid]
	freshFitnessValues = list(map(toolbox.evaluate,freshIndividuals))
	for individual,fitnessValue in zip(freshIndividuals,freshFitnessValues):
		individual.fitness.values = fitnessValue

(13) 遗传算子全部完成后，就可以使用新的种群取代旧的种群了：

	population[:] = offspring

(14) 在继续下一轮循环之前，将使用与上述相同的方法统计当前的适应度值以更新统计信息：

	fitnessValues = [ind.fitness.values[0] for ind in population]

(15) 获得最大和平均适应度值，将它们的值添加到统计列表中：

	maxFitness = max(fitnessValues)
	meanFitness = sum(fitnessValues) / len(population)
	maxFitnessValues.append(maxFItness)
	meanFItnessValues.append(meanFItness)
	print(“- Generation {}: Max Fitness = {}, Avg Fitness = {}”.format(generationCounter,
	maxFitness, meanFitness)

(16) 此外，使用得到的最大适应度值来找到最佳个体的索引，并打印出该个体：

	best_index = fitnessValues.index(max(fitnessValues))
	print(“Best Individual = “, *population[best_index], “\n”)

(17) 满足停止条件并且遗传算法流程结束后，可以使用获取的统计信息，使用 matplotlib 库可视化算法执行过程中的统计信息，展示各代个体的最佳和平均适应度值的变化：

plt.plot(maxFitnessValues,color=’red’)
plt.plot(meanFitnessValues,color=’green’)
plt.xlabel(‘Generation’)
plt.ylabel(‘Max / Average Fitness’)
plt.title(‘Max and Average fitness over Generation’)
plt.show()

3.3 运行结果

运行程序时，可以看到程序运行输出：

- Generation 27: Max Fitness = 99.0, Avg Fitness = 96.805
Best Indivadual =  1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 

- Generation 28: Max Fitness = 99.0, Avg Fitness = 97.235
Best Indivadual =  1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 

- Generation 29: Max Fitness = 99.0, Avg Fitness = 97.625
Best Indivadual =  1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 

- Generation 30: Max Fitness = 100.0, Avg Fitness = 98.1
Best Indivadual =  1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 

可以看到 30 代后算法找到全1解，结果适应度为 100，并停止了遗传流程。平均适应度开始时仅为 53 左右，结束时接近 100：

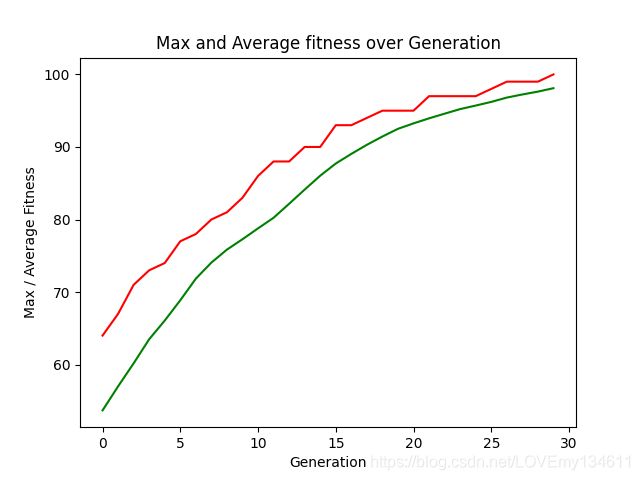
该图说明了最大适应度与平均适应度是如何随着世代数的增加而逐步增加。

3.4 eaSimple 函数

除了从头开始实现进化过程外，我们也可以使用 DEAP 内置的 eaSimple 函数执行进化过程。

(1) 首先，使用 toolbox 创建种群。接下来，创建一个 HallOfFame 对象，用来追踪表现优异的个体。在本节中，我们只追踪最佳个体，由于个体是 NumPy 数组，我们需要编写排序算法对个体适应度排序：

population = toolbox.populationCreator(n=POPULATION_SIZE)
hof = tools.HallOfFame(1, similar=numpy.array_equal)

(2) 创建一个 Statistics 对象 stat，使用它来跟踪种群适应度的变化。使用 register 函数添加描述性统计信息，传入相应的 NumPy 函数来评估统计信息：

stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", numpy.mean)
stats.register("std", numpy.std)
stats.register("min", numpy.min)
stats.register("max", numpy.max)

(3) eaSimple 函数的输入参数包括 pop、toolbox、halloffame 和 stats 对象，以及设置交叉率 (cxpb)、突变率 (mutpb) 和迭代代数 (ngen) 的超参数：

algorithms.eaSimple(pop, toolbox, cxpb=P_CROSSOVER, mutpb=P_MUTATION, ngen=MAX_GENERATION, stats=stats,
                    halloffame=hof,verbose=None)

小结

OneMax 问题是遗传算法和进化计算领域中的一个简单但经典的问题，常用于展示如何应用进化算法进行优化任务。在本节中，我们介绍了 DEAP 框架下遗传算法构建的通用流程，并使用 DEAP 解决简单的 OneMax 问题。

系列链接

遗传算法与深度学习实战（1）——进化深度学习
遗传算法与深度学习实战（2）——生命模拟及其应用
遗传算法与深度学习实战（3）——生命模拟与进化论
遗传算法与深度学习实战（4）——遗传算法详解与实现
遗传算法与深度学习实战（5）——遗传算法框架DEAP