一.综述
第一单元的主题为多项式求导,给定多项式函数,输出其导函数。其中第一次作业仅限幂函数,第二次作业添加了三角函数,第三次作业添加了函数之间的嵌套,相比人人皆知的求导规则,又臭又长,每次都不尽相同的格式要求或许才是真正磨人的地方。
二.作业与BUG分析
第一次作业
1.代码思路
第一次作业总体思路是先用正则拆项,然后根据拆得字符串提取系数与指数构造每一项,再将求导后的每一项添加进一个新多项式中。先根据指数排序,再合并同类项,将正数提到首项,最后输出。
2.代码度量分析
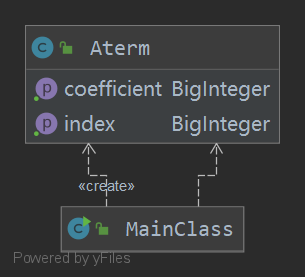
UML类图
第一次作业可谓是憨憨操作,只有一个类,还将大量内容放置在了主类中,尽管根据不同的功能分了不同的函数,层次结构较为清楚,但是可拓展性和面向对象的特性都是渣渣,不过考虑到这时的我连JAVA都不会怎么会用,暂且还能忍。、
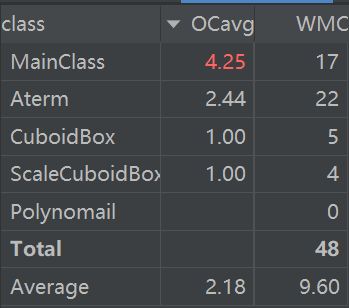
复杂度
可以看出主类复杂度较高,这与在其中添加了大量排序、合并等循环有关,出现憨憨立方体是因为继承自寒假作业。
3.bug分析
第一次作业较简单,在调试完毕后一次提交即通过了整次作业所有测试点。
第二次作业
1.代码思路
第二次作业是在第一次作业期基础上的改动,输入方面将正则表达式与读取部分进行改动,输出方面对应调整。对于单项式,在原有的基础上添加sin与cos的系数两项,由于计算通式较为复杂,因此选择了采用求导乘法公式,不过因此写了大量的多项式加法与乘法,而其中绝大多数都在第三次作业中重构,有些得不偿失。
2.代码度量分析
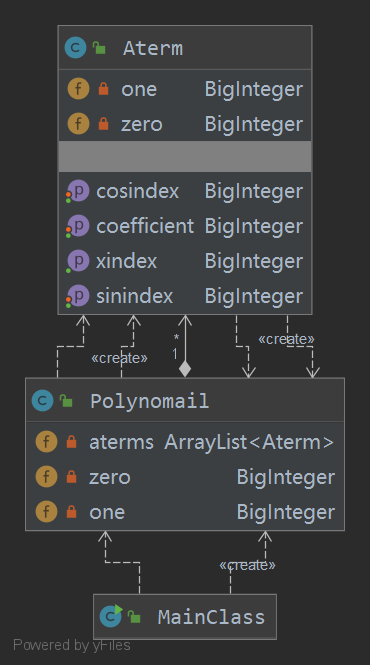
UML类图
第二次作业终于分别构造了多项式与单项式类,并且给添加了大量的多项式与项之间的乘法与加法运算,但是遗憾的是由于可拓展性太弱,多数内容在第三次作业中并没有用上,第三次作业的多项式类与单项式类几乎完全重构。
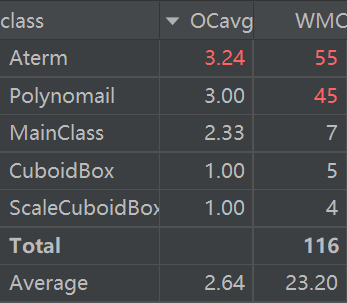
复杂度
可以看出被寄予厚望的单项式与多项式复杂度依然较高,这与其中大量功能(例如字符串与项之间的转换,求导)都集成在一个方法中有关。
Aterm类中复杂度最高的几个方法几乎全部与字符串处理相关(空间所限不贴图了)。
由于继承自第一次作业,因此根本用不到的憨憨立方体依然出现。
3.bug分析
第二次从作业开始,虽然通过了弱测与中测,但是在强测与互测中一共发现了三个bug,其中两个是对指导书的要求不够明确导致的。
- 不清楚是否会出现非法空白符,因此替换了所有空白符导致在遇到垂直制表符时没有输出WF而是正常运算。
- 对于指数不能超过10000误解,导致没有在输入时检测指数而是在化简后对每一项进行检测,因此对于每一项指数都不大于10000但是相乘后指数大于10000的所有数据都会错报WF。
- 在根据输入字符串构造每一项的时候,我在检测到字符串头负号是将默认系数设为-1,否则设为+1,看似没有问题,但是如果首项为-1,则会在系数为-1的基础上,再与检索到的-1相乘,导致由负转正。而后的我自作聪明,在检索到数字相乘的时候将数字全部变为绝对值,直接导致所有在项首之外出现的负数都当成了正数来算。
三个bug中两个都十分低级,都是由于没有足够仔细研究说明导致的。这两个bug本该可以在我发现疑问后及时弄清楚问题而避免,但是却因为自己的自作聪明而白白失分。
第三次作业
1.代码思路
第三次作业是第二次作业的基础上的魔改,单项式由四元组改为储存因子的ArrayList,而因子又可分为幂函数、三角函数、表达式(多项式)加括号,幂函数的求导部分沿用了前面的作业,三角函数部分则额外添加。通过多次递归、化整为零,再复杂的表达式也不怕,然而由于在输入输出,数据储存等方面难度与前两次作业的巨大差别,以及前两次作业的可拓展性太差,导致多项式与单项式部分几乎全部重构,不仅引入了新的bug,还花费了大量时间。
2.代码度量分析
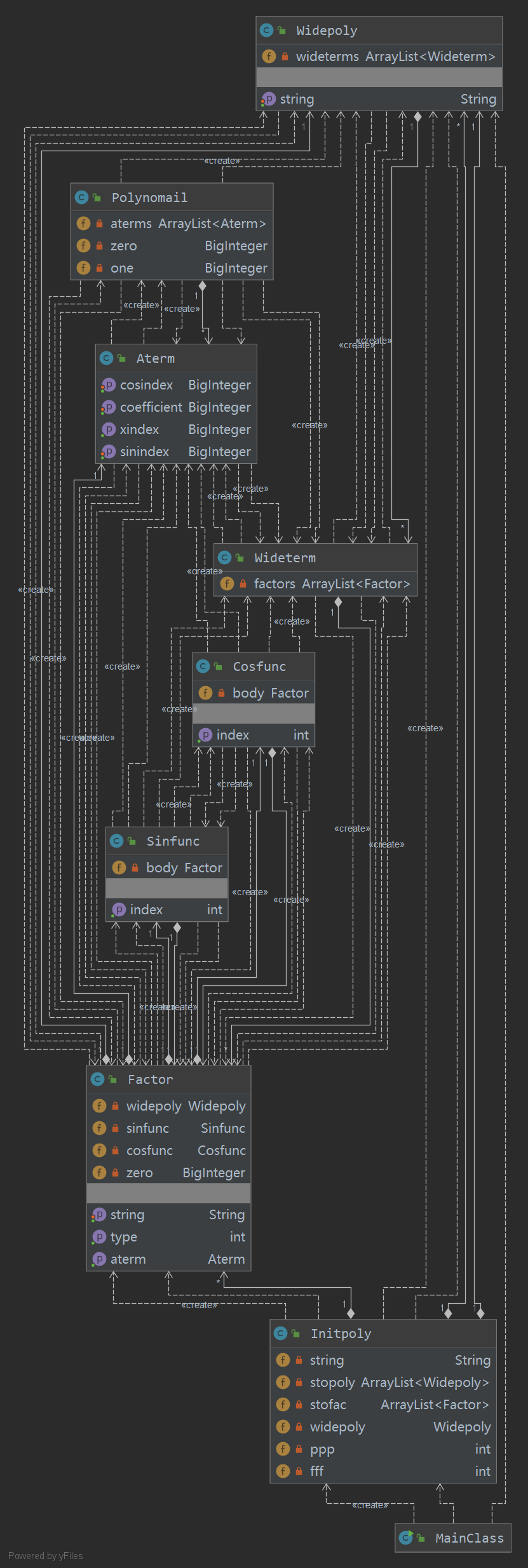
UML类图
可以看出由于问题难度的提升,出现了大量不同类间的相互调用,使得复杂度急剧上升。
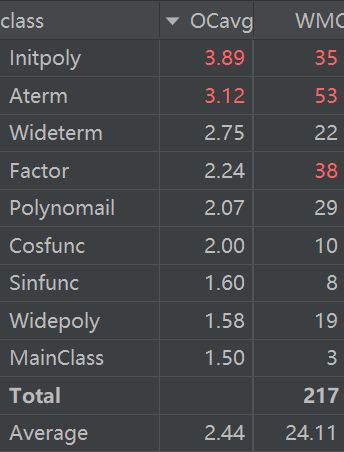
复杂度
对于起连接作用的多项式与单项式类,复杂度并未太高,复杂度较高的一个是从作业二中继承来的幂函数(其实尽管三角函数部分用不到,但是并未删去)Aterm类,另则一个是相当程度上承担了main函数功能的initpoly类,用于进行格式检查,递归去括号,代码预处理等功能,因为其经常与字符串打交道,因此复杂度也居高不下。
3.bug分析
第三次作业由于初期思维不是很清晰再加上时间紧张,出现了较多bug,其中多数出现在格式处理。
- 在正则表达式中添加合法空白项时忘了项首空白项导致无法匹配开头空格导致错误输出WF。
- 在输出时由于完全复用了上次的代码,导致x**2被错误化简为了x*x,输出格式错误。
- 上次为了简便而将系数为0的项输出为空,没有删除,而此次对于每一项的处理又复用了上一次的代码,导致此次在处理sin(0)时,0不输出,而括号内为空导致无法处理。
- 对于新构造的三角函数,括号内因子直接使用“=”与旧的三角函数因子进行赋值,这就造成因子相同的三角函数共用一个因子(地址相同)。而在输出时判断因子为0后直接将因子清空,然后检测到因子为空就输出一个空串,但是在前面整理因子时默认添加一个1作为系数,直接导致清空后的因子在下一次输出时变为了1。
三.分析发现他人bug的策略
第一二次作业只是简单的跟着感觉构造一些较为复杂的表达式,效果很差。
第三次作业开始,我在写程序的时候根据自己的对易错点的理解与编程中实际出现的问题,加上自己认为一些比较难以处理的数据,全都记录下来,留待互测阶段使用,同时也自己构造了一些较为难以处理的数据,总体hack成功率在20%到40%左右,较为有效。
四.应用对象创建模式来重构
从第一次作业开始,就可以构造多项式与单项式类及其对应的正则表达式,为了方便,单项式类可以使用简单的系数、指数两个数字储存,求导与输入输出均可对应实现。
第二次作业在输入方面将正则表达式与读取部分进行改动,输出方面对应调整即可。由于因子变多,可以考虑每一项使用ArrayList存储因子,增加三角函数因子类,增加多项式求导乘法法则。
第三次作业,增加表达式因子类,增加链式法则,三角函数因子的因变量进行拓展。
五.对比和心得体会
关于代码
之前总是觉得60行代码的限制太死,甚至为了满足不超过60行的要求而在许多细节上修改好久,但是后来觉得其实还是自己的思路没有转换过来,仍然有大量面向过程的思想。自己从当年写C开始因为懒于传递参数而养成的一main到底的坏习惯其实并没有改变,只是为了调试方便,而对功能不同的部分采用了模块化处理,现在只是把不同的模块放到了不同的函数里而已。对于那些输入检索,输出等较为复杂的内容,依然是一个方法下来,有时行数超标就硬生生截成两段。造成的直接后果就是,当这次作业3与作业2相比要在某些功能上做一些细节上的改动时,面对功能下浩浩荡荡的数十行代码依然无从下手,甚至许多地方都忘了改,导致了不少错误。
我认为在这里有几个改进的方向。
- 培养面向对象的思维,写代码前认真分析架构,在脑中有明确思路时再动手,防止代码功能重复或遗漏,同时也防止在某些功能上过度纠结,改来改去。
- 借鉴上学期计组课设时的经验,在高内聚低耦合上下功夫,将功能细化、拆分,宁愿牺牲一部分简洁性与整体性,换来代码更好的结构与更低的维护成本。同时极大地提高代码的复用性,不像这次仅仅因为增加了嵌套,就彻底重写了多项式与单项式两个类的代码,还增加了两个三角函数类。
- 将代码更多的作为许多零件而非一个整体,剔除掉脑海中为了实现某个功能而写这整个代码的思想,提高代码的可拓展性,虽然写起来会变得复杂,但却可以显著降低未来的工作量。
关于bug
在提交后,尽管被hack次数不少,但实际的bug都十分集中,其一是在复用代码时没有考虑新的需要。其二是思路不够明确导致部分代码出现逻辑错误。
- 直接原因在于构造的测试数据不够全面,有些bug只有在数据有足够针对性的情况下才能发现,但是在不清楚bug的情况下针对性就无从谈起。归根结底还是除了给出的基本样例与自己乱编的样例之外没有更好的测试数据。
- 主要原因在于写代码过程中思维不能很好地驾驭整体代码,尤其是在部分内容已经遗忘的前提下依靠大脑强行进行整体把握难度较大。
- 根本原因在于没有一个足够清晰的思路,在架构不明确的情况下就开始写代码,还是像以前一样一边写代码一边改,有些功能重复实现,有些功能有相互推诿,经常搬起石头砸自己的脚。
Bug是不可避免的,不清楚bug就没有针对性测试数据,没有针对性数据就测不出bug,似乎陷入了一个恶性循环。但是办法总是有的。
- 先明确问题,头脑清晰写出的代码才能条理清晰。
- 培养面向对象的思想,先架构再编程。
- 从拿到指导书开始,就应该对于自己发现的难点与易错点及时记录,对于写程序过程中发现的可能出现的问题也及时记录,有针对性的构造测试数据。
关于性能分
个人认为尽管性能分占到了20%,但是其作用仍然应该是锦上添花,而非雪中送炭,甚至只要保证了自己的程序正确性,完全不化简也并非不可以。进行化简至多可以多得到20分,而出现一个bug就会失去整个测试点的得分,因此个人认为在时间与能力并不充裕的情况下,化简要遵循“简单有效”的原则。
简单,一方面化简部分尽量独立于输入输出求导等其他部分之外,降低程序的整体性。另一方面使化简的代码尽量简单,对于复杂容易出错的化简,大可舍弃,因为化简而造成的bug大多在分数上就是得不偿失的,还不算因此损失的时间和精力。
有效,是指化简后可以对性能产生较为显著的影响,而相应的代码量与复杂度相对较低。
- 对于第一次作业,因为较为简单,因此所有能想到的点都可以化简,实现起来也并不复杂。
- 对于第二次作业而言,显然合并同类项是最有效的化简方法,使首项为正尽管只能减少一个字符,但是在第一次的基础上实现起来非常简单,因此也可加入。而对于利用恒等式进行三角函数间的互相转化则要仔细考虑,在没有一个明确的思路的情况下不写反而比硬上要好得多。
- 对于第三次作业,可以化简的点非常多,但是难度也相应较大,因此更应做出谨慎的选择。比如去掉链式法则带来的大量的“1*”,输出时如果只有一项就去掉括号等,而诸如sin括号内为负时将符号提出等化简方法,就因为过于复杂而收效甚微可以直接放弃。