Android传感器 设备坐标系到世界坐标系的转换 分析以及应用
首先分别介绍两种坐标系的不同之处:
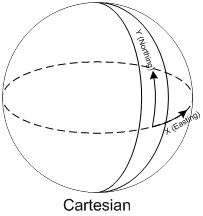
世界坐标系:
Y轴:和地球表面正切,并且指向磁北极
Z轴:和地球表面垂直,然后指向地球的中心
X轴:和Y,Z垂直,并且几乎是直接指向磁东
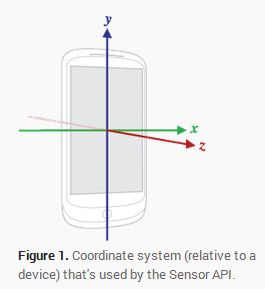
设备坐标系:
这个很好理解,垂直手机屏幕那一面向上为Z轴,向右为x,垂直于XZ面的即为Y轴。看图应该更清楚了。
由设备坐标转换为世界坐标:
将得到的原始传感器值(即设备坐标下的值)和坐标轴的旋转矩阵相乘即可。
如何得到旋转矩阵?
Android提供了一个现成的方法:
SensorManager.getRotationMatrix(R,I,gravityRawValues,magFieldRawValue);
官方这么写的
Computes the inclination matrix I as well as the rotation matrix R transforming a vector from the device coordinate system to the world’s coordinate system which is defined as a direct orthonormal basis, where:
就是传入设备坐标系下重力向量和磁场向量,就能得到一个矩阵R,能够从设备坐标系转换到世界坐标系的矩阵,以及一个矩阵I(倾斜矩阵与今天话题无关,不提)。
重力和磁力向量怎么来呢?
Android提供了现成的重力传感器TYPE_GRAVITY,可以直接注册监听来获取。不过其实这个重力传感器和方向传感器一样,是一个虚拟传感器,实际也是通过加速度计低通滤波之后拿到的。
(低通滤波过滤加速度计的非重力因素导致的加速度变化)
磁场向量比较容易,系统直接可以提供。
getRotationMatrix核心方法解析
旋转矩阵的计算思路:其实这个是“变基”了,从原来的设备坐标系的基转换为世界坐标系,那么计算出世界坐标系的三个坐标轴的单位向量在设备坐标系下的向量值,然后按行顺序依次填入3*3或者4*4的矩阵内,即可得到相应的旋转矩阵。
之所以可以这样求出旋转矩阵,可以这么理解:由矩阵运算规则,表示世界坐标系X的矩阵和任意一个向量A做积的和,几何上看,这就是投影啊,求的就是向量A投影到世界坐标系X上的长度,也就是向量A在世界坐标系下的x分量的值,同理求出y分量和z分量,就完成了设备坐标系和世界坐标系的转换啦
那么现在的问题就是如何得到在设备坐标系下的世界坐标系的三个坐标轴的单位向量
这里有两个假设
1. 传入的地磁场的向量在由重力和磁北极构成的平面之内
2. 传入的重力向量指向的是地心
官方文档也给出这样的说明:
The matrices returned by this function are meaningful only when the device is not free-falling and it is not close to the magnetic north. If the device is accelerating, or placed into a strong magnetic field, the returned matrices may be inaccurate.
不允许设备处于自由落体并且不是接近磁北极。如果设备处于加速状态或者强磁场中,返回的旋转矩阵就不可靠了。
为什么有这样的限制?
主要和计算原理有关系:
首先由地磁场向量和重力向量可以得到一个平面A,而地磁场向量和重力向量叉乘积可以得到垂直于平面A的一个向量,这个向量代表的就是地磁以东这个向量(在设备坐标系之下的地磁东),也就是世界坐标系X轴在设备坐标系下的向量。
同理,再由地磁东向量和重力向量向量的叉乘积就可以得到指向磁南极的向量了。也就是世界坐标系Y轴在设备坐标系下的向量。
而Z轴就是重力向量了。
然后把单位化之后的三个世界坐标系的向量值依次填入矩阵内就可以得到“设备坐标系到世界坐标系”的旋转矩阵了。
加了注释的源码:
public static boolean getRotationMatrix(float[] R, float[] I,
float[] gravity, float[] geomagnetic) {
// TODO: move this to native code for efficiency
float Ax = gravity[0];
float Ay = gravity[1];
float Az = gravity[2];
final float normsqA = (Ax*Ax + Ay*Ay + Az*Az);
final float g = 9.81f;
final float freeFallGravitySquared = 0.01f * g * g;
if (normsqA < freeFallGravitySquared) {
// gravity less than 10% of normal value
return false;
}
final float Ex = geomagnetic[0];
final float Ey = geomagnetic[1];
final float Ez = geomagnetic[2];
float Hx = Ey*Az - Ez*Ay;//H是东。计算磁场和地面两个向量的的叉乘积,就是东了
float Hy = Ez*Ax - Ex*Az;
float Hz = Ex*Ay - Ey*Ax;
final float normH = (float)Math.sqrt(Hx*Hx + Hy*Hy + Hz*Hz);//得到东方向量的大小normH
if (normH < 0.1f) {
// device is close to free fall (or in space?), or close to
// magnetic north pole. Typical values are > 100.
return false;
}
final float invH = 1.0f / normH;
Hx *= invH;//得到指向东的单位向量
Hy *= invH;
Hz *= invH;
final float invA = 1.0f / (float)Math.sqrt(Ax*Ax + Ay*Ay + Az*Az);
Ax *= invA;//同理得到指向地心的单位向量大小
Ay *= invA;
Az *= invA;
final float Mx = Ay*Hz - Az*Hy;//将指向磁东和地心的单位向量做叉乘,得到指向磁北的向量
final float My = Az*Hx - Ax*Hz;
final float Mz = Ax*Hy - Ay*Hx;
if (R != null) {
if (R.length == 9) {
R[0] = Hx; R[1] = Hy; R[2] = Hz;
R[3] = Mx; R[4] = My; R[5] = Mz;
R[6] = Ax; R[7] = Ay; R[8] = Az;
} else if (R.length == 16) {
R[0] = Hx; R[1] = Hy; R[2] = Hz; R[3] = 0;
R[4] = Mx; R[5] = My; R[6] = Mz; R[7] = 0;
R[8] = Ax; R[9] = Ay; R[10] = Az; R[11] = 0;
R[12] = 0; R[13] = 0; R[14] = 0; R[15] = 1;
}
}
.....
return true;
}一些现实的坑
上面的方法的确看上去挺完美的呢,但是!
磁力和加速度传感器的数值还是很容易收到外界干扰的。设备又没有额外的方式来区分到底是地磁还是电脑造成的干扰(就像人类不能抓着头发进行自举)。
磁场传感器倒是提供了一个获取磁场“可信度”的方法,但是目测只是根据数值的合理程度来给出评价,而不是我们想要的区分地磁和其他磁场干扰。
绕八字校准?个人推测照样也是看可信度而已。
而加速度的话,前面已经提到了,用低通或者系统自带的重力传感器,倒是还好。
所以应该要考虑从数据处理上解决这个问题呢。
Android:“我能怎么办,我也很绝望呀”
具体应用:
说了这么多,那有什么用呢?用处就是标准化磁场或传感器数值。我们知道设备坐标系下的数值基本是没有意义的,因为xyz三个轴的数值完全和设备当前的朝向有关系。而世界坐标系就提供了一个标准化数值的方法。
一个例子就是将计步器的值通过这个办法标准化之后,就可以无视手机朝向来获取比较稳定的世界坐标系下Z轴(即重力方向)的加速度值,对于计步是很有帮助的。
另外在标准化的磁场的时候,还碰到了一件趣事,就是转换为世界坐标系之后磁场三个轴坐标,X轴基本都是0是只有10^-6的一个极小的接近0的数值,其他YZ两个轴数值正常 。
来说下原因:
设MAG是待转换的设备坐标下的磁场向量,R是3*3的由上面方法得到的一个设备坐标到世界坐标的一个旋转矩阵,X是世界坐标下的的磁场向量的指向磁东的分量。那么根据矩阵乘法运算规则:
X = R[0] * MAG[0] + R[1] * MAG[1] + R[2] * MAG[2];
而由getRotationMatrix的源码可知R[0] R[1] R[2]的值就是设备坐标系下指向磁东的向量A,而MAG是指向地心和指向地磁南极的平面B内的一个向量C。
向量A垂直于平面B,所以向量A垂直于向量C,所以两向量积X=A*C就应该是0。
一个相对直观的理解就是,因为前提假设是传入的原始磁场向量是在地心和磁南极的平面内,所以就不可能有指向磁东的向量存在。所以经过变换之后的世界坐标系下也不会有磁东的向量存在了。
参考:
http://stackoverflow.com/questions/15315129/convert-magnetic-field-x-y-z-values-from-device-into-global-reference-frame
http://blog.sciencenet.cn/blog-254499-737232.html