特征选择
(1)什么是特征选择
特征选择 ( FeatureSelection )也称特征子集选择(Feature Subset Selection , FSS ) ,或属性选择( AttributeSelection ) ,是指从全部特征中选取一个特征子集,使构造出来的模型更好。
(2)为什么要做特征选择
在机器学习的实际应用中,特征数量往往较多,其中可能存在不相关的特征,特征之间也可能存在相互依赖,容易导致如下的后果:
Ø 特征个数越多,分析特征、训练模型所需的时间就越长。
Ø 特征个数越多,容易引起“维度灾难”,模型也会越复杂,其推广能力会下降。
特征选择能剔除不相关(irrelevant)或亢余(redundant)的特征,从而达到减少特征个数,提高模型精确度,减少运行时间的目的。另一方面,选取出真正相关的特征简化了模型,使研究人员易于理解数据产生的过程。
2 特征选择过程
2.1 特征选择的一般过程
特征选择的一般过程可用图1表示。首先从特征全集中产生出一个特征子集,然后用评价函数对该特征子集进行评价,评价的结果与停止准则进行比较,若评价结果比停止准则好就停止,否则就继续产生下一组特征子集,继续进行特征选择。选出来的特征子集一般还要验证其有效性。
综上所述,特征选择过程一般包括产生过程,评价函数,停止准则,验证过程,这4个部分。
(1) 产生过程(Generation Procedure )
产生过程是搜索特征子集的过程,负责为评价函数提供特征子集。搜索特征子集的过程有多种,将在2.2小节展开介绍。
(2) 评价函数(Evaluation Function )
评价函数是评价一个特征子集好坏程度的一个准则。评价函数将在2.3小节展开介绍。
(3) 停止准则(Stopping Criterion )
停止准则是与评价函数相关的,一般是一个阈值,当评价函数值达到这个阈值后就可停止搜索。
(4) 验证过程(Validation Procedure )
在验证数据集上验证选出来的特征子集的有效性。
![]()
图1. 特征选择的过程 ( M.Dash and H. Liu 1997 )
2.2 产生过程
产生过程是搜索特征子空间的过程。搜索的算法分为完全搜索(Complete),启发式搜索(Heuristic),随机搜索(Random)3大类,如图2所示。
![]()
图2. 产生过程算法分类 ( M.Dash and H. Liu 1997 )
下面对常见的搜索算法进行简单介绍。
2.2.1完全搜索
完全搜索分为穷举搜索(Exhaustive)与非穷举搜索(Non-Exhaustive)两类。
(1)广度优先搜索(Breadth First Search )
算法描述:广度优先遍历特征子空间。
算法评价:枚举了所有的特征组合,属于穷举搜索,时间复杂度是O(2n),实用性不高。
(2)分支限界搜索(Branch and Bound )
算法描述:在穷举搜索的基础上加入分支限界。例如:若断定某些分支不可能搜索出比当前找到的最优解更优的解,则可以剪掉这些分支。
(3)定向搜索(Beam Search )
算法描述:首先选择N个得分最高的特征作为特征子集,将其加入一个限制最大长度的优先队列,每次从队列中取出得分最高的子集,然后穷举向该子集加入1个特征后产生的所有特征集,将这些特征集加入队列。
(4)最优优先搜索( Best First Search )
算法描述:与定向搜索类似,唯一的不同点是不限制优先队列的长度。
2.2.2启发式搜索
(1)序列前向选择(SFS , Sequential Forward Selection )
算法描述:特征子集X从空集开始,每次选择一个特征x加入特征子集X,使得特征函数J( X)最优。简单说就是,每次都选择一个使得评价函数的取值达到最优的特征加入,其实就是一种简单的贪心算法。
算法评价:缺点是只能加入特征而不能去除特征。例如:特征A完全依赖于特征B与C,可以认为如果加入了特征B与C则A就是多余的。假设序列前向选择算法首先将A加入特征集,然后又将B与C加入,那么特征子集中就包含了多余的特征A。
(2)序列后向选择(SBS , Sequential Backward Selection )
算法描述:从特征全集O开始,每次从特征集O中剔除一个特征x,使得剔除特征x后评价函数值达到最优。
算法评价:序列后向选择与序列前向选择正好相反,它的缺点是特征只能去除不能加入。
另外,SFS与SBS都属于贪心算法,容易陷入局部最优值。
(3)双向搜索(BDS , Bidirectional Search )
算法描述:使用序列前向选择(SFS)从空集开始,同时使用序列后向选择(SBS)从全集开始搜索,当两者搜索到一个相同的特征子集C时停止搜索。
双向搜索的出发点是 ![]() 。如下图所示,O点代表搜索起点,A点代表搜索目标。灰色的圆代表单向搜索可能的搜索范围,绿色的2个圆表示某次双向搜索的搜索范围,容易证明绿色的面积必定要比灰色的要小。
。如下图所示,O点代表搜索起点,A点代表搜索目标。灰色的圆代表单向搜索可能的搜索范围,绿色的2个圆表示某次双向搜索的搜索范围,容易证明绿色的面积必定要比灰色的要小。
![]()
图2. 双向搜索
(4)增L去R选择算法( LRS , Plus-L Minus-R Selection )
该算法有两种形式:
<1> 算法从空集开始,每轮先加入L个特征,然后从中去除R个特征,使得评价函数值最优。( L> R )
<2> 算法从全集开始,每轮先去除R个特征,然后加入L个特征,使得评价函数值最优。( L< R )
算法评价:增L去R选择算法结合了序列前向选择与序列后向选择思想, L与R的选择是算法的关键。
(5)序列浮动选择(Sequential Floating Selection )
算法描述:序列浮动选择由增L去R选择算法发展而来,该算法与增L去R选择算法的不同之处在于:序列浮动选择的L与R不是固定的,而是“浮动”的,也就是会变化的。
序列浮动选择根据搜索方向的不同,有以下两种变种。
<1>序列浮动前向选择(SFFS , Sequential Floating Forward Selection )
算法描述:从空集开始,每轮在未选择的特征中选择一个子集x,使加入子集x后评价函数达到最优,然后在已选择的特征中选择子集z,使剔除子集z后评价函数达到最优。
<2>序列浮动后向选择(SFBS , Sequential Floating Backward Selection )
算法描述:与SFFS类似,不同之处在于SFBS是从全集开始,每轮先剔除特征,然后加入特征。
算法评价:序列浮动选择结合了序列前向选择、序列后向选择、增L去R选择的特点,并弥补了它们的缺点。
(6)决策树(Decision Tree Method , DTM)
算法描述:在训练样本集上运行C4.5或其他决策树生成算法,待决策树充分生长后,再在树上运行剪枝算法。则最终决策树各分支处的特征就是选出来的特征子集了。决策树方法一般使用信息增益作为评价函数。
2.2.3随机算法
(1)随机产生序列选择算法(RGSS, Random Generation plus SequentialSelection)
算法描述:随机产生一个特征子集,然后在该子集上执行SFS与SBS算法。
算法评价:可作为SFS与SBS的补充,用于跳出局部最优值。
(2)模拟退火算法(SA, Simulated Annealing )
模拟退火算法可参考 大白话解析模拟退火算法 。
算法评价:模拟退火一定程度克服了序列搜索算法容易陷入局部最优值的缺点,但是若最优解的区域太小(如所谓的“高尔夫球洞”地形),则模拟退火难以求解。
(3)遗传算法(GA, Genetic Algorithms )
遗传算法可参考 遗传算法入门 。
算法描述:首先随机产生一批特征子集,并用评价函数给这些特征子集评分,然后通过交叉、突变等操作繁殖出下一代的特征子集,并且评分越高的特征子集被选中参加繁殖的概率越高。这样经过N代的繁殖和优胜劣汰后,种群中就可能产生了评价函数值最高的特征子集。
随机算法的共同缺点:依赖于随机因素,有实验结果难以重现。
2.3 评价函数
评价函数的作用是评价产生过程所提供的特征子集的好坏。
评价函数根据其工作原理,主要分为筛选器(Filter)、封装器(Wrapper )两大类。
筛选器通过分析特征子集内部的特点来衡量其好坏。筛选器一般用作预处理,与分类器的选择无关。筛选器的原理如下图3:
![]()
图3.Filter原理(Ricardo Gutierrez-Osuna 2008 )
封装器实质上是一个分类器,封装器用选取的特征子集对样本集进行分类,分类的精度作为衡量特征子集好坏的标准。封装器的原理如图4所示。
![]()
图4.Wrapper原理 (Ricardo Gutierrez-Osuna 2008 )
下面简单介绍常见的评价函数。
(1) 相关性(Correlation)
运用相关性来度量特征子集的好坏是基于这样一个假设:好的特征子集所包含的特征应该是与分类的相关度较高(相关度高),而特征之间相关度较低的(亢余度低)。
可以使用线性相关系数(correlationcoefficient) 来衡量向量之间线性相关度。
![]()
( 2) 距离(Distance Metrics )
运用距离度量进行特征选择是基于这样的假设:好的特征子集应该使得属于同一类的样本距离尽可能小,属于不同类的样本之间的距离尽可能远。
常用的距离度量(相似性度量)包括欧氏距离、标准化欧氏距离、马氏距离等。
(3) 信息增益(Information Gain )
假设存在离散变量Y,Y中的取值包括{y1,y2,....,ym},yi出现的概率为Pi。则Y的信息熵定义为:
![]()
信息熵有如下特性:若集合Y的元素分布越“纯”,则其信息熵越小;若Y分布越“紊乱”,则其信息熵越大。在极端的情况下:若Y只能取一个值,即P1=1,则H(Y)取最小值0;反之若各种取值出现的概率都相等,即都是1/m,则H(Y)取最大值log2m。
在附加条件另一个变量X,而且知道X=xi后,Y的条件信息熵(Conditional Entropy)表示为:
![]()
在加入条件X前后的Y的信息增益定义为
![]()
类似的,分类标记C的信息熵H( C )可表示为:
![]()
将特征Fj用于分类后的分类C的条件信息熵H( C| Fj )表示为:
![]()
选用特征Fj前后的C的信息熵的变化成为C的信息增益(Information Gain),用![]() 表示,公式为:
表示,公式为:
![]()
假设存在特征子集A和特征子集B,分类变量为C,若IG(C|A ) > IG( C|B ) ,则认为选用特征子集A的分类结果比B好,因此倾向于选用特征子集A。
(4)一致性(Consistency )
若样本1与样本2属于不同的分类,但在特征A、 B上的取值完全一样,那么特征子集{A,B}不应该选作最终的特征集。
(5)分类器错误率(Classifier error rate )
使用特定的分类器,用给定的特征子集对样本集进行分类,用分类的精度来衡量特征子集的好坏。
以上5种度量方法中,相关性、距离、信息增益、一致性属于筛选器,而分类器错误率属于封装器。
筛选器由于与具体的分类算法无关,因此其在不同的分类算法之间的推广能力较强,而且计算量也较小。而封装器由于在评价的过程中应用了具体的分类算法进行分类,因此其推广到其他分类算法的效果可能较差,而且计算量也较大。
数据挖掘方法的提出,让人们有能力最终认识数据的真正价值,即蕴藏在数据中的信息和知识。数据挖掘 (DataMiriing),指的是从大型数据库或数据仓库中提取人们感兴趣的知识,这些知识是隐含的、事先未知的潜在有用信息,数据挖掘是目前国际上,数据库和信息决策领域的最前沿研究方向之一。因此分享一下很久以前做的一个小研究成果。也算是一个简单的数据挖掘处理的例子。
1.数据挖掘与聚类分析概述
数据挖掘一般由以下几个步骤:
(l)分析问题:源数据数据库必须经过评估确认其是否符合数据挖掘标准。以决定预期结果,也就选择了这项工作的最优算法。
(2)提取、清洗和校验数据:提取的数据放在一个结构上与数据模型兼容的数据库中。以统一的格式清洗那些不一致、不兼容的数据。一旦提取和清理数据后,浏览所创建的模型,以确保所有的数据都已经存在并且完整。
(3)创建和调试模型:将算法应用于模型后产生一个结构。浏览所产生的结构中数据,确认它对于源数据中“事实”的准确代表性,这是很重要的一点。虽然可能无法对每一个细节做到这一点,但是通过查看生成的模型,就可能发现重要的特征。
(4)查询数据挖掘模型的数据:一旦建立模型,该数据就可用于决策支持了。
(5)维护数据挖掘模型:数据模型建立好后,初始数据的特征,如有效性,可能发生改变。一些信息的改变会对精度产生很大的影响,因为它的变化影响作为基础的原始模型的性质。因而,维护数据挖掘模型是非常重要的环节。
聚类分析是数据挖掘采用的核心技术,成为该研究领域中一个非常活跃的研究课题。聚类分析基于”物以类聚”的朴素思想,根据事物的特征,对其进行聚类或分类。作为数据挖掘的一个重要研究方向,聚类分析越来越得到人们的关注。聚类的输入是一组没有类别标注的数据,事先可以知道这些数据聚成几簇爪也可以不知道聚成几簇。通过分析这些数据,根据一定的聚类准则,合理划分记录集合,从而使相似的记录被划分到同一个簇中,不相似的数据划分到不同的簇中。
2.特征选择与聚类分析算法
Relief为一系列算法,它包括最早提出的Relief以及后来拓展的ReliefF和RReliefF,其中RReliefF算法是针对目标属性为连续值的回归问题提出的,下面仅介绍一下针对分类问题的Relief和ReliefF算法。
2.1 Relief算法
Relief算法最早由Kira提出,最初局限于两类数据的分类问题。Relief算法是一种特征权重算法(Feature weighting algorithms),根据各个特征和类别的相关性赋予特征不同的权重,权重小于某个阈值的特征将被移除。Relief算法中特征和类别的相关性是基于特征对近距离样本的区分能力。算法从训练集D中随机选择一个样本R,然后从和R同类的样本中寻找最近邻样本H,称为Near Hit,从和R不同类的样本中寻找最近邻样本M,称为NearMiss,然后根据以下规则更新每个特征的权重:如果R和Near Hit在某个特征上的距离小于R和Near Miss上的距离,则说明该特征对区分同类和不同类的最近邻是有益的,则增加该特征的权重;反之,如果R和Near Hit在某个特征的距离大于R和Near Miss上的距离,说明该特征对区分同类和不同类的最近邻起负面作用,则降低该特征的权重。以上过程重复m次,最后得到各特征的平均权重。特征的权重越大,表示该特征的分类能力越强,反之,表示该特征分类能力越弱。Relief算法的运行时间随着样本的抽样次数m和原始特征个数N的增加线性增加,因而运行效率非常高。具体算法如下所示:
2.2 ReliefF算法
由于Relief算法比较简单,但运行效率高,并且结果也比较令人满意,因此得到广泛应用,但是其局限性在于只能处理两类别数据,因此1994年Kononeill对其进行了扩展,得到了ReliefF作算法,可以处理多类别问题。该算法用于处理目标属性为连续值的回归问题。ReliefF算法在处理多类问题时,每次从训练样本集中随机取出一个样本R,然后从和R同类的样本集中找出R的k个近邻样本(near Hits),从每个R的不同类的样本集中均找出k个近邻样本(near Misses),然后更新每个特征的权重,如下式所示:
Relief系列算法运行效率高,对数据类型没有限制,属于一种特征权重算法,算法会赋予所有和类别相关性高的特征较高的权重,所以算法的局限性在于不能有效的去除冗余特征。
2.3 K-means聚类算法
由于聚类算法是给予数据自然上的相似划法,要求得到的聚类是每个聚类内部数据尽可能的相似而聚类之间要尽可能的大差异。所以定义一种尺度来衡量相似度就显得非常重要了。一般来说,有两种定义相似度的方法。第一种方法是定义数据之间的距离,描述的是数据的差异。第二种方法是直接定义数据之间的相似度。下面是几种常见的定义距离的方法:
1.Euclidean距离,这是一种传统的距离概念,适合于2、3维空间。
2.Minkowski距离,是Euclidean距离的扩展,可以理解为N维空间的距离。
聚类算法有很多种,在需要时可以根据所涉及的数据类型、聚类的目的以及具的应用要求来选择合适的聚类算法。下面介绍 K-means聚类算法:
K-means算法是一种常用的基于划分的聚类算法。K-means算法是以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。K-means的处理过程为:首先随机选择k个对象作为初始的k个簇的质心;然后将余对象根据其与各个簇的质心的距离分配到最近的簇;最后重新计算各个簇的质心。不断重复此过程,直到目标函数最小为止。簇的质心由公式下列式子求得:
在具体实现时,为了防止步骤2中的条件不成立而出现无限循环,往往定义一个最大迭代次数。K-means尝试找出使平方误差函数值最小的k个划分。当数据分布较均匀,且簇与簇之间区别明显时,它的效果较好。面对大规模数据集,该算法是相对可扩展的,并且具有较高的效率。其中,n为数据集中对象的数目,k为期望得到的簇的数目,t为迭代的次数。通常情况下,算法会终止于局部最优解。但用,例如涉及有非数值属性的数据。其次,这种算法要求事先给出要生成的簇的数目k,显然这对用户提出了过高的要求,并且由于算法的初始聚类中心是随机选择的,而不同的初始中心对聚类结果有很大的影响。另外,K-means算法不适用于发现非凸面形状的簇,或者大小差别很大的簇,而且它对于噪音和孤立点数据是敏感的。
3.一个医学数据分析实例
3.1 数据说明
本文实验数据来自著名的UCI机器学习数据库,该数据库有大量的人工智能数据挖掘数据,网址为:http://archive.ics.uci.edu/ml/。该数据库是不断更新的,也接受数据的捐赠。数据库种类涉及生活、工程、科学各个领域,记录数也是从少到多,最多达几十万条。截止2010年底,数据库共有199个数据集,每个数据集合中有不同类型、时间的相关数据。可以根据实际情况进行选用。
本文选用的数据来类型为:Breast Cancer Wisconsin (Original) Data Set,中文名称为:威斯康星州乳腺癌数据集。这些数据来源美国威斯康星大学医院的临床病例报告,每条数据具有11个属性。下载下来的数据文件格式为“.data”,通过使用Excel和Matlab工具将其转换为Matlab默认的数据集保存,方便程序进行调用。
下表是该数据集的11个属性名称及说明:
对上述数据进行转换后,以及数据说明可知,可以用于特征提取的有9个指标,样品编号和分类只是用于确定分类。本文的数据处理思路是先采用ReliefF特征提取算法计算各个属性的权重,剔除相关性最小的属性,然后采用K-means聚类算法对剩下的属性进行聚类分析。
3.2 数据预处理与程序
本文在转换数据后,首先进行了预处理,由于本文的数据范围都是1-10,因此不需要归一化,但是数据样本中存在一些不完整,会影响实际的程序运行,经过程序处理,将这一部分数据删除。这些不完整的数据都是由于实际中一些原因没有登记或者遗失的,以“?”的形式代表。
本文采用Matlab软件进行编程计算。根据第三章提到的ReliefF算法过程,先编写ReliefF函数程序,用来计算特征属性,再编写主程序,在主程序中调用该函数进行计算,并对结果进行分析,绘图,得到有用的结论。
程序统一在最后贴出。
3.3 乳腺癌数据集特征提取
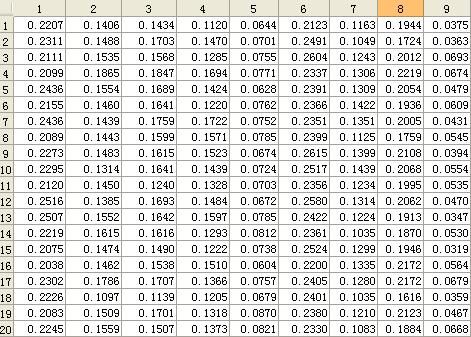
本文采用3.1节中的ReliefF算法来计算各个特征的权重,权重小于某个阈值的特征将被移除,针对本文的实际情况,将对权重最小的2-3种剔除。由于算法在运行过程中,会选择随机样本R,随机数的不同将导致结果权重有一定的出入,因此本文采取平均的方法,将主程序运行20次,然后将结果汇总求出每种权重的平均值。如下所示,列为属性编号,行为每一次的计算结果:
下面是特征提取算法计算的特征权重趋势图,计算20次的结果趋势相同:
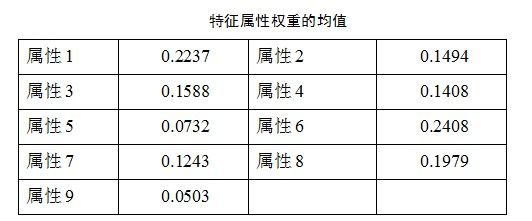
上述结果是否运行主程序所得的计算结果,看起来不直观,下面将其按照顺序绘图,可以直观显示各个属性权重的大小分布,如下图所示:
按照从小到大顺序排列,可知,各个属性的权重关系如下:
属性9<属性5<属性7<属性4<属性2<属性3<属性8<属性1<属性6
我们选定权重阀值为0.02,则属性9、属性4和属性5剔除。
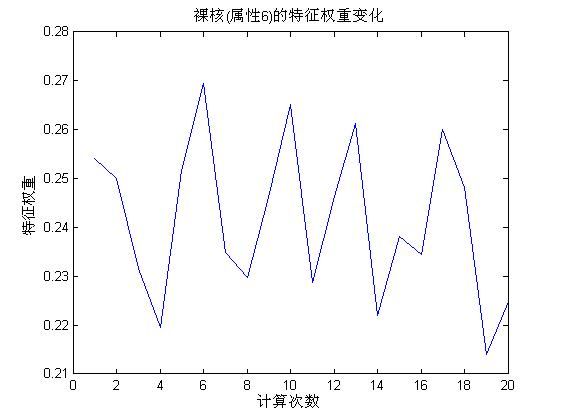
从上面的特征权重可以看出,属性6裸核大小是最主要的影响因素,说明乳腺癌患者的症状最先表现了裸核大小上,将直接导致裸核大小的变化,其次是属性1和属性8等,后几个属性权重大小接近,但是从多次计算规律来看,还是能够说明其中不同的重要程度,下面是着重对几个重要的属性进行分析。下面是20次测试中,裸核大小(属性6)的权重变化:
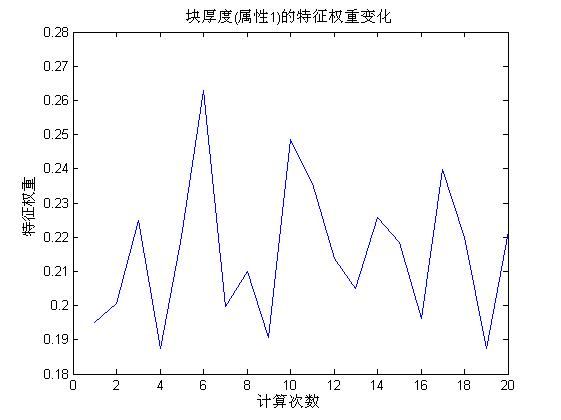
从上图中可以看到该属性权重大部分在0.22-0.26左右,是权重最大的一个属性。下面看看属性1的权重分布:
块厚度属性的特征权重在0.19-25左右变动,也是权重极高的一个,说明该特征属性在乳腺癌患者检测指标中是相当重要的一个判断依据。进一步分析显示,在单独对属性6,和属性1进行聚类分析,其成功率就可以达到91.8%。本文将在下节中的Kmeans算法中详细介绍。
3.4 乳腺癌数据集聚类分析
上一节中通过ReliefF算法对数据集的分析,可以得到属性权重的重要程度,这些可以对临床诊断有一些参考价值,可以用来对实际案例进行分析,可以尽量的避免错误诊断,并提高诊断的速度和正确率。下面将通过K-menas聚类分析算法对数据进行分析。本小节将分为几个步骤来进行对比,确定聚类分析算法的结果以及与ReliefF算法结合的结果等。
1.K-means算法单独分析数据集
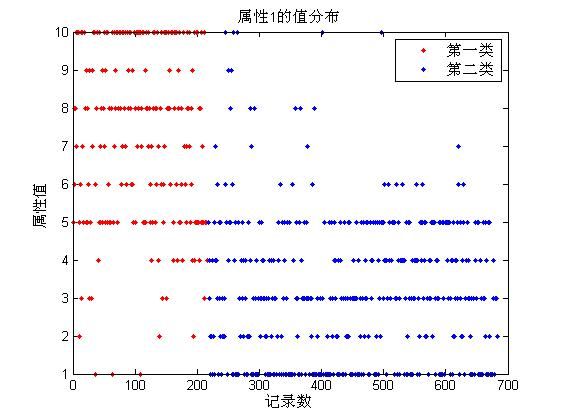
下面将采用Kmeans算法单独对数据集进行分析。Matlab中已经包括了一些常规数据挖掘的算法,例如本文所用到的K-means算法。该函数名为kmeans,可以对数据集进行聚类分析。首先本文对乳腺癌数据集的所有属性列(除去身份信息和分类列)直接进行分类,由于数据集结果只有2种类型,所以首先进行分2类的测试,结果如下:总体将683条数据分成了2类,总体的正确率为94.44%,其中第一类的正确率为93.56%,第二类的正确率为96.31%。下面是分类后对按照不同属性的绘制的属性值分布图:
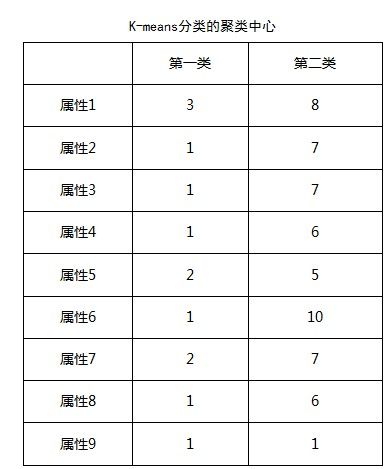
限于篇幅,只选择了上述3个特征属性进行图像绘制,从结果来看, 可以很直观的观察到K-means算法分类后的情况,第一类与第一类的分类界限比较清晰。但是不容易观察到正确和错误的情况。下表是分类结果中各个属性的聚类中心:
从K-means算法的效果来看,能够很准确的将数据集进行分类。一方面是由于该数据集,可能是该案例特征比较明显,另一方面是由于K-menas算法对这种2类的作用较大。
2.K-means结合ReliefF分析数据集
单从分类正确率和结果方面来看,K-mens算法已经完全可以对乳腺癌数据集做出非常准确的判断。但是考虑ReliefF算法对属性权重的影响,本小节将结合ReliefF算法和K-means算法来对该数据集进行分析,一方面得到处理该问题一些简单的结论,另外一方面可以得到一些对医学处理数据的方法研究方法。
首先,本小节首先根据3.2节中的一些结论,根据不同属性的权重来对k-menas分类数据进行预处理,以得到更精确的结论和对该数据更深度的特征规律。
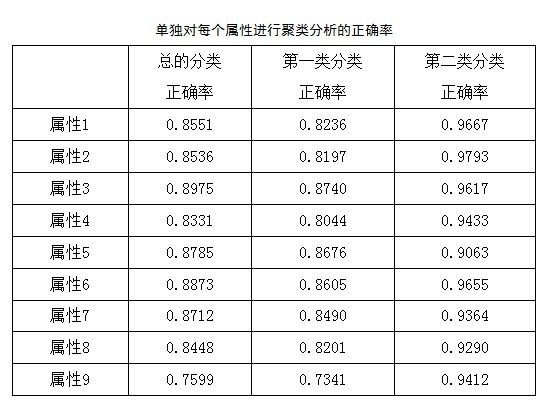
从3.2节中,得知属性9<属性5<属性7<属性4<属性2<属性3<属性8<属性1<属性6,根据ReliefF算法原理本文可以认为,对于这种属性6和属性1重要的特征属性,应该对分类起到更加到的作用。所以下面将单独对各个属性的数据进行分类测试,详细结果如下表:
总的分类正确率中,属性9最低,属性6最高,这与ReliefF算法测试的结果大致相似,但是由于ReliefFar算法中间部分权重接近,所以也区分不明显。说明特征属性权重的判断对分类是有影响的。上述单独分类中,只将需要分类的列数据取出来,输入到K-means算法中即可。由于输入数据的变化,K-means分类时结果肯定是有差距的,所以单独从一个属性判断其类型是不可靠的。下面选择了单个分类时最高和最低的情况,绘制其分类属性值分布图,如下图所示:
下面将对特征权重按照从大到小的顺序,选择相应的数据,进行聚类分析,结论如下:
1.直接选择全部9种属性,分类成功率为:94.44%;
2.选择属性6,属性1,分类成功率为:91.36%;
3.选择属性6,1,8,3,分类成功率为:93.85%;
4.选择属性6,1,8,3,2,4,分类成功率为:94.48%;
5.选择属性6,1,8,3,2,4,5,7,分类成功率为:95.02%;
从上面的测试可以看出,选择特征权重最大的6个属性,其正确率就达到选择所有属性的情况,因此我们可以认为特征权重最小的几个属性在乳腺癌诊断过程的作用实际可能比较小,实际有可能造成反作用,也就是这几个属性值与乳腺癌没有必然的联系。这一点可以给诊断参考,或者引起注意,进行进一步的研究,确认。
3. K-means分成3类的情况
虽然从上述2小节的实验中可以得到该数据集的大部分结果和结论。但是为了将相同类型的数据更加准确的分出,下面将尝试分为3类的情况。一方面,可以分析在乳腺癌良性和恶性情况下的显著特征属性;另一方面也可以根据此结果找到更加合理的解决方法。
还是采用Matlab中的kmeans函数,将分类数改为3,由于分为3类后数据类型增多,判断较复杂,所以手动对数据进行分析,将所有特征属性加入进去。运行结果如下,测试数据中总共683条,其中良性共444条,恶性共239条:
1.分为第一类的记录中,良性占96.88%;
2.分为第二类的记录中,恶性占 100% ;
3.分为第三类的记录中,恶性占 92%;
根据上述结果可以认为第一类为良性的分类,第二类为恶性分类,第三类为混合类。对于混合类,说明里面的数据较其他数据更加接近于偏离病例的典型数据,所以进一步分析在第一类中和第二类中的分类正确率:
1.第一类为良性,共448条数据,分类正确率为96.88%;
2.第二类为恶性,共99条数据,分类正确率为 100% ;
3.第三类为混合类,共136条数据
因此单独从分类后的正确率来看,效果有提高,说明对典型的病例数据分类更准确,但是对于第三类数据,而无法区分,因此这种情况下,其意义不在于分类的整体正确率,而在于在一些特殊情况下,可以根据一些重要的特征属性值就可以为患者确诊,从而提高效率和准确率,减少误诊断的几率。
上面是将所有属性进行K-means变换,下面将结合ReliefF算法,先去掉一部分特征权重较小的特征属性后,再进行K-means处理。根据4.2节中的结论,下面提取权重最大的6个属性进行测试,分别是:属性6,属性 1,属性 8,属性 3,属性2,属性 4。
1.第一类为良性,共281条数据,分类正确率为97.51% ;
2.第二类为恶性,共211条数据,分类正确率为 97.16% ;
3.第三类为混合类,共191条数据
因此,对比可以看到,虽然良性的正确率增加了,但是检测出的数据减少了。第三类混合的数量也增多了,说明提出了特种属性较小的属性,可以更加容易区分极端的病例数据,对极端数据的检测更加准确。
4.主要的Matlab源代码
1.ReliefF特征提取算法Matlab主程序
1 %主函数 2 clear;clc; 3 load('matlab.mat') 4 D=data(:,2:size(data,2));% 5 m =80 ;%抽样次数 6 k = 8; 7 N=20;%运行次数 8 for i =1:N 9 W(i,:) = ReliefF (D,m,k) ; 10 end 11 for i = 1:N %将每次计算的权重进行绘图,绘图N次,看整体效果 12 plot(1:size(W,2),W(i,:)); 13 hold on ; 14 end 15 for i = 1:size(W,2) %计算N次中,每个属性的平均值 16 result(1,i) = sum(W(:,i))/size(W,1) ; 17 end 18 xlabel('属性编号'); 19 ylabel('特征权重'); 20 title('ReliefF算法计算乳腺癌数据的特征权重'); 21 axis([1 10 0 0.3]) 22 %------- 绘制每一种的属性变化趋势 23 xlabel('计算次数'); 24 ylabel('特征权重'); 25 name =char('块厚度','细胞大小均匀性','细胞形态均匀性','边缘粘附力','单上皮细胞尺寸','裸核','Bland染色质','正常核仁','核分裂'); 26 name=cellstr(name); 27 28 for i = 1:size(W,2) 29 figure 30 plot(1:size(W,1),W(:,i)); 31 xlabel('计算次数') ; 32 ylabel('特征权重') ; 33 title([char(name(i)) '(属性' num2Str(i) ')的特征权重变化']); 34 end
2.ReliefF函数程序
1 %Relief函数实现 2 %D为输入的训练集合,输入集合去掉身份信息项目;k为最近邻样本个数 3 function W = ReliefF (D,m,k) 4 Rows = size(D,1) ;%样本个数 5 Cols = size(D,2) ;%特征熟练,不包括分类列 6 type2 = sum((D(:,Cols)==2))/Rows ; 7 type4 = sum((D(:,Cols)==4))/Rows ; 8 %先将数据集分为2类,可以加快计算速度 9 D1 = zeros(0,Cols) ;%第一类 10 D2 = zeros(0,Cols) ;%第二类 11 for i = 1:Rows 12 if D(i,Cols)==2 13 D1(size(D1,1)+1,:) = D(i,:) ; 14 elseif D(i,Cols)==4 15 D2(size(D2,1)+1,:) = D(i,:) ; 16 end 17 end 18 W =zeros(1,Cols-1) ;%初始化特征权重,置0 19 for i = 1 : m %进行m次循环选择操作 20 %从D中随机选择一个样本R 21 [R,Dh,Dm] = GetRandSamples(D,D1,D2,k) ; 22 %更新特征权重值 23 for j = 1:length(W) %每个特征累计一次,循环 24 W(1,j)=W(1,j)-sum(Dh(:,j))/(k*m)+sum(Dm(:,j))/(k*m) ;%按照公式更新权重 25 end 26 end
ReliefF辅助函数,寻找最近的样本数K
1 %获取随机R 以及找出邻近样本 2 %D:训练集;D1:类别1数据集;D2:类别2数据集; 3 %Dh:与R同类相邻的样本距离;Dm:与R不同类的相邻样本距离 4 function [R,Dh,Dm] = GetRandSamples(D,D1,D2,k) 5 %先产生一个随机数,确定选定的样本R 6 r = ceil(1 + (size(D,1)-1)*rand) ; 7 R=D(r,:); %将第r行选中,赋值给R 8 d1 = zeros(1,0) ;%先置0,d1是与R的距离,是不是同类在下面判断 9 d2 = zeros(1,0) ;%先置0,d2是与R的距离 10 %D1,D2是先传入的参数,在ReliefF函数中已经分类好了 11 for i =1:size(D1,1) %计算R与D1的距离 12 d1(1,i) = Distance(R,D1(i,:)) ; 13 end 14 for j = 1:size(D2,1)%计算R与D2的距离 15 d2(1,j) = Distance(R,D2(j,:)) ; 16 end 17 [v1,L1] = sort(d1) ;%d1排序, 18 [v2,L2] = sort(d2) ;%d2排序 19 if R(1,size(R,2))==2 %如果R样本=2,是良性 20 H = D1(L1(1,2:k+1),:) ; %L1中是与R最近的距离的编号,赋值给H。 21 M = D2(L2(1,1:k),:) ; %v2(1,1:k) ; 22 else 23 H = D1(L1(1,1:k),:); 24 M = D2(L2(1,2:k+1),:) ; 25 end 26 %循环计算每2个样本特征之间的特征距离:(特征1-特征2)/(max-min) 27 for i = 1:size(H,1) 28 for j =1 :size(H,2) 29 Dh(i,j) = abs(H(i,j)-R(1,j))/9 ; % 本文数据范围都是1-10,所以max-min=9为固定 30 Dm(i,j) = abs(M(i,j)-R(1,j))/9 ; 31 end 32 end
3.K-means算法主程序
1 clc;clear; 2 load('matlab.mat')%加载测试数据 3 N0 =1 ; %从多少列开始的数据进行预测分类 4 N1 = size(data,1);%所有数据的行数 5 data=data(N0:N1,:);%只选取需要测试的数据 6 data1=data(:,[2,3,4,5,6,7,8,9]);% [2,4,7,9] 2:size(data,2)-1 7 opts = statset('Display','final');%控制选项 8 [idx,ctrs,result,D] = kmeans(data1,2,... %data1为要分类的数据,2为分类的类别数,本文只有2类 9 'Distance','city',... %选择的距离的计算方式 10 'Options',opts); % 控制选项,参考matlab帮助 11 t=[data(:,size(data,2)),idx(:,1)];%把测试数据最后一列,也就是分类属性 和 分类结果取出来:列 + 列 12 d2 = data(idx==1,11);%提取原始数据中属于第1类的数据的最后一列 13 a = sum(d2==2) ; 14 b=a/length(d2) ; 15 totalSum = 0 ;%总的正确率 16 rate1 = 0 ;%第一类的判断正确率.分类类别中数据的正确性 17 rate2 = 0 ;%第二类的判断正确率. 18 if(b>0.5) %说明第1类属于良性,则a的值就是良性中判断正确的个数 19 totalSum = totalSum + a ; 20 rate1 = a/length(d2) ; 21 %然后加上恶性中判断正确的比例 22 totalSum = totalSum + sum(data(idx==2,11)==4) ; 23 rate2 = sum(data(idx==2,11)==4)/length(data(idx==2,11)) ; 24 else %说明第1类属于恶性 25 totalSum = totalSum + sum(data(idx==1,11)==4) ; 26 totalSum = totalSum + sum(data(idx==2,11)==2) ; 27 rate1 = sum(data(idx==2,11)==2)/length(data(idx==2,11)) ; 28 rate2 = sum(data(idx==1,11)==4)/length(data(idx==1,11)) ; 29 end 30 x1 =1;%第x1个属性 31 x2 =1 ;%第x2个属性 32 plot(1:sum(idx==1),data1(idx==1,x1),'r.','MarkerSize',12); 33 hold on ; 34 plot(sum(idx==1)+1:sum(idx==1)+sum(idx==2),data1(idx==2,x1),'b.','MarkerSize',12); 35 xlabel('记录数'); 36 ylabel('属性值'); 37 title('属性9的值分布'); 38 legend('第一类','第二类'); 39 axis([0 640 0 10]) 40 rate = totalSum/size(t,1) %总的判断准确率
在信息增益中,重要性的衡量标准就是看特征能够为分类系统带来多少信息,带来的信息越多,该特征越重要。
因此先回忆一下信息论中有关信息量(就是“熵”)的定义。说有这么一个变量X,它可能的取值有n多种,分别是x1,x2,……,xn,每一种取到的概率分别是P1,P2,……,Pn,那么X的熵就定义为:
![]()
意思就是一个变量可能的变化越多(反而跟变量具体的取值没有任何关系,只和值的种类多少以及发生概率有关),它携带的信息量就越大(因此我一直觉得我们的政策法规信息量非常大,因为它变化很多,基本朝令夕改,笑)。
对分类系统来说,类别C是变量,它可能的取值是C1,C2,……,Cn,而每一个类别出现的概率是P(C1),P(C2),……,P(Cn),因此n就是类别的总数。此时分类系统的熵就可以表示为:
![]()
有同学说不好理解呀,这样想就好了,文本分类系统的作用就是输出一个表示文本属于哪个类别的值,而这个值可能是C1,C2,……,Cn,因此这个值所携带的信息量就是上式中的这么多。
信息增益是针对一个一个的特征而言的,就是看一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即增益。系统含有特征t的时候信息量很好计算,就是刚才的式子,它表示的是包含所有特征时系统的信息量。
问题是当系统不包含t时,信息量如何计算?我们换个角度想问题,把系统要做的事情想象成这样:说教室里有很多座位,学生们每次上课进来的时候可以随便坐,因而变化是很大的(无数种可能的座次情况);但是现在有一个座位,看黑板很清楚,听老师讲也很清楚,于是校长的小舅子的姐姐的女儿托关系(真辗转啊),把这个座位定下来了,每次只能给她坐,别人不行,此时情况怎样?对于座次的可能情况来说,我们很容易看出以下两种情况是等价的:(1)教室里没有这个座位;(2)教室里虽然有这个座位,但其他人不能坐(因为反正它也不能参与到变化中来,它是不变的)。
对应到我们的系统中,就是下面的等价:(1)系统不包含特征t;(2)系统虽然包含特征t,但是t已经固定了,不能变化。
我们计算分类系统不包含特征t的时候,就使用情况(2)来代替,就是计算当一个特征t不能变化时,系统的信息量是多少。这个信息量其实也有专门的名称,就叫做“条件熵”,条件嘛,自然就是指“t已经固定“这个条件。
但是问题接踵而至,例如一个特征X,它可能的取值有n多种(x1,x2,……,xn),当计算条件熵而需要把它固定的时候,要把它固定在哪一个值上呢?答案是每一种可能都要固定一下,计算n个值,然后取均值才是条件熵。而取均值也不是简单的加一加然后除以n,而是要用每个值出现的概率来算平均(简单理解,就是一个值出现的可能性比较大,固定在它上面时算出来的信息量占的比重就要多一些)。
因此有这样两个条件熵的表达式:
![]()
这是指特征X被固定为值xi时的条件熵,
![]()
这是指特征X被固定时的条件熵,注意与上式在意义上的区别。从刚才计算均值的讨论可以看出来,第二个式子与第一个式子的关系就是:
![]()
具体到我们文本分类系统中的特征t,t有几个可能的值呢?注意t是指一个固定的特征,比如他就是指关键词“经济”或者“体育”,当我们说特征“经济”可能的取值时,实际上只有两个,“经济”要么出现,要么不出现。一般的,t的取值只有t(代表t出现)和![]() (代表t不出现),注意系统包含t但t 不出现与系统根本不包含t可是两回事。
(代表t不出现),注意系统包含t但t 不出现与系统根本不包含t可是两回事。
因此固定t时系统的条件熵就有了,为了区别t出现时的符号与特征t本身的符号,我们用T代表特征,而用t代表T出现,那么:
![]()
与刚才的式子对照一下,含义很清楚对吧,P(t)就是T出现的概率,![]() 就是T不出现的概率。这个式子可以进一步展开,其中的
就是T不出现的概率。这个式子可以进一步展开,其中的
![]()
另一半就可以展开为:
![]()
因此特征T给系统带来的信息增益就可以写成系统原本的熵与固定特征T后的条件熵之差:
![]()
公式中的东西看上去很多,其实也都很好计算。比如P(Ci),表示类别Ci出现的概率,其实只要用1除以类别总数就得到了(这是说你平等的看待每个类别而忽略它们的大小时这样算,如果考虑了大小就要把大小的影响加进去)。再比如P(t),就是特征T出现的概率,只要用出现过T的文档数除以总文档数就可以了,再比如P(Ci|t)表示出现T的时候,类别Ci出现的概率,只要用出现了T并且属于类别Ci的文档数除以出现了T的文档数就可以了。
从以上讨论中可以看出,信息增益也是考虑了特征出现和不出现两种情况,与开方检验一样,是比较全面的,因而效果不错。但信息增益最大的问题还在于它只能考察特征对整个系统的贡献,而不能具体到某个类别上,这就使得它只适合用来做所谓“全局”的特征选择(指所有的类都使用相同的特征集合),而无法做“本地”的特征选择(每个类别有自己的特征集合,因为有的词,对这个类别很有区分度,对另一个类别则无足轻重)。
看看,导出的过程其实很简单,没有什么神秘的对不对。可有的学术论文里就喜欢把这种本来很直白的东西写得很晦涩,仿佛只有读者看不懂才是作者的真正成功。
咱们是新一代的学者,咱们没有知识不怕被别人看出来,咱们有知识也不怕教给别人。所以咱都把事情说简单点,说明白点,大家好,才是真的好。