Day_25,数据结构扩张以红黑树为基础(将红黑树变更为区间树)
将红黑树扩张为区间树
我们还是按照扩张数据结构的四个步骤走:
①红黑树为基础数据结构
②节点的key改为区间i;给节点新增一个max附加信息,max为以该节点为根的子树(包括自身)的最大端点值
③在基础数据结构的基础操作上(例如插入、删除)能否维护附加信息详看下面(1)(2)(3)(4),其中(2)(3)(4)是对max的维护
④新增操作:获取树中是否有与给定区间重叠的区间
(1)区间树的创建:由之前的比较key改成比较i.low,即区间的左端点
下面三点是对max的维护
(2)插入:插入的时候仅需要维护插入节点node,以及node到根节点简单路径上的节点
(3)删除:根据上篇红黑树的删除可知,在删除过程中,会发生位置变动的就是 删除的节点 或者 删除节点的后继节点,因此维护也只需要维护这两个节点其中之一到根节点简单路径上的节点
(4)左右旋:通过观察下图可知,左右旋的过程中实际上只影响了x,y两个节点,因此只要维护这两个节点即可

上代码
下面仅列出有发生变化的函数以及新增的函数,其余部分查看上面文章
红黑树的实现及理解
#include (a[0],NILNode,NILNode,NILNode,NodeColor(BLACK));
//他在识别的时候 left!=right!=p 可能跟引用关系有关 改成&试试??
root = new RBTreeNode<T>(a[0]);
root->p = NILNode;
root->left = NILNode;
root->right = NILNode;
root->color = NodeColor(BLACK);
//大体思路,循环遍历
//小于找左孩子
//大于找右孩子
//孩子为空直接放置
//如果i==0 将root指针指向该节点
for (int i=1;i<length;i++)
{
Insert(a[i]);
}
}
template<class T>
RBSearchTree<T>::MidWalk()
{
RBTreeNode<T> *node = root;
MidWalkInner(node);
cout<<endl;
}
template<class T>
RBSearchTree<T>::MidWalkInner(RBTreeNode<T> *node)
{
if (node!=NILNode)
{
MidWalkInner(node->left);
cout<<"["<<node->i->low<<","<<node->i->high<<"]"<<" color is "<<node->color<<" p is "<<"["<<node->p->i->low<<","<<node->p->i->high<<"]"<<" max is "<<node->max<<endl;
MidWalkInner(node->right);
}
}
template<class T>
RBTreeNode<T> * RBSearchTree<T>::Search(Interval<T> *i)
{
RBTreeNode<T> *node = root;
while(node !=NILNode && (i->low > node->i->high || i->high < node->i->low))
{
if (node->left != NILNode && node->left->max >= i->low)
node = node->left;
else
node = node->right;
}
return node;
}
template<class T>
RBTreeNode<T> * RBSearchTree<T>::MinimumInner(RBTreeNode<T> *node)
{
while(node->left!=NILNode)
node = node->left;
return node;
}
template<class T>
string RBSearchTree<T>::Insert(Interval<T> *i)
{
RBTreeNode<T> *insertNode = new RBTreeNode<T>(i,NULL,NILNode,NILNode,NILNode,NodeColor(RED));
RBTreeNode<T> *insertNodeParent = NILNode;
RBTreeNode<T> *node = root;
while(node != NILNode)
{
insertNodeParent = node;
if (i->low <= node->i->low)
node = node->left;
else
node = node->right;
}
insertNode->p = insertNodeParent;
if (i->low <= insertNodeParent->i->low)
insertNodeParent->left = insertNode;
else
insertNodeParent->right = insertNode;
insertNode->left = NILNode;
insertNode->right = NILNode;
insertNode->color = NodeColor(RED);
CalMaxToRoot(insertNode);
RBTreeInsertFix(insertNode);
return strTrue;
}
template<class T>
RBSearchTree<T>::RBTreeInsertFix(RBTreeNode<T> *node)
{
while (node->p->color == NodeColor(RED))
{
if (node->p == node->p->p->left)
{
RBTreeNode<T> *y = node->p->p->right; //叔节点
if (y->color == NodeColor(RED))
{
node->p->color = NodeColor(BLACK);
node->p->p->color = NodeColor(RED);
y->color = NodeColor(BLACK);
node = node->p->p;
}
else if (node == node->p->right)
{
node = node->p;
LeftRotate(node);
}
else
{
node->p->color = NodeColor(BLACK);
node->p->p->color = NodeColor(RED);
RightRotate(node->p->p);
}
}
else
{
RBTreeNode<T> *y = node->p->p->left; //叔节点
if (y->color == NodeColor(RED))
{
node->p->color = NodeColor(BLACK);
node->p->p->color = NodeColor(RED);
y->color = NodeColor(BLACK);
node = node->p->p;
}
else if (node == node->p->left)
{
node = node->p;
RightRotate(node);
}
else
{
node->p->color = NodeColor(BLACK);
node->p->p->color = NodeColor(RED);
LeftRotate(node->p->p);
}
}
}
root->color = NodeColor(BLACK);
}
template<class T>
RBTreeNode<T> * RBSearchTree<T>::Maximum()
{
RBTreeNode<T> *node = root;
while(node->right!=NILNode)
node = node->right;
return node;
}
template<class T>
RBTreeNode<T> * RBSearchTree<T>::MaximumInner(RBTreeNode<T> *node)
{
while(node->right!=NILNode)
node = node->right;
return node;
}
template<class T>
RBTreeNode<T> * RBSearchTree<T>::TreePredecessor(RBTreeNode<T> *node)
{
if(node->left !=NILNode)
{
RBTreeNode<T> * temp = MaximumInner(node->left);
return temp;
}
RBTreeNode<T> * temp = node->p;
while( temp!=NILNode && node == temp->left)
{
node = temp;
temp = temp->p;
}
if (temp == NILNode)
temp = new RBTreeNode<T>(new Interval<T>(-1,-1)); //表示没有前驱
return temp;
}
template<class T>
RBTreeNode<T> * RBSearchTree<T>::TreeSuccessor(RBTreeNode<T> *node)
{
if(node->right !=NILNode)
{
RBTreeNode<T> * temp = MinimumInner(node->right);
return temp;
}
RBTreeNode<T> * temp = node->p;
while( temp!=NILNode && node == temp->right)
{
node = temp;
temp = temp->p;
}
if (temp == NILNode)
temp = new RBTreeNode<T>(new Interval<T>(-1,-1)); //表示没有后继
return temp;
}
template<class T>
string RBSearchTree<T>::Delete(Interval<T> *i)
{
RBTreeNode<T> *node = Search(i);//找到要删除的节点
RBTreeNode<T> *backupsNode; //备份指针,用于保存节点长度发生变化的节点(发生继承关系的节点)
RBTreeNode<T> *successorNode = NILNode; //用于保存后继节点的父节点,计算max用
NodeColor originColor = node->color;//记录原始颜色(如果删除的是黑色是会影响黑高的,红色则不会)
if(node->left==NILNode) //单左节点
{
backupsNode = node->right;
RBTransplant(node,node->right);
}
else if(node->right==NILNode)//单右节点
{
backupsNode = node->left;
RBTransplant(node,node->left);
}
else
{
//找到后继节点
RBTreeNode<T> *temp = MinimumInner(node->right);
originColor = temp->color;
if (temp->p == node)
backupsNode->p = temp;
else //if (temp->p != node)
{
RBTransplant(temp,temp->right);
temp->right = node->right;
temp->right->p = temp;
}
RBTransplant(node,temp);
temp->left = node->left;
temp->left->p = temp;
temp->color = node->color;
}
//如果删除的是在末节点,影响的还是只有他到root最简单路径上的点
//但是当删除的点不是末端节点的时候,影响的就是后继节点到root最简单路径上的点
if (successorNode==NILNode)
CalMaxToRoot(node);
else
CalMaxToRoot(successorNode);
if (originColor == NodeColor(BLACK))
RBTreeDeleteFix(backupsNode);
return strTrue;
}
template<class T>
RBSearchTree<T>::RBTreeDeleteFix(RBTreeNode<T> *node)
{
while (node != root && node->color == NodeColor(BLACK))
{
if (node == node->p->left)
{
RBTreeNode<T> *broNode = node->p->right;
if (broNode->color == NodeColor(RED))
{
broNode->color = NodeColor(BLACK);
node->p->color = NodeColor(RED);
LeftRotate(node->p);
broNode = node->p->right;
}
if (broNode->left->color == NodeColor(BLACK) &&broNode->right->color == NodeColor(BLACK))
{
node = node->p;
broNode->color = NodeColor(RED);
}
else if (broNode->left->color == NodeColor(RED))
{
broNode->left->color = NodeColor(BLACK);
broNode->color = NodeColor(RED);
RightRotate(broNode);
broNode = node->p->right;
}
else
{
broNode->right->color == NodeColor(BLACK);
broNode->color = broNode->p->color;
broNode->p->color = NodeColor(BLACK);
LeftRotate(node->p);
node = root;//用于终止循环
}
}
else
{
RBTreeNode<T> *broNode = node->p->left;
if (broNode->color == NodeColor(RED))
{
broNode->color = NodeColor(BLACK);
node->p->color = NodeColor(RED);
RightRotate(node->p);
broNode = node->p->left;
}
if (broNode->left->color == NodeColor(BLACK) &&broNode->right->color == NodeColor(BLACK))
{
node = node->p;
broNode->color = NodeColor(RED);
}
else if (broNode->right->color == NodeColor(RED))
{
broNode->right->color = NodeColor(BLACK);
broNode->color = NodeColor(RED);
RightRotate(broNode);
broNode = node->p->left;
}
else
{
broNode->left->color == NodeColor(BLACK);
broNode->color = broNode->p->color;
broNode->p->color = NodeColor(BLACK);
LeftRotate(node->p);
node = root;//用于终止循环
}
}
}
node->color = NodeColor(BLACK);
}
template<class T>
RBSearchTree<T>::LeftRotate(RBTreeNode<T> *node)
{
RBTreeNode<T> *y = node->right;
node->right = y->left;
if (y->left !=NILNode)
y->left->p = node;
y->p = node->p;
if (node->p == NILNode)
root = y;
else if (node->p->left == node)
node->p->left = y;
else
node->p->right = y;
y->left = node;
node->p = y;
CalMax(node);
CalMax(y);
}
template<class T>
RBSearchTree<T>::RightRotate(RBTreeNode<T> *node)
{
RBTreeNode<T> *y = node->left;
node->left = y->right;
if (y->right !=NILNode)
y->right->p = node;
y->p = node->p;
if (node->p == NILNode)
root = y;
else if (node->p->left == node)
node->p->left = y;
else
node->p->right = y;
y->right = node;
node->p = y;
CalMax(node);
CalMax(y);
}
template<class T>
RBSearchTree<T>::CalMaxToRoot(RBTreeNode<T> *node)
{
//这里可以做一个小优化,当删除的节点是root或者 node->i->high < node->p->max的时候,可以直接return
while(node->p !=NILNode)
{
CalMax(node);
node = node->p;
}
}
template<class T>
T FindMax(T x,T y)
{
if (x>y)
return x;
else
return y;
}
template<class T>
RBSearchTree<T>::CalMax(RBTreeNode<T> *node)
{
T num1 = node->i->high;
T num2 = node->left->max;
T num3 = node->right->max;
if (node->left == NILNode)
num2 = num1-1;
if (node->right == NILNode)
num3 = num1-1;
node->max = FindMax(FindMax(num1,num2),num3);
}
int main()
{
Interval<int> *a[10] = {
new Interval<int>(16,21),
new Interval<int>(8,9),
new Interval<int>(5,8),
new Interval<int>(15,23),
new Interval<int>(0,3),
new Interval<int>(6,10),
new Interval<int>(26,26),
new Interval<int>(25,30),
new Interval<int>(17,19),
new Interval<int>(19,20),
};
RBSearchTree<int> *tr = new RBSearchTree<int>(a,10);
tr->MidWalk();
RBTreeNode<int> *node = tr->Search(new Interval<int>(22,25));
cout<<"["<<node->i->low<<","<<node->i->high<<"]"<<endl;
node = tr->Search(new Interval<int>(11,14));
cout<<"["<<node->i->low<<","<<node->i->high<<"]"<<endl;
tr->Delete(new Interval<int>(6,10));
tr->MidWalk();
}
运行结果如下
我在不同的电脑上运行,有时候会得到下面的结果

上述结果是一样的,不过下面的图是用16进制表达的(不信你可以自己算算看,14是16+4=20),出现上述两种结果的原因不详,运行环境实在CodeBlock
补充:
1、红黑树的创建规则改变为, i.low小的放在left,i.low大的放在右节点
2、封装了一个计算max的方法CalMax(RBTreeNode *node)
3、对原有的Search方法进行更改,规则改为:如果i.low≤i’.high且i.high≥i’.high,则i和i’重叠,返回i’。i为搜索的区间,i’为搜索树中节点的区间。
1、2两点比较好理解,就不进行说明了,这里主要说一下第3点。
①while(node !=NILNode && (i->low > node->i->high || i->high < node->i->low)),这个循环条件很清晰,就是说明了两件事:从根节点找到叶节点(NILNode);整个过程中都没有重叠节点
②if (node->left != NILNode && node->left->max >= i->low),这个条件判断的是当左节点存在,并且left.max≥i.low的时候,从左子树中搜索重合点,否则从右节点搜索。
(1)我们首先判断 右节点的条件,也就是 node = node->right 的情况:
无论左节点是否为NILNode节点,当node->left->max >= i->low 不满足的时候,即node->left->max < i->low,此时已经违背了重叠的原则 “i.low≤i’.high且i.high≥i’.high”,所以如果存在重叠节点,只能在右节点中,如下图(a)。
(2)接着我们来判断左节点的条件,也就是 node = node->left 的情况:
因为 node->left->max >= i->low ,所以左子树中一定存在区间i’满足
i->low ≤ node->left.max = i’->high 如下图(b)所示。此时如果左子树中找不到重叠区间,右子树中一定不存在重叠节点,因为右节点的 i’->low一定大于i.high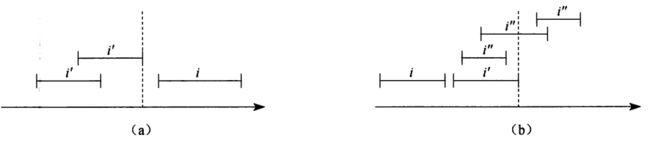
区间树在DDM区域匹配中的应用