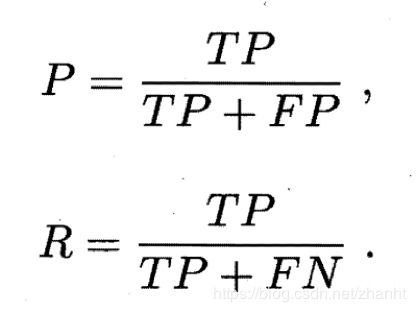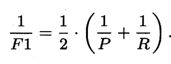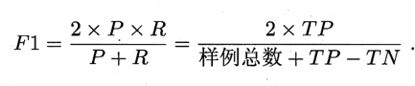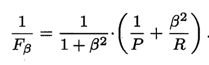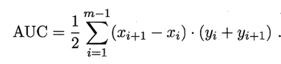模型评估指标：P-R曲线和ROC曲线

在机器学习建模中，模型评估指标用于评估不同模型的优劣。

在分类任务中，最简单的评估指标莫过于错误率和精度了，错误率表示的是错误分类的样本个数占总样本个数的比例，精度则是1减去错误率。

错误率和精度的优点是：它们不仅仅适用于二分类问题，也同样适用于多分类问题。

但是单单看错误率和精度两个指标无法很好的对模型进行合适的评估。一方面，现在不少的模型最终都是预测一个类别的概率值，为了计算错误率和精度，得设定一个阈值，以便确定预测的正例和反例。这样相当于引入了一个新的超参数，会增加复杂性和不确定行。

另一方面，以周志华老师在《机器学习》[1]书中的西瓜为例，我们挑选西瓜往往关注的不是有多少比例的西瓜判断错了，而是关注：我挑选的瓜有多少比例是好瓜，或者有多少比例的好瓜被我挑选出来了。错误率和精度无法评估这方面的比例。

准确率（Precision）和召回率（Recall），以及真正率（Ture Positive Rate）和假正率（False Positive Rate）更加的适合用于模型的评估。

本篇博文首先介绍各种指标的数学公式和基本含义，然后介绍P-R曲线和ROC曲线，最后分析两者的联系和差异，以及如何选择。

 

一：基本定义

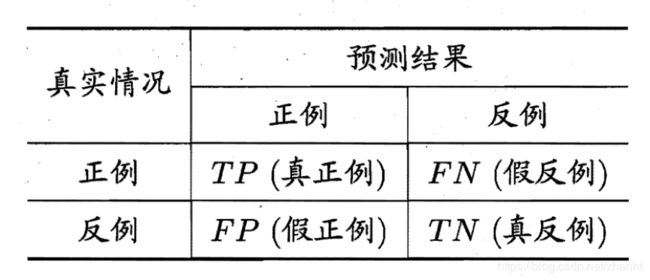
对于二分类问题，样本点的实际类别和预测的类别两辆组合，会产生4种情况：(1)实际为正，预测为正；(2)实际为正，预测为负；(3)实际为负，预测为正；(4)实际为负，预测为负。四种情况，可以组成如下的混淆矩阵（Confusion Matrix）。

                                 

然后，准确率P和召回率R定义如下：

准确率表示的是，预测为正例的样本中，有多少比例是预测对的。对应前面例子，类似挑的瓜里面多少比例是好瓜。

召回率表示的是，真实为正例的样本中，有多少比例被预测对了。类似，好瓜有多少比例被我挑中了。

一般会综合考虑P和R，定义两者的调和平均值为F1。表示如下：

调和平均相比较于算数平均，更加重视较小值。也可以给P和R加上权重，表示如下：

更加重视准确率，就意味着“宁缺毋滥”，适用于对精度要求高的场景，如商品推荐。

而重视召回率，意味着“宁可错杀一百，不能放过一个”，适用于类似反欺诈等场景。

真正率（TPR）和假正率（FPR）定义如下：

TPR表示的是，正例的样本被正确预测为正例的比例。

FPR表示的是，反例的样本中被错误预测为正例的比例。

 

二：P-R曲线和ROC曲线

将样本按照按照预测为正例的概率值从大到小进行排序，从第一个开始，逐个将当前样本点的预测值设置为阈值，有了阈值之后，即可得出混淆矩阵各项的数值，然后计算出P和R，以R为横坐标，P为纵坐标，绘制于图中，即可得出P-R曲线，示意图如下。

                                         

当一个模型a的P-R曲线完全包住另一个模型b的P-R曲线时，即可认为a优于b。其他情况下，可以使用平衡点，也即F1值，或者曲线下的面积来评估模型的好坏。

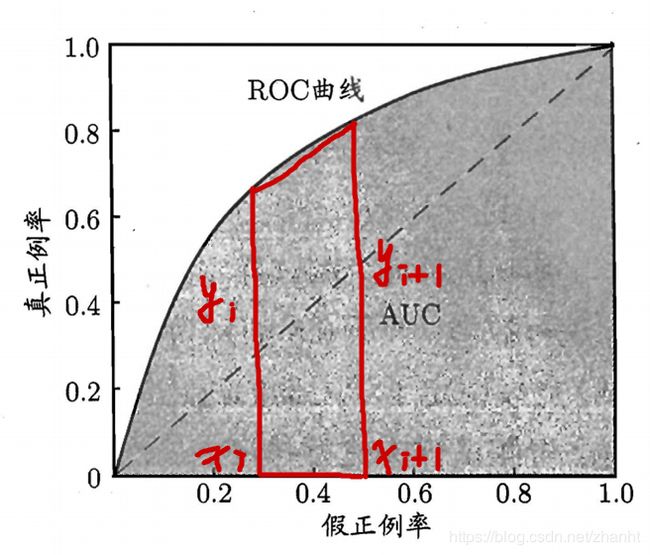
类似的，将样本排好序后，从第一个开始，逐渐的将其和其之前的点预测为正例，其他的预测为反例，这样就能计算出TPR和FPR，以FPR为横坐标，TPR为纵坐标，即可绘制出ROC（Receiver Operating Characteristic）曲线，示意图如下。ROC曲线下面覆盖的面积称为AUC（Area Under ROC Curve）。用于评估模型的好坏，面积的计算可以通过梯形去插值计算，公式和示意图如下：

                                           

 

三：两者的联系

P-R曲线和ROC曲线都能对模型进行评估，两个曲线也自然有着千丝万缕的联系。

文章[2]中就提出了几个论点并且进行了证明，这里进行简单描述下。

• 当召回率不等于0时，P-R曲线的点和ROC曲线的点都能一一对应。

原因也很简单，两个曲线的点都能对应一个数值确定的混淆矩阵，当召回率不为0时，可以通过P和R的数值，加上样本中正例和反例的个数组方程组，便可计算出混淆矩阵中各项的数值，进而计算真正率和假正率，这样，ROC对应的点也就找到了。

• 当一个模型a在P-R上优于b时，a在ROC曲线上也同样会优于b，反过来也同样成立。

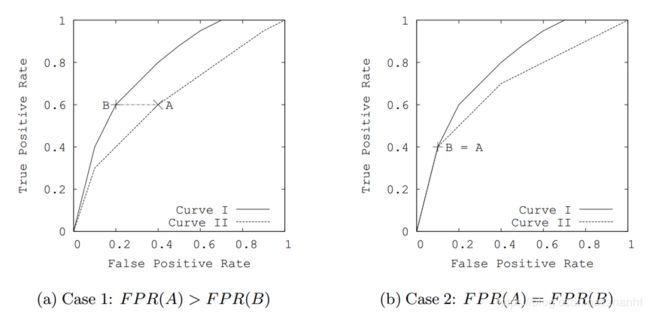
证明如下，假定算法1优于算法2。先证明ROC => P-R，固定TPR画条平行横轴的直线，直线和算法1交于点B，和算法2交于点A。示意图如下：

两个点的TPR相等，结合TPR的定义可以得出两者的TP相等，因为算法1优于2，所以B点的FPR小于等于A点的FPR，根据FPR定义，可以得出FP1 <= FP2，最后根据准确率P的定义可以得出，P1 >= P2。两点的TPR相等，也即两点的P-R曲线中，横坐标召回率相等，P1 >= P2，即可得出算法1在P-R曲线中也优于算法2。

反方向的证明思路一样，通过固定召回率，这里就不证明了。

 

四：两者的区别，如何选择

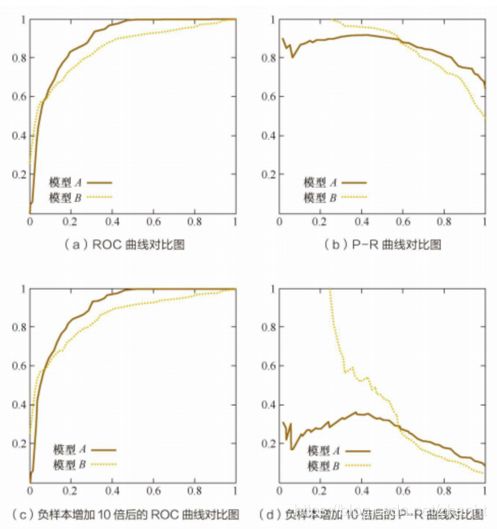
一般情况下，两者都能很好的完成模型的评估工作，效果相差也不大。但是，当正样本个数严重小于负样本个数，收据严重倾斜时，P-R曲线相比较于ROC曲线更加适合[3]。P-R曲线能够更加的明显直观的表现出模型之间的好坏，示意图如下[4]：

                                            

观察图能够发现，当正样本比例减小时，ROC曲线变化不明显，但是P-R曲线的纵坐标，即准确率出现了明显的衰减。

原因是，当样本严重倾斜时，我们假定召回率不变，那么表现较差的模型必然会召回更多的负样本，那么FP(假正例)就会迅速增加，准确率就会大幅衰减。

下面通过简单的数据直观的表示，假设样本总数10万个，正样本100个，负样本99900个。算法1召回了100个样本，90个为正样本。算法2召回了200个样本，90个正样本。通过上面的公式能计算出：

P(algo1) = 0.9, R(algo1) = 0.9, TPR(algo1) = 0.9, FPR(algo1) = 0.0001

P(algo2) = 0.45, R(algo2) = 0.9, TPR(algo2) = 0.9, FPR(algo2) = 0.001

diff(P) = 0.45, 但是diff(FPR)=0.0009。因此P-R曲线能够更加直观的表现两个算法的差异。

 

五：结论

通过上面的分析，我相信大家对P-R曲线，和ROC曲线都有了深入的理解。

我们可以得出如下结论：一般情况下，模型评估选择P-R或者ROC没啥区别，但是当正样本的个数严重少于负样本个数时，P-R曲线相比较于ROC曲线能够更加直观的表现模型之间的差异，更加合适。

 

参考文献：

[1] 机器学习 - 周志华

[2] The Relationship Between Precision-Recall and ROC Curves. - Jesse Davis

[3] What is the difference between a ROC curve and a precision-recall curve? When should I use each? – Quora

[4] P-R曲线及与ROC曲线区别. – 光彩照人(博客园)