OFDM Introduction
OFDM Introduction
- Overview
- Cyclic Prefix
- Example
Overview
OFDM代表 Orthogonal Frequency Division Multiplexing(正交频分复用)。 如果您理解以下关键字的含义,那么您将对OFDM有不错的大体理解。
• Orthogonal(正交)
• Frequency Division(分频)
• Multiplexing(复用)
在浏览本页时,您将会了解这些所有术语的含义。
OFDM是一种将一个宽频带分割成许多小频带(frequencies)(我们称这种分割频带为子载波)的技术,并将数据传送到这些子载波中的每一个子载波上,如下所示。换句话说,我们把一个宽频带分成多个小/窄频率。这就是“分频”的意思;由于这些子载波上的所有数据都是同时传输的,我们可以说这是一种“多路复用”。
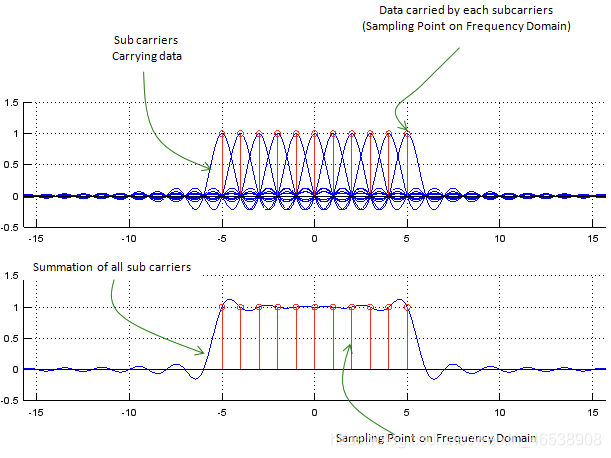
现在您可能会对此有疑问。 我们可以为每个子载波(子载波,分频)设置多小? 例如,如果有1 Mhz带宽作为全带宽,我们可以分成多少个子载波? 如果将其以1 Khz为间隔可以分为1000个子载波并在每个子载波上携带一位,则可以同时发送1000位。 如果将其以10 Khz的间隔分为100个子载波,并在每个子载波上携带一位,则一次可以发送100位。
您会选择哪个? 你肯定想把它分成1000个子载波。您甚至会说我想将其拆分为更多的子载波。
但是不幸的是,不能把子载波的间隔分的过小。 如果将其分为太多的子载波,并且子载波之间的空间太小,则相邻子载波之间的干扰很可能将非常高。 但是,如果您将每个子载波的间隔分的很大随之子载波数量少,则子载波之间的干扰会少很多。但是那样的话,数据速率会降低。
作为一种优化方案,OFDM按照如下所示将频带划分为多个子载波。 在下图频域中的每个采样点上,只有一个载波的值不为零,所有其他子载波在该采样点处的值为零。 这意味着即使存在多个子载波,它们都是相互独立的且不影响其他子载波,此特性被称为“正交’’。 (如果两个函数或矢量是正交的,则意味着它们彼此是线性独立的。您可以从WiKi中找到正交性的数学定义,但是从中找出正交性的实际含义并不容易。简单地说,“正交”表示“独立”,“独立”表示“无交互/干扰”。因此“正交”表示“无干扰”)
采样值位于和曲线的正上方
如果在原始采样点采样,则保留与原始值相同的值
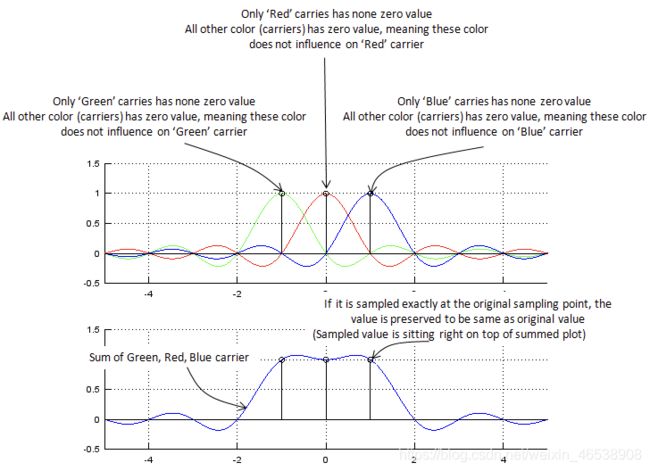
OFDM是一种很好的合理利用给定频率的方法。但是这种方法有一个缺点。 为了使该方法有效地工作,子载波之间的间隔要精确地保持在指定的位置上满足正交性。
如果子载波之间的空间无法准确维护并且四处漂移,会怎么办。 下面显示了这种情况的一个示例。 当分别绘制每个子载波(上图)时,您不会看到很大的差异。但是当所有这些子载波被汇总在一起时,您会注意到这些差异,如下图所示。
不幸的是,实际上不存在没有频率漂移的环境。 因此,在设计OFDM时,首先必须确定系统能够容忍由于子载波的频率漂移而导致信号失真的频率空间。(引起子载波频率漂移的最常见原因是“衰落”和“多普勒效应”)。

为了让您对OFDM的概念和频率漂移的影响有点兴趣,我放置了用于创建上面所示曲线的Matlab / Octave源代码。 尝试对NoOfCarriers和fnoiseMax配置不同的值,并观察结果如何不同。
NoOfCarriers = 11; % Put an Odd Number
f = -5pi:pi/50:5pi;
fnoiseMax = 0.3;
iMin = -(NoOfCarriers-1)/2;
iMax = (NoOfCarriers-1)/2;
csum = zeros(1,length(f));
close all;
fList = [];
cList = [];
subplot(2,1,1);
hold on;
for i=iMin:1:iMax,
fnoise = fnoiseMax*(rand()-0.5);
fshift = (i .* (1/pi) .* pi) .+ fnoise;
c = sinc(f .- fshift);
csum = csum + c;
fList = [fList,fshift];
cList = [cList,max©];
plot(f,c);axis([min(f),max(f),-0.5,1.5]);
stem((i * (1/pi) * pi) + fnoise,1,‘r-’);
end;
grid();
hold off;
subplot(2,1,2);
hold on;
plot(f,csum);grid();axis([min(f),max(f),-0.5,1.5]);
stem(fList,cList,‘r-’);
hold off;
Cyclic Prefix
现在让我们看一下时域中的信号。 以下是依次显示两个OFDM符号的插图。
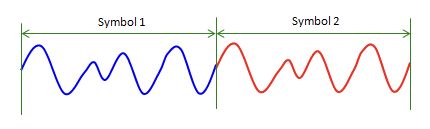
在理想情况下,该信号没有问题,但是如果第一个符号延迟一点会发生什么。 在这种情况下,第一个符号的结尾部分将溢出到下一个符号时间中,并干扰下一个符号,如下所示。 不同符号之间的这种干扰称为“符号间干扰(ISI:Inter Symbol Interference)”。
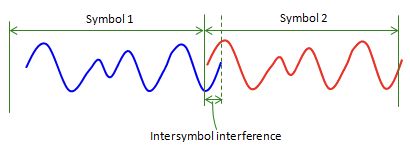
解决这个问题的办法是什么? 您可能想要防止信号延迟。 但这是不可能的,因为我们无法控制无线电信道本身(物理介质本身)。 因此,唯一的方法是设计我们的系统来处理这种情况。 一个简单的解决方案是在符号之间留出一定的时间间隔,以使一个符号即使延迟也不会溢出到下一个符号中。

有了这个间隙,系统将在一定程度上能够容忍延迟和符号间干扰的问题。但是存在实际问题。 问题是“间隔中该填补什么?”。 什么也不放(例如关闭传输)会好吗? 如果在间隙期间完全关闭信号,则可能导致放大器出现问题。 为减少此问题,我们从末端复制一部分信号并将其粘贴到此间隙中。 此复制的部分放在开头被称为“CP循环前缀”。
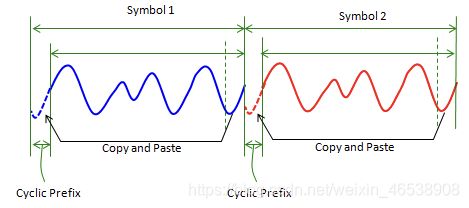
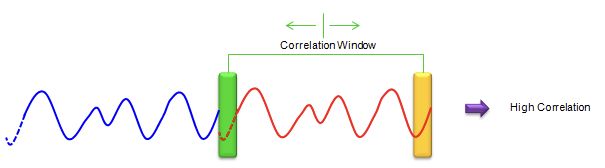
正如我所解释的那样,循环前缀的主要目的是减少ISI(符号间干扰)。但是通过复制原始符号的结尾部分的数据来生成循环前缀,还可以获得额外的优势。 它有助于找到符号边界(符号的开始和结束)。 就像这样:采取一个具有循环前缀长度的样本(窗口)的序列。 然后从除第一个序列外(符号长度-CP长度)取出另一个序列,该序列与第一个序列具有相同的长度。 之后计算两个序列的相关性。 如果两个序列与符号的开始和结尾完全对齐,则它们的相关性将非常高。因为两个序列中的内容几乎相同。
如果两个序列(两个窗口)与符号边界(符号的开始和结束)不对齐,则相关性不会很高,如下所示。
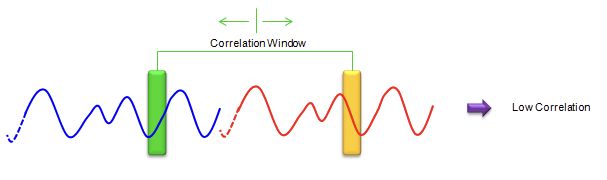
如果您上下滑动这两个窗口,并找到相关度最高的位置,那就是slot边界(这里不是符号的边界)。
Example
我希望您通过一节的学习能够对OFDM工作原理有一个大致的了解。但这只是一个概念性的描述,在概念和实际实现之间的细节填充会有些差距。 让我给您一个示例,该示例将为您提供比先前概念更具体的想法。 此示例的总体思想基于IEEE 802.11(WLAN规范),但此示例也缺少很多细节。 但是,它将为您提供有关OFDM实现的更具体的想法。
假设您获得了如下的OFDM规范。 (在大多数情况下,规范不会以这种插图的形式给出,但(以我的建议)以图形形式描述规范会有所帮助)。
在OFDM实现中,精确中心处的频率(frequence)不携带任何子载波。并且在频谱的两端有一定数量的子载波不具有任何信息子载波。 该区域称为保护频带,主要是为了减少对相邻频带的干扰。
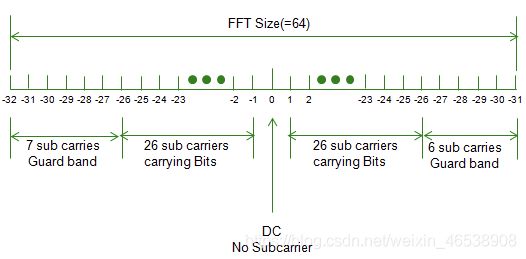
说明:上图的右侧的-23,-24,-25,-26.。。。应该是正数:23,24,25,26.。。。
现在,让我们按照以下步骤从要发送的位数据中实现OFDM信号。 为简单起见,我们使用的调制是BPSK,每个星座点承载一位。 根据给定的规范,在分配给频带的64个子载波中,只有52个子载波是可以携带数据的子载波,如下所示。
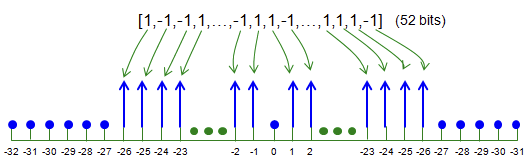
对于此步骤,首先我们必须生成一个比特序列,该比特序列将由一个OFDM符号承载。 您可以按照以下方式生成随机位序列。(在真实通信中,没有人会使用随机数据进行传输。如果是真实通信,则该数据将是文档文件,音乐或电影等,但在模拟情况下,我们通常使用随机数据)。
![]()
下一步是将用户数据映射到能携带数据的子载波。 实现如下。 (乍一看,除非您对Matlab / Octave数组操作非常熟悉,否则对您来说不是特别详细。您可以使用for循环来执行此操作,但是遵循以下方法会更简单)。

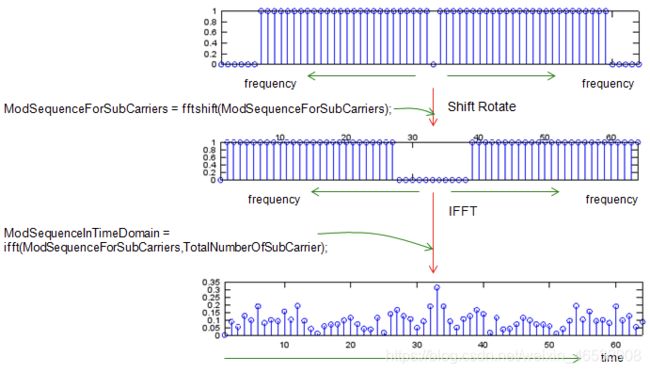
通过上述过程,我们在频域中将比特流分配给了子载波。 但是所有通信(数据发送和接收)都发生在时域中。 因此,我们必须将频域数据转换为时域序列,如下所示。 您已经知道IFFT(快速傅立叶逆变换)是将频域数据转换为时域数据的工具。
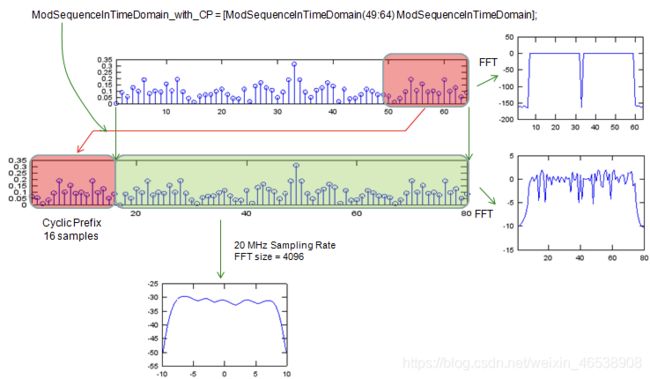
下一步是将循环前缀添加到上一步中获得的时域数据中。 循环前缀的生成非常简单,它是从结尾部分直接复制一部分数据,并把该COPY数据放置在数据序列的开头。
下一步是在上一步得到的时域数据中添加循环前缀。循环前缀的生成非常简单,它是从数据的末尾直接复制部分数据,并将副本放在数据序列的开头。
以下是Matlab / Octave代码,以实现上述所有步骤。
TotalNumberOfSubCarrier = 64;
% for each symbol bits a1 to a52 are assigned to subcarrier
% index [-26 to -1 1 to 26]
subcarrierIndex_Data = [-26:-1 1:26];
BitsPerSymbol = 52;
close all;
figure;
% BPSK modulation
ModSequence = 2*randi([0 1],1,BitsPerSymbol)-1;
subplot(6,1,1); stem(abs(ModSequence));xlim([1 length(ModSequence)]);
TimeDomainSequence = []; % empty vector
ModSequenceForSubCarriers = zeros(1,TotalNumberOfSubCarrier);
% assigning bits a1 to a52 to subcarriers [-26 to -1, 1 to 26]
ModSequenceForSubCarriers(subcarrierIndex_Data+TotalNumberOfSubCarrier/2+1) = ModSequence(1,:);
subplot(6,1,2); stem(abs(ModSequenceForSubCarriers));xlim([1 length(ModSequenceForSubCarriers)]);
% shift subcarriers at indices [-26 to -1] to fft input indices [38 to 63]
ModSequenceForSubCarriers = fftshift(ModSequenceForSubCarriers);
subplot(6,1,3); stem(abs(ModSequenceForSubCarriers));xlim([1 length(ModSequenceForSubCarriers)]);
ModSequenceInTimeDomain = ifft(ModSequenceForSubCarriers,TotalNumberOfSubCarrier);
subplot(6,1,4); stem(abs(ModSequenceInTimeDomain));xlim([1 length(ModSequenceInTimeDomain)]);
% adding cyclic prefix of 16 samples
ModSequenceInTimeDomain_with_CP = [ModSequenceInTimeDomain(49:64) ModSequenceInTimeDomain];
subplot(6,1,5); stem(abs(ModSequenceInTimeDomain_with_CP));
xlim([1 length(ModSequenceInTimeDomain_with_CP)]);
TimeDomainSequence = [TimeDomainSequence ModSequenceInTimeDomain_with_CP];
subplot(6,1,6); stem(abs(TimeDomainSequence));xlim([1 length(TimeDomainSequence)]);
figure;
SamplingRate = 20;
[PowerSpectrum,W] = pwelch(TimeDomainSequence,[],[],4096,20);
subplot(1,3,1);plot([-2048:2047]SamplingRate/4096,10log10(fftshift(PowerSpectrum)));
xlabel(‘frequency, MHz’)
ylabel(‘power spectral density’)
subplot(1,3,2);plot(10log10(fftshift(abs(fft(ModSequenceInTimeDomain)))));
xlim([1 length(ModSequenceInTimeDomain)]);
subplot(1,3,3);plot(10log10(fftshift(abs(fft(TimeDomainSequence)))));
xlim([1 length(TimeDomainSequence)]);
备注:以上文章参考的是sharetechnote中相关文档