李宏毅机器学习作业二Classification：年收入分类

1作业任务

二元分类是机器学习中最基础的问题之一，在这份教学中，你将学会如何实作一个线性二元分类器，来根据人们的个人资料，判断其年收入是否高于50000美元。我们将以两种方法：logistic regression与generative model，来达成以上目的，你可以尝试了解、分析两者的设计理念及差别。

2原始代码

导入数据集

X_train_fpath = './data/X_train'
Y_train_fpath = './data/Y_train'
X_test_fpath = './data/X_test'
output_fpath = './output_{}.csv'

with open(X_train_fpath) as f:
    next(f)
    X_train = np.array([line.strip('\n').split(',')[1:] for line in f], dtype=float)
with open(Y_train_fpath) as f:
    next(f)
    Y_train = np.array([line.strip('\n').split(',')[1] for line in f], dtype=float)
with open(X_test_fpath) as f:
    next(f)
    X_test = np.array([line.strip('\n').split(',')[1:] for line in f], dtype=float)

标准化

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。这里使用的是StandardScaler，x =(x - )/。

标准化函数_normalize()

• train：bool变量，标识是否为测试集
• specified_column：需要被标准化的列，如果为None，则所有列均需要被标准化
• X_mean：均值
• X_std：方差

def _normalize(X, train=True, specified_column=None, X_mean=None, X_std=None):
    # is比较的是两个变量的地址，而==比较的是两个变量的值，当一个类重写了__eq__()方法，那么==的判断就会有问题了。
    if specified_column is None:
        specified_column = np.arange(X.shape[1])
    if train:
        X_mean = np.mean(X[:, specified_column], 0).reshape(1, -1)
        X_std = np.std(X[:, specified_column], 0).reshape(1, -1)

    X[:, specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8)
    return X, X_mean, X_std

分割测试集和验证集

training set：训练集是用来训练模型的。遵循训练集大，开发，测试集小的特点，占了所有数据的绝大部分。
development set：用来对训练集训练出来的模型进行测试，通过测试结果来不断地优化模型。
test set：在训练结束后，对训练出的模型进行一次最终的评估所用的数据集。

将训练集和验证集的数据按照(1 - dev_ratio)/dev_ratio的比例进行切分

X_train, Y_train, X_dev, Y_dev = _train_dev_split(X_train, Y_train, dev_ratio=dev_ratio)、

def _train_dev_split(X, Y, dev_ratio=0.25):
    train_size = int(len(X) * (1 - dev_ratio))
    return X[:train_size], Y[:train_size], X[train_size:], Y[train_size:]

一些有用的函数

• _shuffle(X, Y)：将X和Y列与列之间的顺序打乱。

def _shuffle(X, Y):
    randomsize = np.arange(len(X))
    np.random.shuffle(randomsize)
    return X[randomsize], Y[randomsize]

• _sigmoid(z)：sigmoid函数，np.clip()函数将数组中的值限制在1e-8~1-1e-8

def _sigmoid(z):
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - 1e-8)

• _f(W, x, b)：实现了$f(x)=\sigma \left(\sum w_i\ast x_i+b\right)$

def _f(W, x, b):
    return _sigmoid(np.matmul(W, x) + b)

• _predict(X, w, b)：通过f(x)计算出来的值在0-1之间，通过四舍五入即可得到预测的结果。

def _predict(X, w, b):
    return np.round(_f(X, w, b)).astype(np.int)

• _accuracy(Y_pred, Y_label)：计算Y_pred与Y_label的差距，当Y_pred与Y_label异号时矩阵中那一行的结果为1，最后取平均值即为错误率，1-错误率就是正确率了。

def _accuracy(Y_pred, Y_label):
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc

Logistic Regression

第n个数据为$(x^n,{\hat{y}}^n)$，${\hat{y}}^n$的真值为0、1。

预测值$y^n=f_w{,}_b(x)=\sigma (\sum _i{w}_i{x}_i+b)=\frac{1}{1+e^{-\left(\sum _i{w}_i{x}_i+b\right)}}$

损失函数（Loss Function）

$L(w,b)=f_w{,}_b(x^1)f_w{,}_b(x^2)(1-f_w{,}_b(x^3))\cdots f_w{,}_b(x)$

$w^{\ast },b^{\ast }=\arg \underset{w,b}{\max }L(w,b)=\arg \underset{w,b}{\min }(-\ln L(w,b))$

$-\ln L(w,b)=-\ln f_w{,}_b(x^1)-\ln f_w{,}_b(x^2)-\ln (1-f_w{,}_b(x^3))-\cdots =\sum _n-[{\hat{y}}^n\ln f_w{,}_b(x^n)+(1-{\hat{y}}^n)\ln (1-f_w{,}_b(x^n))]$

def _cross_entropy_loss(y_pred, Y_label):
    # 为什么最后是一个标量？
    cross_entropy = -np.dot(Y_label, np.log(y_pred)) - np.dot((1 - Y_label), np.log(1 - y_pred))
    return cross_entropy

梯度

推导过程省略，详情见博客：https://blog.csdn.net/iteapoy/article/details/105477848

$\frac{\partial (-\ln L(w,b))}{\partial w_i}=-\sum _n({\hat{y}}^n-fw,b(x^n))x_i^n$

$\frac{\partial (-\ln L(w,b))}{\partial b}=-\sum _n({\hat{y}}^n-fw,b(x^n))$
最后更新的公式为
$$\begin{gathered} w_i=w_i-\eta (-\sum _n({\hat{y}}^n-fw,b(x^n))x_i^n) \\ {b}_i=b_i-\eta (-\sum _n({\hat{y}}^n-fw,b(x^n))) \end{gathered}$$
此处pred_error是长度为8的一个ndarray对象，而X.T的维度是5108，当为array的时候，默认df就是对应元素的乘积，multiply也是对应元素的乘积，dot（d,f）会转化为矩阵的乘积， dot点乘意味着相加，而multiply只是对应元素相乘，不相加。最后得到的维度也是510*8。

numpy 数组和矩阵的乘法的理解：https://blog.csdn.net/bbbeoy/article/details/72576863

def _gradient(X, Y_label, w, b):
    y_pred = _f(X, w, b) # m * 1
    pred_error = Y_label - y_pred # m * 1
    # 此处的1表示维度，X的维度是m * n
    w_grad = -np.sum(pred_error * X.T, 1)
    b_grad = -np.sum(pred_error)
    return w_grad, b_grad

训练

我们使用小批次梯度下降法(mini-batch)来训练。训练数据被分为许多小批次，针对每一个小批次，我们分别计算其梯度以及损失，并根据该批次来更新模型的参数。当一次循环完成，也就是整个训练集的所有小批次都被使用过一次以后，我们将所有训练数据打散并且重新分成新的小批次，进行下一个循环，直到事先设定的循环数量达成为止。

w = np.zeros((data_dim,))
b = np.zeros((1,))
max_iter = 10
batch_size = 8
learning_rate = 0.2
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []
step = 1

for epoch in range(max_iter):
    X_train, Y_train = _shuffle(X_train, Y_train)
    for idx in range(int(np.floor(train_size / batch_size))):
        X = X_train[idx * batch_size:(idx + 1) * batch_size]
        Y = Y_train[idx * batch_size:(idx + 1) * batch_size]
        w_grad, b_grad = _gradient(X, Y, w, b)
        w = w - learning_rate / np.sqrt(step) * w_grad
        b = b - learning_rate / np.sqrt(step) * b_grad
        step += 1
    y_train_pred = _f(X_train, w, b)
    Y_train_pred = np.round(y_train_pred)
    train_acc.append(_accuracy(Y_train_pred, Y_train))
    train_loss.append(_cross_entropy_loss(y_train_pred, Y_train) / train_size)

    y_dev_pred = _f(X_dev, w, b)
    Y_dev_pred = np.round(y_dev_pred)
    dev_acc.append(_accuracy(Y_dev_pred, Y_dev))
    dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev) / dev_size)
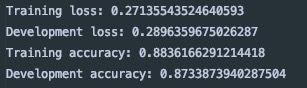
print('Training loss: {}'.format(train_loss[-1]))
print('Development loss: {}'.format(dev_loss[-1]))
print('Training accuracy: {}'.format(train_acc[-1]))
print('Development accuracy: {}'.format(dev_acc[-1]))

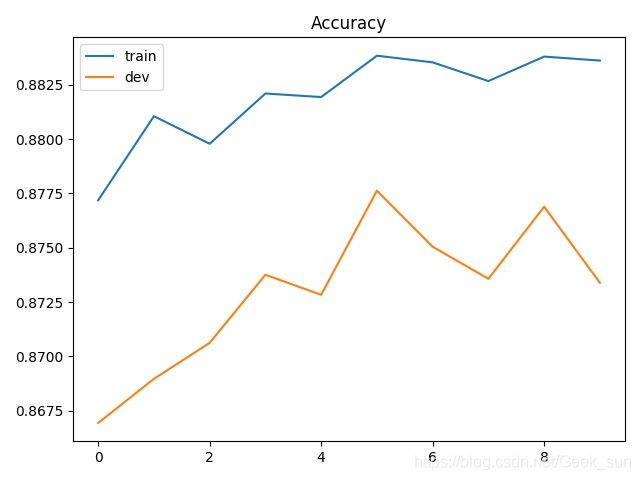
画出准确率和损失曲线

预测测试集

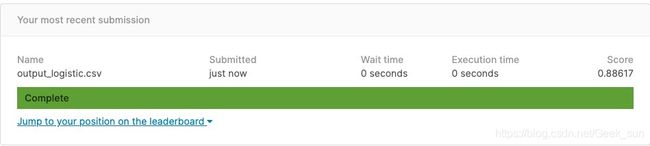
predictions = _predict(X_test, w, b)
with open(output_fpath.format('logistic'), 'w') as f:
    f.write('id,label\n')
    for i, label in enumerate(predictions):
        f.write('{},{}\n'.format(i, label))