OpenCV--直线拟合fitLine及求两直线对称轴

直线拟合fitLine

void cv::fitLine(  
    cv::InputArray points, // 二维点的数组或vector  
    cv::OutputArray line, // 输出直线,Vec4f (2d)或Vec6f (3d)的vector  
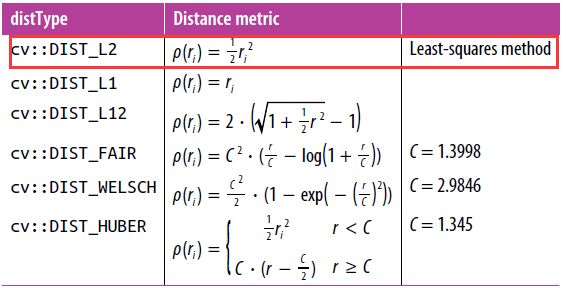
    int distType, // 距离类型  
    double param, // 距离参数  
    double reps, // 径向的精度参数  表示直线到原点距离的精度，建议取 0.01。设为0，则自动选用最优值
    double aeps // 角度精度参数  表示直线角度的精度，建议取 0.01
); 

◆输出line：为一个四元素的容器，如Vec4f - (vx, vy, x0, y0)。(vx, vy) 是直线的方向向量，(x0, y0) 是直线上一点。
画出直线用cv::line(image, point1, point2, cv::Scalar(0, 255, 0), 2, 8, 0);需要输入直线上的两个点，

    double cos_theta = line[0];
    double sin_theta = line[1];
    double x0 = line[2], y0 = line[3];

    double k = sin_theta / cos_theta;
    double b = y0 - k * x0;
    //求出直线上另一点
    double x = 0; 
    double y = k * x + b;

    cv::line(image, Point(x0,y0), Point(x,y), cv::Scalar(255), 1);

◆参数param含义如下，为0时自动选择最优值

Numerical parameter ( C ) for some types of distances. If it is 0, an optimal value is chosen.

◆距离类型distType一共有六种，如下图，其中CV_DIST_L2就是最小二乘法

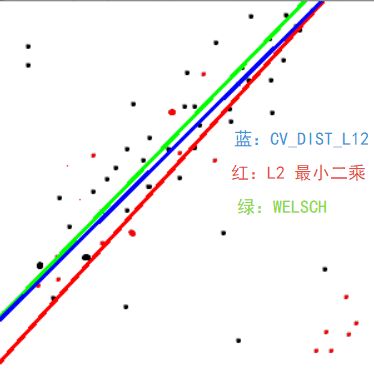
最小二乘法抗干扰能力不如其它5种方法，实验代码见附1

原图

拟合结果

求两直线对称轴

由直线拟合得到两条Vec4f类型直线，求其对称轴
（1）求两直线交点

/*函数功能：求两条直线交点*/
/*输入：两条Vec4f类型直线
 *  Vec4f - (vx, vy, x0, y0)
 * (vx, vy) 是直线的方向向量，(x0, y0) 是直线上一点*/
/*返回：Point2f类型的点*/
Point2f getCrossPoint(Vec4f LineA, Vec4f LineB)
{

    double ka, kb;
    ka = LineA[1]/LineA[0]; //求出LineA斜率
    kb = LineB[1]/LineB[0];; //求出LineB斜率

    Point2f crossPoint;
    crossPoint.x = (ka*LineA[2] - LineA[3] - kb*LineB[2] + LineB[3]) / (ka - kb);
    crossPoint.y = (ka*kb*(LineA[2] - LineB[2]) + ka*LineB[3] - kb*LineA[3]) / (ka - kb);
    return crossPoint;
}

（2）对称轴斜率k2=(k0+k1)/2
（3）得到对称轴点斜式方程，令x=0代入，求得直线上另一点

 double k_line2 =(k_line0+k_line1)/2;
 Point p2_1(0, k_line2*(0 - crossPoint.x) + crossPoint.y);  //x=0,求出直线上另一点
 line(drawing, p2_1, crossPoint, Scalar(0, 0, 255), 3); 	//显示拟合出的直线

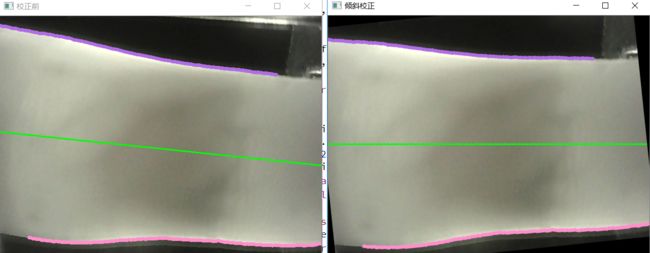
倾斜校正

Point2f center=Point2f(src.rows/2,src.cols/2);
Mat martix = getRotationMatrix2D(center, k_line2/CV_PI*180, 1);//得到仿射矩阵  k_line2/CV_PI*180 弧度转角度
warpAffine(src, dst, martix, drawing.size());

附1 实验代码

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include 
using namespace cv;
using namespace std;

int main()
{
	const char* filename = "1.bmp";
	Mat src_image = imread(filename, 1);
	if (src_image.empty())
	{
		cout << "Couldn't open image!" << filename;
		return 0;
	}
	int img_width = src_image.cols;
	int img_height = src_image.rows;

	Mat gray_image, bool_image;
	cvtColor(src_image, gray_image, CV_RGB2GRAY);
	threshold(gray_image, bool_image, 0, 255, CV_THRESH_OTSU);
	imshow("二值图", bool_image);
	//获取二维点集
	vector<Point> point_set;
	Point point_temp;
	for (int i = 0; i < img_height; ++i)
	{
		for (int j = 0; j < img_width; ++j)
		{
			if (bool_image.at<unsigned char>(i, j) < 255)
			{
				point_temp.x = j;
				point_temp.y = i;
				point_set.push_back(point_temp);
			}
		}
	}

	//直线拟合 	
	//拟合结果为一个四元素的容器，比如Vec4f - (vx, vy, x0, y0)
	//其中(vx, vy) 是直线的方向向量
	//(x0, y0) 是直线上的一个点
	Vec4f fitline;
	//拟合方法采用最小二乘法
	fitLine(point_set, fitline, CV_DIST_L2, 0, 0.01, 0.01);

	//求出直线上的两个点
	double k_line = fitline[1] / fitline[0];
	Point p1(0, k_line*(0 - fitline[2]) + fitline[3]);
	Point p2(img_width - 1, k_line*(img_width - 1 - fitline[2]) + fitline[3]);
	line(src_image, p1, p2, Scalar(0, 0, 255), 2); 	//显示拟合出的直线

	Vec4f fitline1;
	//拟合方法采用CV_DIST_L12  CV_DIST_WELSCH  CV_DIST_FAIR
	fitLine(point_set, fitline1, CV_DIST_WELSCH, 0, 0.01, 0.01);

	//求出直线上的两个点
	double k_line1 = fitline1[1] / fitline1[0];
	Point p11(0, k_line1*(0 - fitline1[2]) + fitline1[3]);
	Point p12(img_width - 1, k_line1*(img_width - 1 - fitline1[2]) + fitline1[3]);
	line(src_image, p11, p12, Scalar(0, 255, 0), 2);

	Vec4f fitline2;
	//拟合方法采用CV_DIST_L12  CV_DIST_WELSCH  CV_DIST_FAIR
	fitLine(point_set, fitline2, CV_DIST_L12, 0, 0.01, 0.01);

	//求出直线上的两个点
	double k_line2 = fitline2[1] / fitline2[0];
	Point p21(0, k_line2*(0 - fitline2[2]) + fitline2[3]);
	Point p22(img_width - 1, k_line2*(img_width - 1 - fitline2[2]) + fitline2[3]);
	line(src_image, p21, p22, Scalar(255, 0, 0), 2);
	//显示拟合出的直线方程
	/*char text_equation[1024];
	sprintf_s(text_equation, "y-%.2f=%.2f(x-%.2f)", fitline[3], k_line, fitline[2]);
	putText(src_image, text_equation, Point(30, 50), CV_FONT_HERSHEY_COMPLEX, 0.5, Scalar(0, 0, 255), 1, 8);*/

	imshow("原图+拟合结果", src_image);

	waitKey();
	return 0;
}