Splay伸展树&模板
伸展树操作详解
http://wenku.baidu.com/view/cc211f126edb6f1aff001f16.html?from=rec&pos=4&weight=9&lastweight=9&count=5The Magical Splay
http://wenku.baidu.com/view/a202e27931b765ce05081416.htmlBST 拓展与伸展树 (Splay) 一日通
http://wenku.baidu.com/view/f3fbe687b9d528ea81c779b6.html?from=rec&pos=4&weight=10&lastweight=10&count=5********************************************************************************我是分割线*****************************************************************************************************************
一、简介:
伸展树,或者叫自适应查找树,是一种用于保存有序集合的简单高效的数据结构。伸展树实质上是一个二叉查找树。允许查找,插入,删除,删除最小,删除最大,分割,合并等许多操作,这些操作的时间复杂度为O(logN)。由于伸展树可以适应需求序列,因此他们的性能在实际应用中更优秀。
伸展树支持所有的二叉树操作。伸展树不保证最坏情况下的时间复杂度为O(logN)。伸展树的时间复杂度边界是均摊的。尽管一个单独的操作可能很耗时,但对于一个任意的操作序列,时间复杂度可以保证为O(logN)。
二、自调整和均摊分析:
平衡查找树的一些限制:
1、平衡查找树每个节点都需要保存额外的信息。
2、难于实现,因此插入和删除操作复杂度高,且是潜在的错误点。
3、对于简单的输入,性能并没有什么提高。
平衡查找树可以考虑提高性能的地方:
1、平衡查找树在最差、平均和最坏情况下的时间复杂度在本质上是相同的。
2、对一个节点的访问,如果第二次访问的时间小于第一次访问,将是非常好的事情。
3、90-10法则。在实际情况中,90%的访问发生在10%的数据上。
4、处理好那90%的情况就很好了。
三、均摊时间边界:
在一颗二叉树中访问一个节点的时间复杂度是这个节点的深度。因此,我们可以重构树的结构,使得被经常访问的节点朝树根的方向移动。尽管这会引入额外的操作,但是经常被访问的节点被移动到了靠近根的位置,因此,对于这部分节点,我们可以很快的访问。根据上面的90-10法则,这样做可以提高性能。
为了达到上面的目的,我们需要使用一种策略──旋转到根(rotate-to-root)。具体实现如下:
旋转分为左旋和右旋,这两个是对称的。图示:
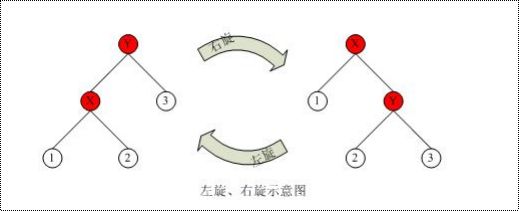
为了叙述的方便,上图的右旋叫做X绕Y右旋,左旋叫做Y绕X左旋。
下图展示了将节点3旋转到根:
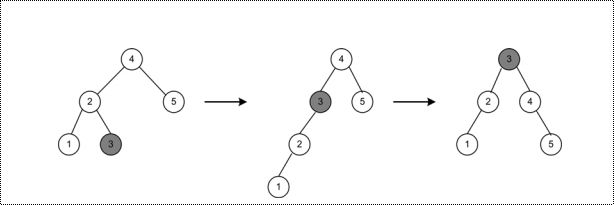
图1
首先节点3绕2左旋,然后3绕节点4右旋。
注意:所查找的数据必须符合上面的90-10法则,否则性能上不升反降!!
四、基本的自底向上伸展树:
应用伸展(splaying)技术,可以得到对数均摊边界的时间复杂度。
在旋转的时候,可以分为三种情况:
1、zig情况。
X是查找路径上我们需要旋转的一个非根节点。
如果X的父节点是根,那么我们用下图所示的方法旋转X到根:
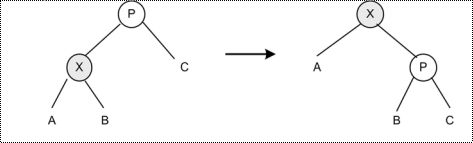
图2
这和一个普通的单旋转相同。
2、zig-zag情况。
在这种情况中,X有一个父节点P和祖父节点G(P的父节点)。X是右子节点,P是左子节点,或者反过来。这个就是双旋转。
先是X绕P左旋转,再接着X绕G右旋转。
如图所示:
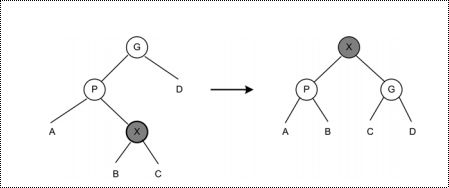
图三
3、zig-zig情况。
这和前一个旋转不同。在这种情况中,X和P都是左子节点或右子节点。
先是P绕G右旋转,接着X绕P右旋转。
如图所示:
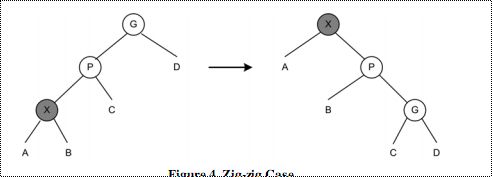
图四
下面是splay的伪代码:
P(X) : 获得X的父节点,G(X) : 获得X的祖父节点(=P(P(X)))。
Function Buttom-up-splay:
Do
If X 是 P(X) 的左子结点 Then
If G(X) 为空 Then
X 绕 P(X)右旋
Else If P(X)是G(X)的左子结点
P(X) 绕G(X)右旋
X 绕P(X)右旋
Else
X绕P(X)右旋
X绕P(X)左旋 (P(X)和上面一句的不同,是原来的G(X))
Endif
Else If X 是 P(X) 的右子结点 Then
If G(X) 为空 Then
X 绕 P(X)左旋
Else If P(X)是G(X)的右子结点
P(X) 绕G(X)左旋
X 绕P(X)左旋
Else
X绕P(X)左旋
X绕P(X)右旋 (P(X)和上面一句的不同,是原来的G(X))
Endif
Endif
While (P(X) != NULL)
EndFunction
仔细分析zig-zag,可以发现,其实zig-zag就是两次zig。因此上面的代码可以简化:
Function Buttom-up-splay:
Do
If X 是 P(X) 的左子结点 Then
If P(X)是G(X)的左子结点
P(X) 绕G(X)右旋
Endif
X 绕P(X)右旋
Else If X 是 P(X) 的右子结点 Then
If P(X)是G(X)的右子结点
P(X) 绕G(X)左旋
Endif
X 绕P(X)左旋
Endif
While (P(X) != NULL)
EndFunction
下面是一个例子,旋转节点c到根上。
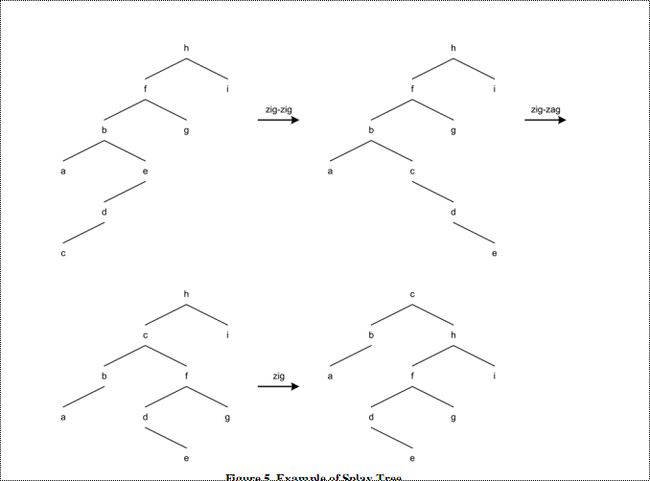
图五
五、基本伸展树操作:
1、插入:
当一个节点插入时,伸展操作将执行。因此,新插入的节点在根上。
2、查找:
如果查找成功(找到),那么由于伸展操作,被查找的节点成为树的新根。
如果查找失败(没有),那么在查找遇到NULL之前的那个节点成为新的根。也就是,如果查找的节点在树中,那么,此时根上的节点就是距离这个节点最近的节点。
3、查找最大最小:
查找之后执行伸展。
4、删除最大最小:
a)删除最小:
首先执行查找最小的操作。
这时,要删除的节点就在根上。根据二叉查找树的特点,根没有左子节点。
使用根的右子结点作为新的根,删除旧的包含最小值的根。
b)删除最大:
首先执行查找最大的操作。
删除根,并把被删除的根的左子结点作为新的根。
5、删除:
将要删除的节点移至根。
删除根,剩下两个子树L(左子树)和R(右子树)。
使用DeleteMax查找L的最大节点,此时,L的根没有右子树。
使R成为L的根的右子树。
如下图示:
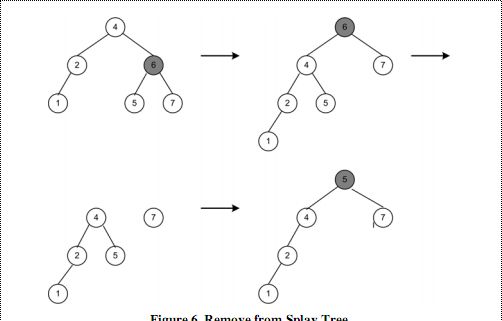
图六
六、自顶向下的伸展树:
在自底向上的伸展树中,我们需要求一个节点的父节点和祖父节点,因此这种伸展树难以实现。因此,我们可以构建自顶向下的伸展树。
当我们沿着树向下搜索某个节点X的时候,我们将搜索路径上的节点及其子树移走。我们构建两棵临时的树──左树和右树。没有被移走的节点构成的树称作中树。在伸展操作的过程中:
1、当前节点X是中树的根。
2、左树L保存小于X的节点。
3、右树R保存大于X的节点。
开始时候,X是树T的根,左右树L和R都是空的。和前面的自下而上相同,自上而下也分三种情况:
1、zig:
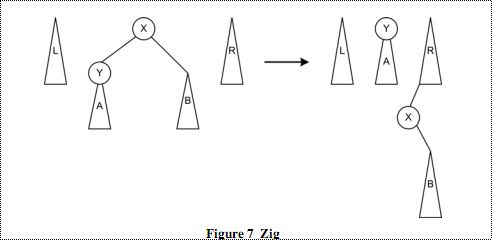
图七
如上图,在搜索到X的时候,所查找的节点比X小,将Y旋转到中树的树根。旋转之后,X及其右子树被移动到右树上。很显然,右树上的节点都大于所要查找的节点。注意X被放置在右树的最小的位置,也就是X及其子树比原先的右树中所有的节点都要小。这是由于越是在路径前面被移动到右树的节点,其值越大。读者可以分析一下树的结构,原因很简单。
2、zig-zig:
图八
在这种情况下,所查找的节点在Z的子树中,也就是,所查找的节点比X和Y都小。所以要将X,Y及其右子树都移动到右树中。首先是Y绕X右旋,然后Z绕Y右旋,最后将Z的右子树(此时Z的右子节点为Y)移动到右树中。注意右树中挂载点的位置。
3、zig-zag:

图九
在这种情况中,首先将Y右旋到根。这和Zig的情况是一样的。然后变成上图右边所示的形状。接着,对Z进行左旋,将Y及其左子树移动到左树上。这样,这种情况就被分成了两个Zig情况。这样,在编程的时候就会简化,但是操作的数目增加(相当于两次Zig情况)。
最后,在查找到节点后,将三棵树合并。如图:
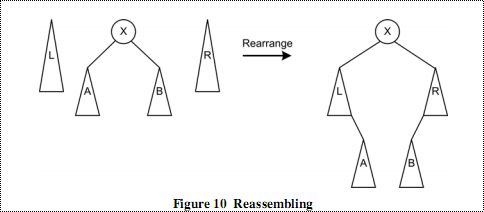
图十
将中树的左右子树分别连接到左树的右子树和右树的左子树上。将左右树作为X的左右子树。重新最成了一所查找的节点为根的树。
下面给出伪代码:
右连接:将当前根及其右子树连接到右树上。左子结点作为新根。
左连接:将当前根及其左子树连接到左树上。右子结点作为新根。
T : 当前的根节点。
Function Top-Down-Splay
Do
If X 小于 T Then
If X 等于 T 的左子结点 Then
右连接
ElseIf X 小于 T 的左子结点 Then
T的左子节点绕T右旋
右连接
Else X大于 T 的左子结点 Then
右连接
左连接
EndIf
ElseIf X大于 T Then
IF X 等于 T 的右子结点 Then
左连接
ElseIf X 大于 T 的右子结点 Then
T的右子节点绕T左旋
左连接
Else X小于 T 的右子结点‘ Then
左连接
右连接
EndIf
EndIf
While !(找到 X或遇到空节点)
组合左中右树
EndFunction
同样,上面的三种情况也可以简化:
Function Top-Down-Splay
Do
If X 小于 T Then
If X 小于 T 的左孩子 Then
T的左子节点绕T右旋
EndIf
右连接
Else If X大于 T Then
If X 大于 T 的右孩子 Then
T的右子节点绕T左旋
EndIf
左连接
EndIf
While !(找到 X或遇到空节点)
组合左中右树
EndFuntion
下面是一个查找节点19的例子:
在例子中,树中并没有节点19,最后,距离节点最近的节点18被旋转到了根作为新的根。节点20也是距离节点19最近的节点,但是节点20没有成为新根,这和节点20在原来树中的位置有关系。

这个例子是查找节点c:
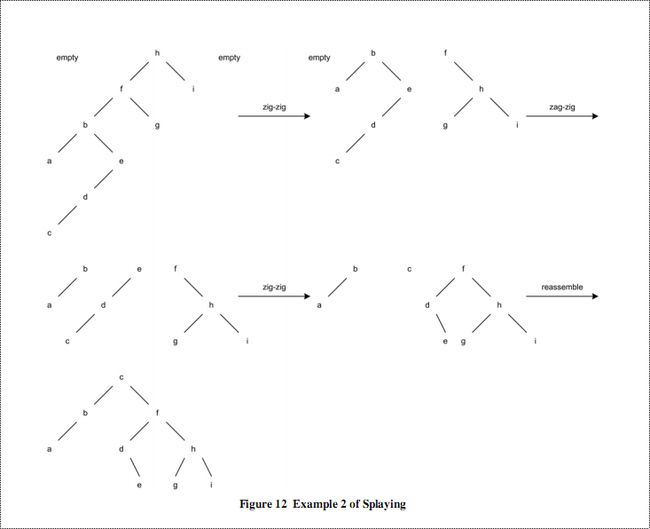
分割线以下转自http://www.cnblogs.com/kernel_hcy/archive/2010/03/17/1688360.html
ps:crash大神的论文中提到
![]()
在伸展树中对区间进行操作首先我们认为伸展树的中序遍历即为我们维护的数列,那么很重要的一个操作就是怎么在伸展树中表示任意一个区间。比如我们要提取区间[a,b],那么我们将a前面一个数对应的结点转到树根,将b 后面一个结点对应的结点转到树根的右边,那么根右边的左子树就对应了区间[a,b]。其中的道理也是很简单的,将a 前面一个数对应的结点转到树根后, a 及a 后面的数就在根的右子树上,然后又将b后面一个结点对应的结点转到树根的右边,那么[a,b]这个区间就是图三中*所示的子树。
splay模板
#include
using namespace std;
#define MAXN 100010
struct Node{
int key, sz, cnt;
Node *ch[2], *pnt;//左右儿子和父亲
Node(){}
Node(int x, int y, int z){
key = x, sz = y, cnt = z;
}
void rs(){
sz = ch[0]->sz + ch[1]->sz + cnt;
}
}nil(0, 0, 0), *NIL = &nil;
struct Splay{//伸展树结构体类型
Node *root;
int ncnt;//计算key值不同的结点数,注意已经去重了
Node nod[MAXN];
void init(){// 首先要初始化
root = NIL;
ncnt = 0;
}
void rotate(Node *x, bool d){//旋转操作,d为true表示右旋
Node *y = x->pnt;
y->ch[!d] = x->ch[d];
if (x->ch[d] != NIL)
x->ch[d]->pnt = y;
x->pnt = y->pnt;
if (y->pnt != NIL){
if (y == y->pnt->ch[d])
y->pnt->ch[d] = x;
else
y->pnt->ch[!d] = x;
}
x->ch[d] = y;
y->pnt = x;
y->rs();
x->rs();
}
void splay(Node *x, Node *target){//将x伸展到target的儿子位置处
Node *y;
while (x->pnt != target){
y = x->pnt;
if (x == y->ch[0]){
if (y->pnt != target && y == y->pnt->ch[0])
rotate(y, true);
rotate(x, true);
}
else{
if (y->pnt != target && y == y->pnt->ch[1])
rotate(y, false);
rotate(x, false);
}
}
if (target == NIL)
root = x;
}
/************************以上一般不用修改************************/
void insert(int key){//插入一个值
if (root == NIL){
ncnt = 0;
root = &nod[++ncnt];
root->ch[0] = root->ch[1] = root->pnt = NIL;
root->key = key;
root->sz = root->cnt = 1;
return;
}
Node *x = root, *y;
while (1){
x->sz++;
if (key == x->key){
x->cnt++;
x->rs();
y = x;
break;
}
else if (key < x->key){
if (x->ch[0] != NIL)
x = x->ch[0];
else{
x->ch[0] = &nod[++ncnt];
y = x->ch[0];
y->key = key;
y->sz = y->cnt = 1;
y->ch[0] = y->ch[1] = NIL;
y->pnt = x;
break;
}
}
else{
if (x->ch[1] != NIL)
x = x->ch[1];
else{
x->ch[1] = &nod[++ncnt];
y = x->ch[1];
y->key = key;
y->sz = y->cnt = 1;
y->ch[0] = y->ch[1] = NIL;
y->pnt = x;
break;
}
}
}
splay(y, NIL);
}
Node* search(int key){//查找一个值,返回指针
if (root == NIL)
return NIL;
Node *x = root, *y = NIL;
while (1){
if (key == x->key){
y = x;
break;
}
else if (key > x->key){
if (x->ch[1] != NIL)
x = x->ch[1];
else
break;
}
else{
if (x->ch[0] != NIL)
x = x->ch[0];
else
break;
}
}
splay(x, NIL);
return y;
}
Node* searchmin(Node *x){//查找最小值,返回指针
Node *y = x->pnt;
while (x->ch[0] != NIL){//遍历到最左的儿子就是最小值
x = x->ch[0];
}
splay(x, y);
return x;
}
void del(int key){//删除一个值
if (root == NIL)
return;
Node *x = search(key), *y;
if (x == NIL)
return;
if (x->cnt > 1){
x->cnt--;
x->rs();
return;
}
else if (x->ch[0] == NIL && x->ch[1] == NIL){
init();
return;
}
else if (x->ch[0] == NIL){
root = x->ch[1];
x->ch[1]->pnt = NIL;
return;
}
else if (x->ch[1] == NIL){
root = x->ch[0];
x->ch[0]->pnt = NIL;
return;
}
y = searchmin(x->ch[1]);
y->pnt = NIL;
y->ch[0] = x->ch[0];
x->ch[0]->pnt = y;
y->rs();
root = y;
}
int rank(int key){//求结点高度
Node *x = search(key);
if (x == NIL)
return 0;
return x->ch[0]->sz + 1/* or x->cnt*/;
}
Node* findk(int kth){//查找第k小的值
if (root == NIL || kth > root->sz)
return NIL;
Node *x = root;
while (1){
if (x->ch[0]->sz +1 <= kth && kth <= x->ch[0]->sz + x->cnt)
break;
else if (kth <= x->ch[0]->sz)
x = x->ch[0];
else{
kth -= x->ch[0]->sz + x->cnt;
x = x->ch[1];
}
}
splay(x, NIL);
return x;
}
}sp;
int main(){
sp.init();
sp.insert(10);
sp.insert(2);
sp.insert(2);
sp.insert(2);
sp.insert(3);
sp.insert(3);
sp.insert(10);
for (int i = 1; i <= 7; i++)
cout << sp.findk(i)->key << endl;
cout<key< 数组版 http://code.bulix.org/w8s75i-81022