TripleGAN
NIPS 2017 《Triple Generative Adversarial Nets》
github

在《Coupled Generative Adversarial Networks》中,作者使用了两个GANs实现了在无配对数据的的情况下,实现不同的domain之间的高层次的特征学习。除了couple GAN,类似的还有这篇文章所讲的TripleGANs,但它并不是直面理解的使用了三个GAN,而是在GAN中添加了一个分类器(classifier)。
背景
在这篇文章发表之前,在半监督学习方面,GANs已经取得一些不错的成果,但是它们存在两个问题:
- 生成器 G G G和判别器 D D D无法各自都达到最优
- 生成器 G G G无法掌握生成样本中的语义信息
对于第一个问题,有人使用了feature matching的技术,但是它在分类方面效果不错,但无法产生逼真的图像;也有人使用了minibatch discrimination的技术,但它可以产生逼真的图像,却无法同时在分类方面做的很好。
对于第二个问题,因为生成样本中的语义特征对于之后的应用很关键,所以从中提取出有意义的语义特征也是一件很重要的事情,为了解决这个问题,在其他的GAN的变种中也有专门的解决方案。
作者认为这两个问题的出现,主要是由于在传统的GAN中, G G G、 D D D双方博弈的过程使得 D D D无法同时兼容两个角色,既判别输入的样本是来自真实数据分布还是生成器,同时预测数据的类标签。这样的做法只能关注到数据的一部分信息,即数据的来源,而无法考虑到数据的类标签信息。
为了解决这个问题,在标准的GAN的基础上引入了分类器 C C C,这样它就有了三个部分 G 、 D 、 C G、D、C G、D、C,因为取名TripleGAN。G和C分别对图像和标签之间的条件分布进行特征描述,而D只需要专注于判别输入样本image-label的来源。
通过这样的做法,除了解决上面提出的两个问题,TripleGAN还有如下的优势:
- 可以实现很好的分类效果
- 通过在潜在的条件类空间中插值,实现输入样本在类和风格样式的分解,并在数据空间中平滑传输
整体理解
TripleGAN的结构如下所示:
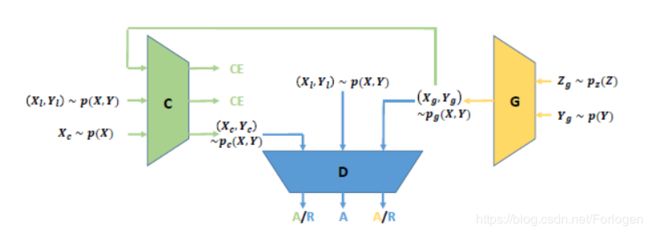
其中 R R R表示拒绝, A A A表示接受, C E CE CE表示监督学习的交叉熵损失。 p g p_{g} pg、 p c p_{c} pc和 p p p分别是由生成器、分类器和真实数据生成过程定义的分布, C E CE CE是保证它们之间一致性的无偏正则化。
上图中的 G G G和 C C C是两个条件网络, C C C为真实的图像数据生成伪标签, G G G给真实标签对应的假的图像数据, D D D 只用判别输入的data-label是否来自真实的带标签的数据集。通过 C C C和 G G G之间不断地对抗学习,最终可以同时得到不错的 C C C和 G G G,而且 D D D可以从 C C C得到关于无标签数据的标签信息,迫使 G G G生成正确的image-label数据。这样就解决了其他GANs无法解决的两个问题,并通过理论分析和实验分析,验证了TripleGAN最后可以学习到一个好的分类器和一个好的条件生成器。
理论分析
TripleGAN的目标不仅是可以为无标签的数据正确的预测对应的类标签,而且还可以生成真实的data-label数据。
P ( x , y ) = P ( x ) P ( y ∣ x ) P ( x , y ) = P ( y ) P ( x ∣ y ) P(x,y)=P(x)P(y|x)\\ P(x,y)=P(y)P(x|y) P(x,y)=P(x)P(y∣x)P(x,y)=P(y)P(x∣y)
首先我们先对TripleGAN中的各部分做一些假设:
- C C C:描述了条件分布 P c ( x , y ) ≈ P ( y ∣ x ) P_{c}(x,y) \approx P(y|x) Pc(x,y)≈P(y∣x)
- G G G:描述了条件分布 P G ( x , y ) ≈ P ( x ∣ y ) P_{G}(x,y) \approx P(x|y) PG(x,y)≈P(x∣y)
- D D D:判别 ( x , y ) (x,y) (x,y)是否来自真是数据分布 P ( x , y ) P(x,y) P(x,y)
理想的博弈的最优均衡点出现在,当 C C C和 G G G定义的条件分布都收敛于真实数据分布 p ( x , y ) p(x,y) p(x,y) 的情况下。
- p ( x ) 、 p ( y ) p(x)、p(y) p(x)、p(y):分别表示真实数据集中的边缘分布
- x x x: x = G ( y , z ) x = G(y,z) x=G(y,z),表示生成器生成的假样本
- p c ( x , y ) p_{c}(x,y) pc(x,y): p c ( x , y ) = p ( x ) p ( y ∣ x ) p_{c}(x,y)=p(x)p(y|x) pc(x,y)=p(x)p(y∣x),表示分类器生成的data-label数据
- p g ( x , y ) p_{g}(x,y) pg(x,y): p g ( x , y ) = p ( y ) p ( x ∣ y ) p_{g}(x,y)=p(y)p(x|y) pg(x,y)=p(y)p(x∣y),表示生成器生成的data-label数据
- p ( x , y ) p(x,y) p(x,y):表示从真实数据分布中采样的data-label数据
将 p c ( x , y ) p_{c}(x,y) pc(x,y)、 p g ( x , y ) p_{g}(x,y) pg(x,y)、 p ( x , y ) p(x,y) p(x,y)都输入到 D D D中,让其进行判别。那么三者之间的对间过程如下所示:
min C , G max D U ( C , G , D ) = E ( x , y ) ∼ p ( x , y ) [ log D ( x , y ) ] + α E ( x , y ) ∼ p c ( x , y ) [ log ( 1 − D ( x , y ) ) ] + ( 1 − α ) E ( x , y ) ∼ p g ( x , y ) [ log ( 1 − D ( G ( y , z ) , y ) ) ] \begin{aligned} \min _{C, G} \max _{D} U(C, G, D)=& E_{(x, y) \sim p(x, y)}[\log D(x, y)]+\alpha E_{(x, y) \sim p_{c}(x, y)}[\log (1-D(x, y))] \\ &+(1-\alpha) E_{(x, y) \sim p_{g}(x, y)}[\log (1-D(G(y, z), y))] \end{aligned} C,GminDmaxU(C,G,D)=E(x,y)∼p(x,y)[logD(x,y)]+αE(x,y)∼pc(x,y)[log(1−D(x,y))]+(1−α)E(x,y)∼pg(x,y)[log(1−D(G(y,z),y))]
其中 α \alpha α为平衡生成和分类重要性的超参数,本文设置 α = 1 2 \alpha=\frac{1}{2} α=21。当且仅当 p ( x , y ) = ( 1 − α ) p g ( x , y ) + α p c ( x , y ) p(x,y)=(1-\alpha)p_{g}(x,y)+\alpha p_{c}(x,y) p(x,y)=(1−α)pg(x,y)+αpc(x,y)时,才能到达均衡点。但是很难确保当 p ( x , y ) = p g ( x , y ) = p c ( x , y ) p(x,y)=p_{g}(x,y)=p_{c}(x,y) p(x,y)=pg(x,y)=pc(x,y) 时为唯一的全局最优点,为此在 C C C中引入了standard supervised loss,定义如下:
R L = E ( x , y ) ∼ p ( x , y ) [ − log p c ( y ∣ x ) ] \mathcal{R}_{\mathcal{L}}=E_{(x, y) \sim p(x, y)}\left[-\log p_{c}(y | x)\right] RL=E(x,y)∼p(x,y)[−logpc(y∣x)]
它相当于衡量 p c ( x , y ) p_{c}(x,y) pc(x,y)和 p ( x , y ) p(x,y) p(x,y) 之间的KL散度,因为只要 C C C和 G G G中有一个趋近于数据的真实分布,另一个也会同样趋近于真实数据分布,所以这里选择一个方向即可。因此objective function转换成如下的形式:
min C , G max D U ~ ( C , G , D ) = E ( x , y ) ∼ p ( x , y ) [ log D ( x , y ) ] + α E ( x , y ) ∼ p c ( x , y ) [ log ( 1 − D ( x , y ) ) ] + ( 1 − α ) E ( x , y ) ∼ p g ( x , y ) [ log ( 1 − D ( G ( y , z ) , y ) ) ] + R L \begin{aligned} \min _{C, G} \max _{D} \tilde{U}(C, G, D)=& E_{(x, y) \sim p(x, y)}[\log D(x, y)]+\alpha E_{(x, y) \sim p_{c}(x, y)}[\log (1-D(x, y))] \\ &+(1-\alpha) E_{(x, y) \sim p_{g}(x, y)}[\log (1-D(G(y, z), y))]+\mathcal{R}_{\mathcal{L}} \end{aligned} C,GminDmaxU~(C,G,D)=E(x,y)∼p(x,y)[logD(x,y)]+αE(x,y)∼pc(x,y)[log(1−D(x,y))]+(1−α)E(x,y)∼pg(x,y)[log(1−D(G(y,z),y))]+RL
文中证明了 U ~ \tilde{U} U~对于 C C C和 G G G有唯一的全局最优点。
整体的算法描述如下所示:

更多有关理论方面的证明,可见原论文的3.2和附录部分,很容易理解。
实验
作者在MNIST、SVHN、CIFAR0三个数据集上做了实验,分别和其他的相关算法进行比较,显示了TripleGAN分类的效果明显由于其他的算法,甚至好于ImprovedGAN。
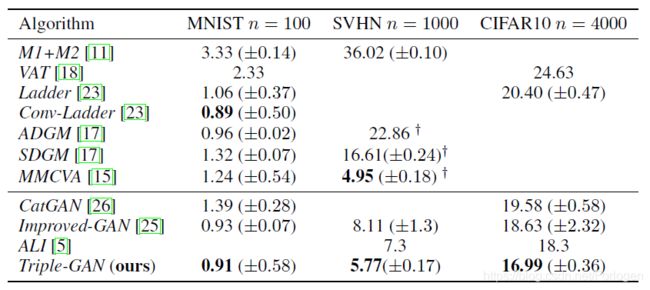
而且当带标签数据减少时,TripleGAN的分类效果也要优于ImprovedGAN。
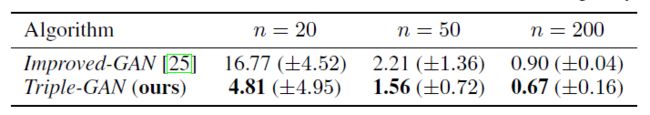
生成实验中,在MNIST上的生成效果优于使用feature matching的ImprovedGAN

在CIFAR10上生成的图像的效果也很好

总结
TripleGAN相比于其他的GANs,在数据方面而言,它不仅是可以生成效果较好的图像,同时还利用了图像的类标签信息。因此可以使用TripleGAN中的生成器,为指定的类标签生成样本;也可以使用其中的分类器,为图像打标签。综合来看,使用TripleGAN可以丰富训练的数据集,减少人工标注的开销。