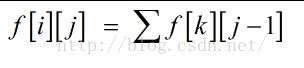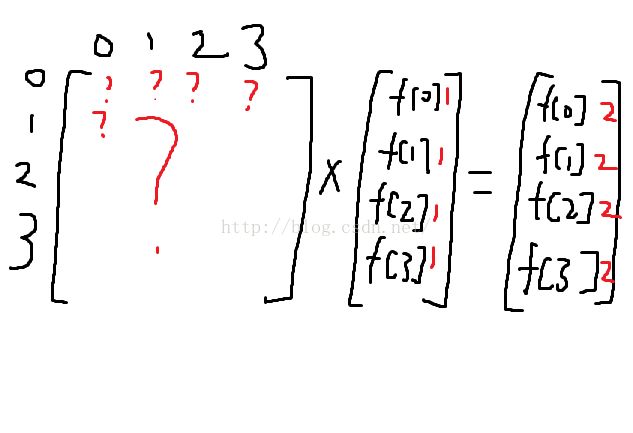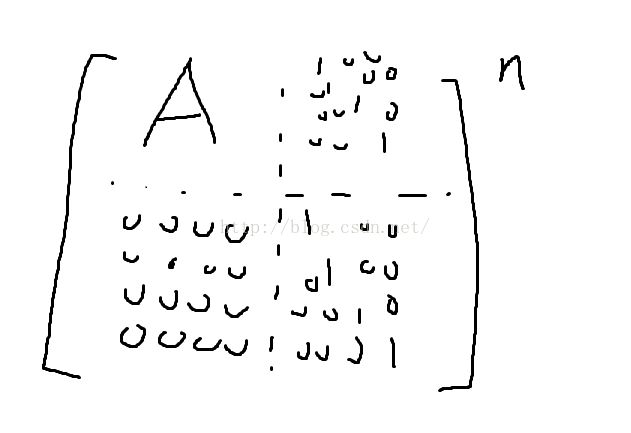题目大意:
给一些字母串,问长度为L【以内】的全部字母串中,有多少个字母串,【包含】给定的字母串。答案mod 2^64
首先,对于答案mod 2^64,只要全部使用unsigned long long进行运算,就会自动实现这个功能了。
然后假设,问题只求长度为L,而不是长度小于L的,这个问题怎么做呢?
参考前一个题解……
题目转换为求【不包含】给定字母串来做的话,会简单一些。求出不包含的数量,和总数,做差即可。
这里再简述一下,构造AC自动机,我们然后我们知道对于trie图中,有些节点不能到达,一旦到达,说明这个方案不合法。
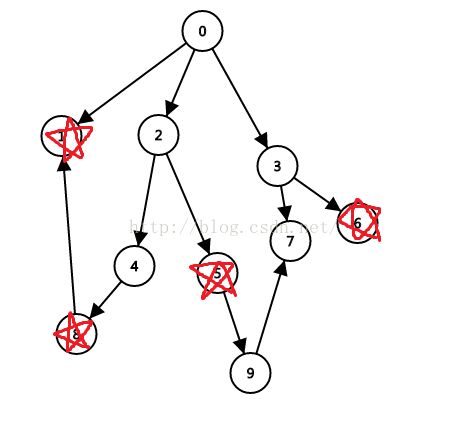
对于上图的AC自动机(省略了无数条边……)
红色的节点,为那个节点表示,到那个节点有单词出现。
(考虑AC自动机的last指针,不能只考虑val来考虑是否有单词,因为对于abcdefgpp,和efg。可能遍历到abcdefgp的时候,已经有efg了,所以abcdefg的g的位置,也是不可访问的)
现在问题就变为了,在trie图中跑路~ 从0出发,经过L步,不经过红色点的方案总数。
f[i][j]表示,停留在AC自动机的i节点,走了j步的方案总数。
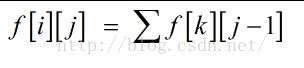
其中k节点可以到i节点,并且k,j节点都不是红色节点。
暴力转移必然TLE。 这样的式子可以矩阵优化。
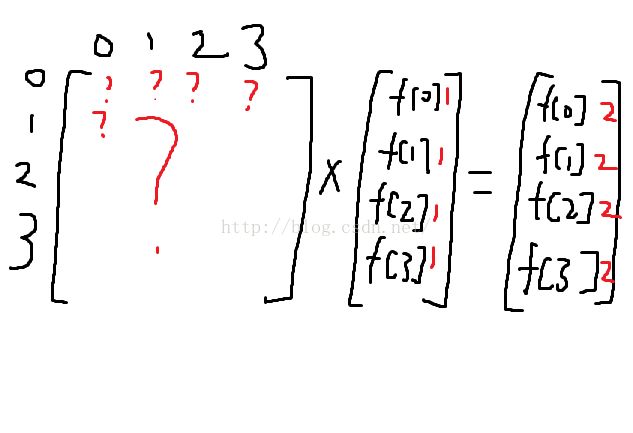
这样的矩阵。中间的矩阵保存f[0][i],经过一次乘法后,得到f[0][i+1]
左边的矩阵意淫一下就可以知道,a[i][j]表示f[j]是否可以转移到f[i],是的话就是1,否则就是0.
然后矩阵乘法满足结合律……就可以实现快速求出结果了。 当然这是HDU 2222的题解~~~~
这题需要的是矩阵的1次方,2次方,3次方。。。n次方的和。
对于a^0+a^1+a^2+a^3+++++a^n 的求解,也可以借助矩阵实现。

就是这个矩阵! 当然也可以推导出(3*3) * (3*1)的矩阵的形式。但是既然有2*2的矩阵,当然好啦。
这个矩阵的n次方后的第一行的元素之和,就是a^0+a^1+a^2++++a^n啦。 (1)
当然,现在我们的a是一个矩阵。 矩阵也可以实现的~
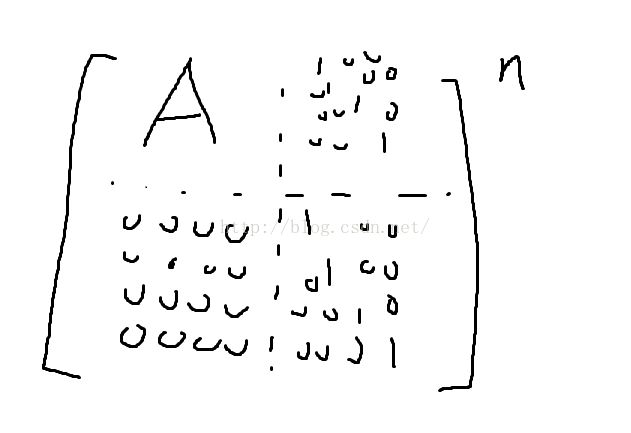
就是这样~ 左上角是矩阵,然后右边一列,是2个大大的单位矩阵。
然后这个矩阵的n次方后,把第一行的2个大矩阵相加,就是A^0+A^1+A^2+++A^n啦。
当然,矩阵的0次方,就是单位矩阵。
这题用这个方法,就可以快速求出方案总数。(包含不经过红色点的方案总数,任何排列的26^1+26^2……26^L的方案总数)
我们求出来的是26^0+26^1...+26^L, 以及矩阵A^0+A^1+A^2++++A^n的方案总数。
看起来是不是多了一个26^0,右边多了一个A^0呢?
左边对于26^0,直接答案减1即可。
右边多了一个A^0,可以去掉一个单位矩阵。当然,可以看出A^0 * b(b就是f[0],f[1]的那个矩阵),单位矩阵乘以那个矩阵,就是那个矩阵本身。而那个矩阵本身,也就走0步的状态的方案总数,也就是26^0的方案总数~ 所以可以不用考虑。 (这一段话比较混乱,大家可以自行理解)
矩阵乘法板子
const int mat_size = 40 * 2;//矩阵大小,需要乘以2,为了&运算的时候需要二倍的矩阵大小
struct Matrix
{
unsigned long long a[mat_size][mat_size];
int x, y;//长宽
Matrix() //返回0矩阵
{
memset(a,0,sizeof(a));
}
Matrix(int x,int y)//返回0矩阵,并且x,y赋值
{
this->x = x;
this->y = y;
memset(a, 0,sizeof(a));
}
Matrix(int n) //返回n*n的【单位矩阵】
{
this->x=n;
this->y=n;
memset(a,0,sizeof(a));
for (int i = 0; i >= 1 ;
A = A * A ;
}
return ret ;
}
Matrix operator & (int b)//A^0 + A^1+A^2+A^3+++A^n,其中A是矩阵。最后返回的就是一个矩阵
{
Matrix ret = *this;
for (int i = ret.x; i < ret.x * 2; ++ i)
{
ret.a[i-ret.x][i]= 1;
ret.a[i][i] = 1;
}
ret.x <<= 1;
ret.y <<= 1;
//pg(ret);
ret = ret^b;
ret.x >>= 1;
ret.y >>= 1;
for (int i = 0; i < ret.x; ++ i)
for (int j = 0; j < ret.y; ++ j)
ret.a[i][j] += ret.a[i][j + ret.x];
return ret;
}
void pg(Matrix A)
{
for (int i = 0; i
ac code : 46ms
#include
#include
#include
#include
#include
#include
#include