数据标准化与PCA白化原理探索
PCA是实验中很常用的工具,一般用来做降维,它的实现有很多很多种,其中牵涉相当多的细节,笔者在实现PCA时常常有困惑,为什么查到的各种代码总有一些不同的trick,有时候对样本提前归一化?有时候又要减均值?这些操作对于PCA降维效果到底有什么影响?这篇文章从PCA白化入手,探究这些trick背后的原因。
1 Whitening (白化)
白化1有两种,一种是PCA Whitening,一种是ZCA Whitening,它主要目标是降低数据的冗余性,我们希望通过白化过程使得学习算法的输入具有如下性质:
- 特征之间相关性较低;
- 所有特征具有相同的方差。
2 Standardize(标准化)
标准化有多种实现方式,其目标是使数据均值为0,方差为1,使得不同维度的特征具有同等重要性。因为不同维度的特征代表的信息不同,数值变化范围会有较大差异,如果统一衡量将可能影响判断。
在PCA中融入standardize就是PCA whitening。
2.1 举例说明Standardize重要性
那么standardize有什么好处?看一个来自StackExchange的例子2:
用一个特征来描述一棵树,它是二维的,第一维是高度height,第二维是切面周长girth,我们要根据这个二维特征,来推断一棵树的体积volume是low还是high(设大于20为high)。
我们分以下三种情况来分析:
2.1.1 Different measure
先看一种比较极端的情况,让height的单位是mile,girth的单位是feet,1mile=5280feet=1.6km,也就是说,height的值将是很小的小数,我们假设height取值范围是[0,0.05],而girth的值取值范围可以假设为[20,50],一个树的height那一维的特征从0.04变为0.05,相对于girth已经可以小的忽略不计了,但是它在自己的取值范围上变化了15,从直观上看这是必须考虑的,所以我们要增大这种数值小,数值范围小的特征的影响。
分析主成分
Comp.1 Comp.2
Standard deviation 3.0871086 1.014551e-03
Loadings: tree.height -1
tree.girth 1
画图分析,其中灰色的low/high指的是volume,红线height和girth的走势是根据loading画出的,loading指的是原始特征在component上保留的方差,可以看出,height的方差主要反映在component2上,girth的方差反映在component1上,而由于height的重要性被girth完全压制,故在图中可以看到,volume的low/high完全靠girth来决定,girth越大,volume越大,height的信息完全没有起到作用。而我们知道事实上,一棵树的体积肯定跟高度是有关系的。 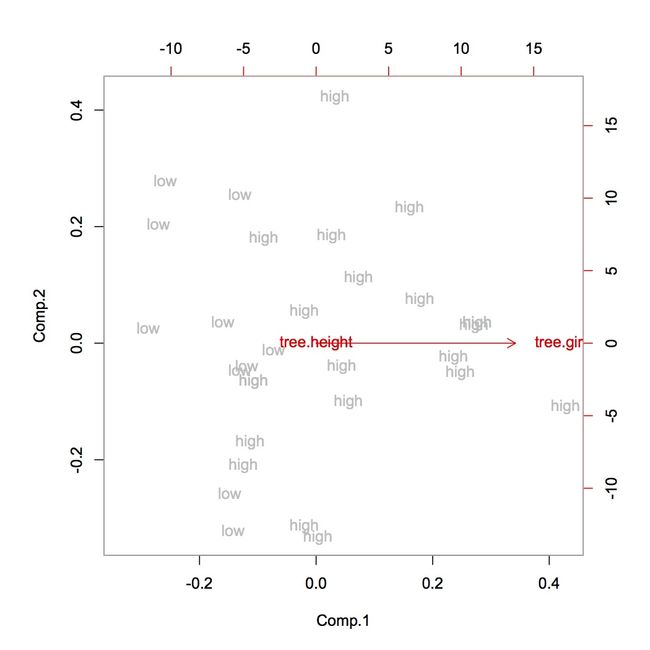
2.1.2 Same measure without standarized
进一步地,让height和girth单位一致,即都是feet。
分析其主成分:
Comp.1 Comp.2
Standard deviation 6.5088696 2.5407042
Loadings: tree.height -0.956 0.293
tree.girth -0.293 -0.956从图中可以看出,height的红线较长,代表volume对height较敏感。因为component1的方差大,即变化范围大,而原始数据height那一维的数据的方差较多地反映在component1上,因此height起到较大影响。这是因为一棵树的height变化范围比girth变化范围大。但是实际上,根据树的体积计算公式,我们知道,树的girth应该起较大作用。
2.1.3 Standarized
至此,来看看standardize的结果。
分析其主成分:
Comp.1 Comp.2
Standard deviation 0.2275561 0.06779544
Loadings: tree.height 0.203 -0.979
tree.girth 0.979 0.203由图可以看出,girth对volume的判断起到较大作用,符合客观事实。 
3 PCA whitening
假设我们已经通过公式SU=LU 计算得到了PCA的主成份:L的对角线元素是特征值由大到小排列,U是特征值对应的特征向量,S是原始数据x的协方差矩阵。
下式就是PCA whitening操作,计算yn是第n个样本白化的结果。
下式验证白化后的数据方差为1.
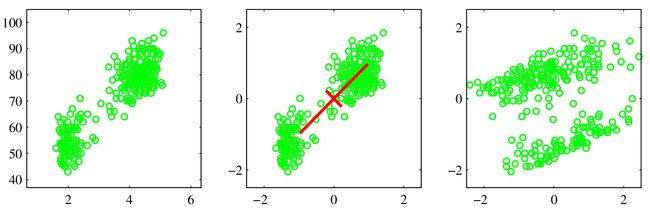
下图 3中:左边是原始数据,中间是standardize的结果,右边是PCA whitening的结果,我们可以看到数据散开,主成份没有明显的长短轴,差异性被进一步挖掘。
- 白化介绍 ↩
- Standardize的解释 ↩
- 《Pattern Recognition and Machine Learning》 ↩