白化Whitening

白化操作的目的是让我们的减少冗余信息，准确来说通过白化操作我们有两个目的：

• 每个特征之间关联性更少
• 每个特征有相同的方差
  对于第一个目的来说，我们可以通过熟悉的PCA来实现。

PCA

Principal Components Analysis (PCA) 是一个用来减少特征纬度的算法，它通过减少特征的纬度来减少冗余信息。

比如说，下图所示的一个特征纬度为2的点分类问题，我们可以看到数据的主要分布在y=x这条线周围。

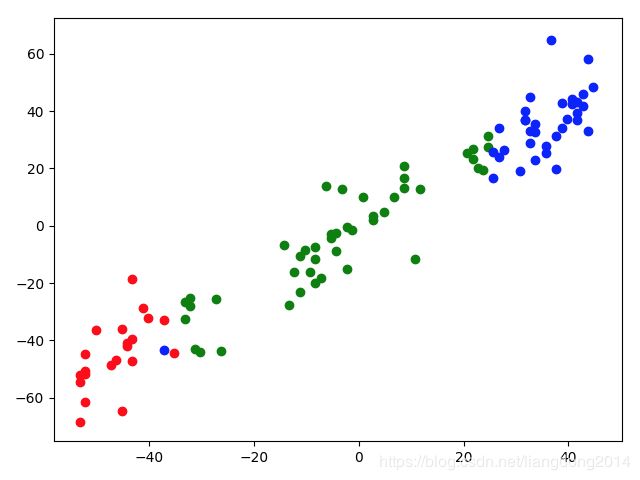
• 我们再回顾一下PCA的计算流程
  • 首先计算数据的协方差矩阵$\Sigma$
  • 接下来对数据进行特征值分解
  • 使用原始数据分布乘以特征向量，得到新的特征空间的表示
• 统一期间，我们用$r_i$表示第$i$个example的向量，它是一个列向量(纬度是$K$)。$X$表示整个数据集,shape是$K\ast N$,$N$是样本的个数
• 如果数据集的均值不在0点，则$X=X-mea{n}_X$将数据的中心点移动到0点。
• 然后计算$\Sigma$, $\Sigma =\frac{1}{N}{\sum }_{i=0}^{i=N}{r}_i{r}_i^T$，所以$\Sigma$的shape是$K\ast K$
• 然后计算进行特征值分解，将特征向量，按照特征值的大小进行排序。得到$u_1,u_2,...,u_k$ 以及 ${\lambda }_1,{\lambda }_2,...,{\lambda }_k$，其中${\lambda }_1>{\lambda }_2>...>{\lambda }_k$
• 至此，我们可以得到一个$r_i$在新空间的表示$r_i^{{}^{\prime }}=(u_1^T\ast r_i,u_2^T\ast r_i,...,u_k^T\ast r_i)$。
• 那么怎么从K个纬度中选择出有效的信息呢？我们需要在有效性和效率之间有所平衡。假设说我们规定选择的信息占全部信息的90%即可。那怎么度量这个占比呢？我们假设信息占比标记为$ϵ=\frac{{\sum }_{i=1}^{K_s}{\lambda }_i}{{\sum }_{i=1}^K{\lambda }_i}$。其中$K_s$代表的是我们选择的特征的个数。
• 至此，我们已经可以得到在新的向量空间的特征，并且也可以减少冗余信息。注意⚠️，我们得到的新的特征，每个特征之间是彼此独立的。他们是原有的特征乘以相互正交的向量得到的。
• 在PCA的最后，我们可以可视化一下最后的结果。结果如下所示。可以看到经过处理后，相当于将原来的向量旋转到了和X轴平行的位置。此时X轴的坐标就是在原来坐标空间方差最大方向的坐标。
  

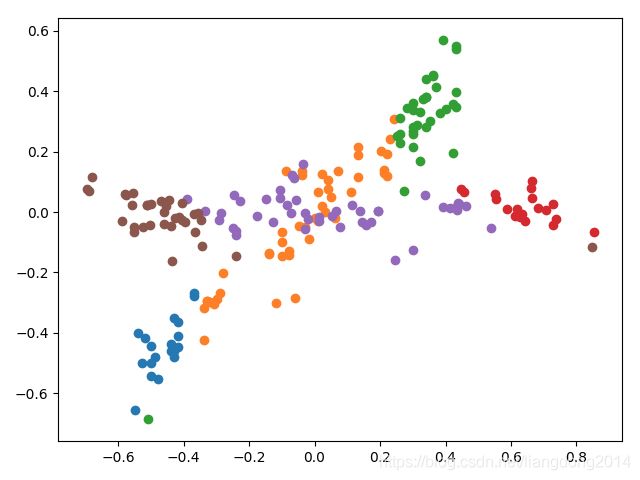
PCA Whitening

• 至此，我们已经可以完成第一个目标了，即就是操作后每个特征之间关联性更少。那么怎么完成第二个目标呢？即就是每个特征有相同的方差。
• PCA whitening的操作方式是$r_{i_{whitening}}=\frac{r_{i_{PCA}}}{{\lambda }_i}$就是对PCA计算得到的特征向量的每一纬度再除以一个对应的特征值(表示的就是方差)。除以方差之后，就可以让每个特征值的范围差距不会特别大。
• 接下来给大家展示一下白化后的效果
  

ZCA whitening

• ZCA whitening是在PCA whitening的基础上再将坐标transform到原来的坐标系，具体的公示如下:
  $r_{i_{ZCA}}=r_{i_{PCA}}\ast U^T$

代码

# -*- coding=utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets


def draw_points(data, label):
    color = ['r', 'g', 'b']
    for idx in np.unique(label):
        # plt.scatter(x=data[np.argwhere(label == idx), 0], y=data[np.argwhere(label == idx), 1], c=color[idx])
        plt.scatter(x=data[np.argwhere(label == idx), 0], y=data[np.argwhere(label == idx), 1])
    # plt.yticks([-0.5, 0.5])


def load_data():
    # digits = datasets.load_digits()
    # xs = digits.data
    # ys = digits.target
    # print(np.shape(xs), np.shape(ys))
    xs_1 = np.random.randint(0, 30, [30, 1])
    xs_2 = np.random.randint(40, 70, [30, 1])
    xs_3 = np.random.randint(75, 100, [40, 1])
    xs = np.concatenate([xs_1, xs_2, xs_3], axis=0)
    ys = []
    for x in xs:
        flag = np.random.random()
        if flag > 0.5:
            ys.append(x + np.random.random() * np.random.randint(30))
        else:
            ys.append(x - np.random.random() * np.random.randint(30))
    # ys = xs + np.random.random([100, 1]) * 5
    ys = np.asarray(ys, np.float32)
    index_1 = np.argwhere(xs <= 20)
    index_2 = np.argwhere(np.logical_and(xs > 20, xs < 80))
    index_3 = np.argwhere(xs >= 80)
    label = np.asarray(range(100), np.int32)
    label[index_1] = 0
    label[index_2] = 1
    label[index_3] = 2
    data = np.asarray(np.concatenate([xs, ys], axis=-1), np.float32)
    data[:, 0] /= 10
    data[:, 1] /= 100
    data -= np.mean(data, axis=0)
    print('the shape of data is ', np.shape(data))
    return data, label


def PCA(data):
    # 首先将中心点的位置调整至原点。即就是均值为0
    avg = np.mean(data, axis=0)
    data = data - avg

    # 计算协方差矩阵
    data = np.mat(data)
    sigma = data.T * data / len(data)
    print('The shape of Sigma is ', np.shape(sigma))
    print('The Sigma is ', sigma)
    eigenvectors, eigenvalues, _ = np.linalg.svd(sigma)
    print('the eigenvalues is ', eigenvalues)
    print('the eigenvectors is ', eigenvectors)
    data_rot = data * eigenvectors
    # draw_points(np.asarray(data_rot, np.float32), label)
    return data_rot, eigenvalues, eigenvectors


def PCA_whitening(data, select_k):
    data_rot, eigenvalues, eigenvectors = PCA(data)
    data_whitening = np.copy(data_rot[:, select_k])
    data_whitening[:, 0] /= np.sqrt(eigenvalues[0])
    data_whitening[:, 1] /= np.sqrt(eigenvalues[1])
    # draw_points(data_whitening, label)
    return data_whitening, eigenvalues[:select_k], eigenvectors[:, :select_k]


def ZCA_whitening(data, select_k):
    data_whitening_pca, _, eigenvectors = PCA_whitening(data, select_k)
    print(np.shape(data_whitening_pca), np.shape(eigenvectors))
    data_whitening = data_whitening_pca * eigenvectors.T
    print(np.shape(data_whitening))
    # draw_points(np.asarray(data_whitening, np.float32), label)
    return data_whitening


if __name__ == '__main__':
    data, label = load_data()
    # draw_points(data, label)
    # data_rot, eigenvalues = PCA(data, label)
    # draw_points(np.asarray(data_rot, np.float32), label)
    # PCA_whitening(data, label)
    data_whitening_zca = ZCA_whitening(data, select_k=1)
    draw_points(np.asarray(data_whitening_zca, np.float32), label)
    plt.show()

参考文献

• whitening