Flip Game-1753
Flip Game
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 35785 | Accepted: 15628 |
Description
Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces, thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules:
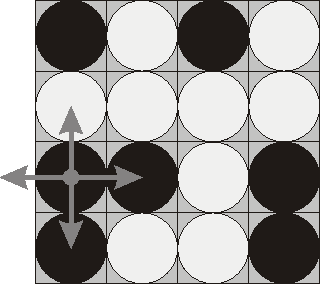Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
- Choose any one of the 16 pieces.
- Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).
Consider the following position as an example: bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.
Input
The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.
Output
Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible" (without quotes).
Sample Input
bwwb
bbwb
bwwb
bwww
Sample Output
4
Source
分析过程：
本题目的题意为：给你一个4*4的面板，面板上由黑色和白色两种颜色组成，当你翻转其中一个点时，这个点本身连同其周围的紧邻的各个点也随着一起翻转，问你当面板翻转成一种颜色（黑色或者白色）时，最少翻转多少次？
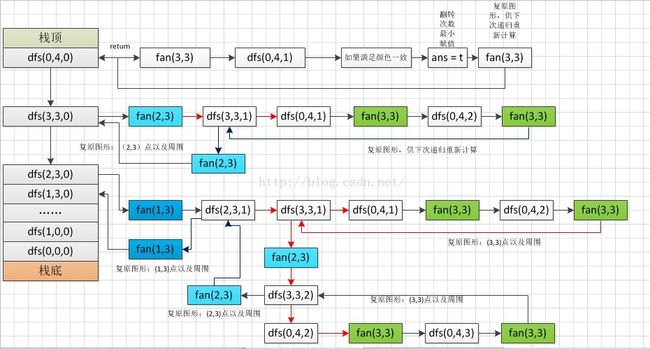
算法可以采用：DFS搜索和回溯，从第一个点开始搜索，（按列搜索或者按行搜索都可以，本方法采用按列搜索），当从(0,0)搜索到(3,3)最右下角元素时，再搜索就超过了面板的范围，此时用(0,4)作为回溯的起点，开始翻转并判断是否所有面板颜色一致？若一致就保存此次所用的翻转次数，如果没有达到一样的颜色，那就回溯到开始的下一个点，比如(2,3)，另外需要把你刚才翻转的(3,3)再进行翻转复原操作；当遍历整个点之后，就保存了最少翻转的次数，输出就可以了。
主要的算法核心为：
int
dfs
(
int
x
,
int
y
,
int
t
)
{
/*如果颜色都一致*/
if
(
panduan
())
{
/*把最小的次数t赋值给ans*/
if
(
ans
>
t
)
{
ans
=
t
;
}
return
0
;
}
/*如果超出范围则返回，递归退出条件*/
if
(
x
>=
4
||
y
>=
4
)
{
return
0
;
}
int
nx
,
ny
;
nx
=
(
x
+
1
)
%
4
;
ny
=
y
+
(
x
+
1
)
/
4
;
/*按列递归入栈，当为最右下角的元素dfs(3,3,0)后，再执行就为dfs(0,4,0)，然后return*/
dfs
(
nx
,
ny
,
t
);
fan
(
x
,
y
);
/*当fan(3,3)后假如全部为w，t为翻转次数加1，进入到dsf(0,4,1)后判断return 1*/
dfs
(
nx
,
ny
,
t
+
1
);
/*再把(3,3)复原回去，为了再次重新用新的栈顶元素重新操作，看有没有比记录的次数小*/
fan
(
x
,
y
);
return
0
;
}
其中对dfs算法采用了递归，递归的时候采用入栈出栈操作，先进入的dfs(0,0,0)作为栈底，后进入的dfs(0,4,0)作为栈顶，并设置出口条件：超过边界回溯+全部一样颜色时回溯；
下面的这张图，是根据算法来画的一张图，很清楚的表达了算法执行的流程：
整个代码如下：（注意，提交的时候需要选择C++，本人选C的时候老是编译错误）
![]()
/***********************************************************************
Copyright (c) 2015,wangzp
All rights no reserved.
Name: 《Flip Game》In PEKING UNIVERSITY ACM
ID: PROBLEM 1753
问题简述: 给出一个正方形4*4矩阵，每个点不是白色就是黑色
当你翻动一个点时，点的周围的点也要跟着翻动；
白色变黑色，黑色变白色，问最少需要用多少步使得板子颜色一致
算法描述：枚举+DFS+回溯。
Date: Oct 14, 2015
***********************************************************************/
#include
const int inf = 9999999;
char s[10];
int map[10][10],i,j;
int ans = inf;
/*判断是否全白色或者黑色*/
int panduan(void)
{
int x = map[0][0];
for (i = 0;i < 4;i++)
{
for (j = 0;j < 4;j++)
{
if (map[i][j] != x)
{
return 0;
}
}
}
return 1;
}
/*翻转算法，对于一个点有四种情况*/
void fan(int x,int y)
{
map[x][y] = !map[x][y];
if(x - 1 >= 0)
{
map[x-1][y] = !map[x-1][y];
}
if(x + 1 < 4)
{
map[x+1][y] = !map[x+1][y];
}
if(y - 1 >= 0)
{
map[x][y-1] = !map[x][y-1];
}
if(y + 1 < 4)
{
map[x][y+1] = !map[x][y+1];
}
}
/*深度搜索算法的实现*/
int dfs(int x,int y,int t)
{
/*如果颜色都一致*/
if (panduan())
{
/*把最小的次数t赋值给ans*/
if (ans > t)
{
ans = t;
}
return 0;
}
/*如果超出范围则返回，递归退出条件*/
if (x >= 4 || y >= 4)
{
return 0;
}
int nx,ny;
nx = (x + 1) % 4;
ny = y + (x + 1) / 4;
/*按列递归入栈，当为最右下角的元素dfs(3,3,0)后，再执行就为dfs(0,4,0)，然后return*/
dfs(nx,ny,t);
fan(x,y);
/*当fan(3,3)后假如全部为w，t为翻转次数加1，进入到dsf(0,4,1)后判断return 1*/
dfs(nx,ny,t+1);
/*再把(3,3)复原回去，为了再次重新用新的栈顶元素重新操作，看有没有比记录的次数小*/
fan(x,y);
return 0;
}
int main(void)
{
for (i = 0;i < 4;i++)
{
scanf ("%s",s);
/*初始化面板，0表示黑色，1表示白色*/
for (j = 0;j < 4;j++)
{
if (s[j] == 'b')
{
map[i][j] = 0;
}
else
{
map[i][j] = 1;
}
}
}
dfs(0,0,0);
if (ans == inf )
{
printf ("Impossible\n");
}
else
{
printf ("%d\n",ans);
}
return 0;
}