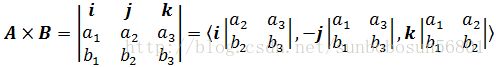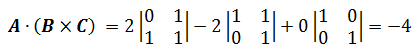线性代数笔记4——向量3（叉积）

什么是叉积

　　向量的叉积也叫外积、向量积、叉乘或矢量积。两个向量的叉积是这样表示的：

 

　　在二维空间内，向量A = 1, a₂>，B = 1, b₂>

 

　　其几何意义就是以两个向量为边的平行四边形的面积，这在上篇文章中给出了详细说明。

　　此外，叉积也适用于两个在三维空间内的向量。在三维空间内，向量A = 1, a₂, a₃>，B = 1, b₂, b₃>，C = 1, c₂, c₃>

 

　　i, j, k是三个维度中每个维度的单位向量，有点像三阶行列式，但并不是常理上的行列式，因为行列式不会出现向量，这里仅仅是为了便于表达和记忆。

　　从上面的描述中可以看出，叉积得到的是一个向量，而不是一个数字，也因此，A×B和B×A并不等同，实际上，

叉积的几何意义

　　向量的两个要素是模长和方向，让我们从这两个角度考虑叉积的几何意义。

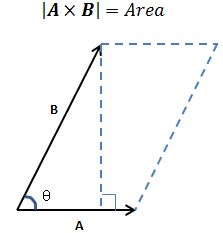
　　在模长上，叉积的几何意义是以两个向量为边的平行四边形的面积：

　　两个相同向量的叉积是0，

 

　　如果用几何意义解释，二者构成一条线段，线段的面积是0。

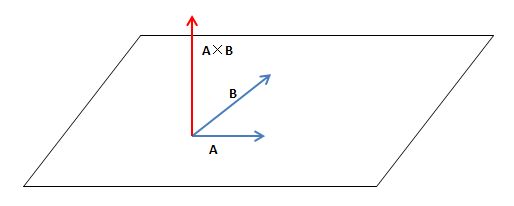
　　在方向上，叉积垂直于平行四边形所在的平面：

　　由于叉积存在负值，所以垂直的方向可能向上或向下，具体方向根据右手法则判断。

　　右手法则很有意思，首先要保持拇指朝上，然后其他四指指向叉积的第一个向量，向内弯曲四指指向另一个向量。如果两个向量的方向能符合这个手势，此时拇指的方向就是叉积的方向；如果必须向外弯曲四指，拇指的反方向是叉积的方向。总之，最终能够以一个舒服的方向竖起拇指就对了。

叉积的作用

计算平行六面体的体积

　　所谓平行六面体，就是六面体的每个面都是平行四边形，如下图所示：

　　向量H是垂直于底面的向量，|H|是六面体的高，可看作向量A在H方向上的分量，分量可以用点积表示，这在上一篇中叙述过。如果令u是H方向的单位向量：

 

判断点是否在同一平面

　　空间内的三点可以确定一个平面，P₁，P₂，P₃是空间中的三个点，另有一点P，如何判断P是否在平面内？

 

P是否在P₁，P₂，P₃组成的平面内？

　　可以借助向量通过上一节中平行六面体体积的知识判断，如下图所示：

 

　　这样形成了三个向量，|P₁P₃×P₁P₂| 是这两个向量围成的平行四边形的面积，P₁P·|P₁P₃×P₁P₂| 表示平行六面体的体积，如果体积是0，那么P就在平面内。

计算法向量

　　也可以用另一种方法求解上面的问题，这需要法向量的帮助。一个与平面垂直的向量称为该平面的法向量，一个平面有无数条法向量，法向量与一个常数的乘积还是法向量。

　　N是平面的法向量，如果N⊥P₁P，则P在平面内。根据点积的知识，N·P₁P = 0，则N⊥P₁P。如何计算N呢？实际上，N就是P₁P₃与P₁P₂的叉积。

　　如果P在平面内，则体积 = P₁P·（P₁P₃×P₁P₂）= 0；由于N⊥P₁P，N·P₁P = 0，结合二者：

P₁P·（P₁P₃×P₁P₂）= P₁P· N = 0

 => N = P₁P₃×P₁P₂

示例

示例1

　　平行六面体是三条边是三个向量<2, 2, 0>，<1, 0, 1>，<0, 1, 1>，求该六面体的体积。

　　很明显是相交于<0, 0, 0>的三个向量，设三个向量分别是A，B，C

 

　　体积是4

示例2

　　计算三个点围成的三角形的面积，P₁(-1, 0 , 1)，P₂(0, 2, 2)，P₃(0, -1, 2)

　　使用叉积很容易计算，需要注意的是，点积和叉乘仅对向量有意义，对点来说则毫无用处，所以首先需要将点转换为向量。