Nenu 复健训练#4 Codeforces Round 440 Div.2
A. Search for Pretty Integers
You are given two lists of non-zero digits.
Let's call an integer pretty if its (base 10) representation has at least one digit from the first list and at least one digit from the second list. What is the smallest positive pretty integer?
INPUT
The first line contains two integers n and m (1 ≤ n, m ≤ 9) — the lengths of the first and the second lists, respectively.
The second line contains n distinct digits
— the elements of the first list.
The third line contains m distinct digits 
— the elements of the second list.
OUTPUT
Print the smallest pretty integer.
Examples
Input
2 3
4 2
5 7 6
Output
25
Input
8 8
1 2 3 4 5 6 7 8
8 7 6 5 4 3 2 1
Output
1Note
In the first example 25, 46, 24567 are pretty, as well as many other integers. The smallest among them is 25. 42 and 24 are not pretty because they don't have digits from the second list.
In the second example all integers that have at least one digit different from 9 are pretty. It's obvious that the smallest among them is 1, because it's the smallest positive integer.
题意：给出两个数列，找出一个最小的数让其至少含有两个数列中一个数字，只需寻找两个数列是否有相同数字，否则排序后构造两位数
Code:
#include
#include
#include
#include
#include
#include
#include
#define res register int
#define dd double
#define ll long long
using namespace std;
const int maxn=1e3+12;
int n,m;int a[15],b[15];
int cmp(int a,int b){
return a B - Maximum of Maximums of Minimums
You are given an array 
consisting of n integers, and an integer k. You have to split the array into exactly k non-empty subsegments. You'll then compute the minimum integer on each subsegment, and take the maximum integer over the k obtained minimums. What is the maximum possible integer you can get?
Definitions of subsegment and array splitting are given in notes.
INPUT
The first line contains two integers n and k (1 ≤ k ≤ n ≤ 
) — the size of the array a and the number of subsegments you have to split the array to.
The second line contains n integers 
.
OUTPUT
Print single integer — the maximum possible integer you can get if you split the array into k non-empty subsegments and take maximum of minimums on the subsegments.
Examples
Input
5 2
1 2 3 4 5
Output
5
Input
5 1
-4 -5 -3 -2 -1
Output
-5Note
A subsegment ](http://img.e-com-net.com/image/info8/b6a9ff9937f54c1c8594708a29c239b7.gif){kind=small}
of array a is the sequence 
Splitting of array a of n elements into k subsegments ![[l_1,r_1],[l_2,r_2],...,[l_k,r_k](l_1=1,r_k=n,l_i=r_{i-1}+1\ for \ all\ i>1)](http://img.e-com-net.com/image/info8/be539e5ea2e541c0a28f3138f4482d50.gif){kind=small}
is k sequences
In the first example you should split the array into subsegments [1, 4] and [5, 5] that results in sequences (1, 2, 3, 4) and (5). The minimums are min(1, 2, 3, 4) = 1 and min(5) = 5. The resulting maximum is max(1, 5) = 5. It is obvious that you can't reach greater result.
In the second example the only option you have is to split the array into one subsegment [1, 5], that results in one sequence ( - 4, - 5, - 3, - 2, - 1). The only minimum is min( - 4, - 5, - 3, - 2, - 1) = - 5. The resulting maximum is - 5.
题意：题面看着很长其实很简单，将序列分成K个子段，计算子段的最小和，取最大整数，只需对K进行分类讨论即可
Code:
#include
#include
#include
#include
#include
#include
#include
#define res register int
#define dd double
#define ll long long
using namespace std;
const int maxn=1e5+12;
int s[maxn];
int cmp(int a,int b){
return a2){
sort(s+1,s+n+1,cmp);
printf("%d\n",s[n]);
}
memset(s,0,sizeof(s));
}
return 0;
} C. Maximum splitting
You are given several queries. In the 
query you are given a single positive integer 
. You are to represent as a sum of maximum possible number of composite summands and print this maximum number, or print -1, if there are no such splittings.
An integer greater than 1 is composite, if it is not prime, i.e. if it has positive divisors not equal to 1 and the integer itself.
INPUT
The first line contains single integer q (1 ≤ q ≤ ) — the number of queries.
q lines follow. The 
line contains single integer (1 ≤ n i ≤ 
) — the query.
OUTPUT
For each query print the maximum possible number of summands in a valid splitting to composite summands, or -1, if there are no such splittings.
Examples
Input
1
12
Output
3
Input
2
6
8
Output
1
2
Input
3
1
2
3
Output
-1
-1
-1题意：给出查询数字，判断此数字可拆分为最多合数的数量，如果没有则输出-1；
思路：数学问题，发现合数数量与最小合数4的关系并根据余数分类讨论，具体看代码
Code:
#include
#include
#include
#include
#include
#include
#include
#define res register int
#define dd double
#define ll long long
using namespace std;
const int maxn=1e3+12;
int n,q;
int main(){
scanf("%d",&q);
while(q--){
scanf("%d",&n);
if(n%4==0){
printf("%d\n",n/4);continue;
}
else{
int k=n/4;
if(n%4==1){
if(k>=2) printf("%d\n",k-1);
else printf("-1\n");
continue;
}
else if(n%4==2){
if(k>=1) printf("%d\n",k);
else printf("-1\n");
continue;
}
else if(n%4==3){
if(k>=3) printf("%d\n",k-1);
else printf("-1\n");
continue;
}
}
}
return 0;
} D - Something with XOR Queries
This is an interactive problem.
Jury has hidden a permutation p of integers from 0 to n - 1. You know only the length n. Remind that in permutation all integers are distinct.
Let b be the inverse permutation for p, i.e. 
for all i. The only thing you can do is to ask xor of elements p i and b j, printing two indices i and j (not necessarily distinct). As a result of the query with indices i and j you'll get the value 
, where 
denotes the xor operation. You can find the description of xor operation in notes.
Note that some permutations can remain indistinguishable from the hidden one, even if you make all possible n 2 queries. You have to compute the number of permutations indistinguishable from the hidden one, and print one of such permutations, making no more than 2n queries.
The hidden permutation does not depend on your queries.
INPUT
The first line contains single integer n (1 ≤ n ≤ 5000) — the length of the hidden permutation. You should read this integer first.
OUTPUT
When your program is ready to print the answer, print three lines.
In the first line print "!".
In the second line print single integer answers_cnt — the number of permutations indistinguishable from the hidden one, including the hidden one.
In the third line print n integers 
(0 ≤ p i < n, all 
should be distinct) — one of the permutations indistinguishable from the hidden one.
Your program should terminate after printing the answer.
Interaction
To ask about xor of two elements, print a string "? i j", where i and j — are integers from 0 to n - 1 — the index of the permutation element and the index of the inverse permutation element you want to know the xor-sum for. After that print a line break and make flush operation.
After printing the query your program should read single integer — the value of .
For a permutation of length n your program should make no more than 2n queries about xor-sum. Note that printing answer doesn't count as a query. Note that you can't ask more than 2n questions. If you ask more than 2n questions or at least one incorrect question, your solution will get "Wrong answer".
If at some moment your program reads -1 as an answer, it should immediately exit (for example, by calling exit(0)). You will get "Wrong answer" in this case, it means that you asked more than 2n questions, or asked an invalid question. If you ignore this, you can get other verdicts since your program will continue to read from a closed stream.
Your solution will get "Idleness Limit Exceeded", if you don't print anything or forget to flush the output, including for the final answer .
To flush you can use (just after printing line break):
- fflush(stdout) in C++;
- System.out.flush() in Java;
- stdout.flush() in Python;
- flush(output) in Pascal;
- For other languages see the documentation.
Hacking
For hacking use the following format:
Contestant programs will not be able to see this input.
Examples
Input
3
0
0
3
2
3
2
Output
? 0 0
? 1 1
? 1 2
? 0 2
? 2 1
? 2 0
!
1
0 1 2
Input
4
2
3
2
0
2
3
2
0
Output
? 0 1
? 1 2
? 2 3
? 3 3
? 3 2
? 2 1
? 1 0
? 0 0
!
2
3 1 2 0State:
题意：给你一个排列p和对应的位置b也就是说p[b[i]]=i，然后给你最多询问2*n次找出所有的p排列，然后任意输出一个。
题解：知道一共n个数询问2*n次也就是说能够询问p[0]^b[i](0<=i
Code:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include E - Points, Lines and Ready-made Titles
You are given n distinct points on a plane with integral coordinates. For each point you can either draw a vertical line through it, draw a horizontal line through it, or do nothing.
You consider several coinciding straight lines as a single one. How many distinct pictures you can get? Print the answer modulo 1e9+7.
INPUT
The first line contains single integer n (1 ≤ n ≤ 105) — the number of points.
n lines follow. The ( i + 1)-th of these lines contains two integers
— coordinates of the i-th point.
It is guaranteed that all points are distinct.
OUTPUT
Print the number of possible distinct pictures modulo 1e9+7.
Examples
Input
4
1 1
1 2
2 1
2 2
Output
16
Input
2
-1 -1
0 1
Output
9Note
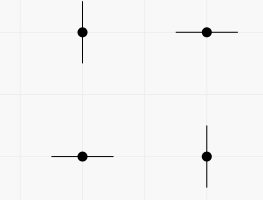
In the first example there are two vertical and two horizontal lines passing through the points. You can get pictures with any subset of these lines. For example, you can get the picture containing all four lines in two ways (each segment represents a line containing it).
The First Way:
The Second Way：
In the second example you can work with two points independently. The number of pictures is 32 = 9.
题意：给出二维平面上的n个点，每个点可以画一条水平线，也可以画一条竖直线，也可以什么都不画，求图案方案数。
思路：把冲突的点放到一个连通块中，对每个连通块单独处理，乘法原理计数
对于一个连通块来说，n个点最多有n+1条边
最开始一个点有2条边，然后每加入一条边，都要加入一个点
当然，可以只加点不加边（例：井字形）
所以 边数E<=点数P+1
因为连通块里加入的这些边，保证不冲突
所以
1、E==P+1
因为一个点只能连一条边，所以这个连通块最多只能有P条边
所以这个连通块的方案数=C（E，1）+C（E，2）+……+ C（E，P）= 2^E-1
2、E<=P
方案数=C（E，1）+C（E，2）+……+C（E，E）= 2^E
#include
#include
#include
#define N 100001
using namespace std;
const int mod=1e9+7;
int hasx[N],hasy[N],x[N],y[N];
int fa[N*2];
int sizp[N],size[N*2];
void read(int &x)
{
x=0; int f=1; char c=getchar();
while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
x*=f;
}
int find(int i) { return fa[i]==i ? i : fa[i]=find(fa[i]); }
int Pow(int a,int b)
{
int res=1;
for(;b;a=1ll*a*a%mod,b>>=1)
if(b&1) res=1ll*res*a%mod;
return res;
}
int main()
{
int n; read(n);
for(int i=1;i<=n;i++) read(x[i]),read(y[i]),hasx[i]=x[i],hasy[i]=y[i];
sort(hasx+1,hasx+n+1); sort(hasy+1,hasy+n+1);
int tot1=unique(hasx+1,hasx+n+1)-hasx-1,cnt=tot1;
for(int i=1;i<=n;i++) x[i]=lower_bound(hasx+1,hasx+tot1+1,x[i])-hasx;
int tot2=unique(hasy+1,hasy+n+1)-hasy-1; cnt+=tot2;
for(int i=1;i<=n;i++) y[i]=lower_bound(hasy+1,hasy+tot2+1,y[i])-hasy;
for(int i=1;i<=cnt;i++) fa[i]=i;
for(int i=1;i<=n;i++) fa[find(x[i])]=find(y[i]+tot1);
for(int i=1;i<=n;i++) sizp[find(x[i])]++;
for(int i=1;i<=cnt;i++) size[find(i)]++;
int ans=1;
for(int i=1;i<=cnt;i++)
if(find(i)==i)
{
if(sizp[i]+1==size[i]) ans=1ll*ans*(Pow(2,size[i])+mod-1)%mod;
else ans=1ll*ans*Pow(2,size[i])%mod;
}
printf("%d",ans);
} E题代码思路及代码转自：https://www.cnblogs.com/TheRoadToTheGold/p/7711401.html