算法导论之矩阵链乘法详解

内容都是是算法导论上的，仅作为一个阅读笔记，记录一下自己阅读过程中碰到的一些问题。希望能对需要的同学有所帮助！

矩阵链乘法是指给定一个n个矩阵的序列（矩阵链）< A1, A2, …, An>，我们希望计算它们的乘积

A1A2A3…An

对于这个问题，我们可以先用括号明确计算的次序，然后利用标准的矩阵相乘算法进行计算。由于矩阵乘法满足结合律，所以任何加括号的方法都会得到相同的计算结果。

1、矩阵链的完全括号化

如果矩阵链是单一矩阵（即只有一个矩阵），或者是两个完全括号化的矩阵乘积链的积，且已外加括号，那么这个矩阵链是完全括号化的。

例如，如果矩阵链为< A1, A2, A3, A4>，则共有5种完全括号化的矩阵乘积链：

(A1(A2(A3A4)))
(A1((A2A3)A4))
((A1A2)(A3A4))
((A1(A2A3))A4)
(((A1A2)A3)A4)

因为对矩阵链加括号的方式不同会对乘积运算的代价产生巨大影响，所以用找出一种最好的加括号方式来减少运算量。

2、矩阵链乘法问题

矩阵链乘法问题可以描述为：给定n个矩阵的链< A1, A2, …, An>，矩阵A_i的规模为p_i-1×P_i，求完全括号化方案，使得计算乘积A1A2…An所需的乘法次数最少。

注意：求解矩阵链乘法问题并不是要真正进行矩阵相乘运算，我们的目标只是确定代价最小的运算顺序

3、有多少括号化方案

我们可以先来确定一下有多少括号化方案。对一个n个矩阵的链，令P(n)表示可供选择的括号化方案的数量。当n=1时，由于只有一个矩阵，因此只有一种完全括号化方案。当n>=2时，完全括号化的矩阵乘积可描述为两个完全括号化的部分积相乘的形式，而两个部分积的划分点在第k个矩阵和第k+1个矩阵之间，k为1, 2, …, n-1中的任意一个值。因此可得到如下递归公式：

P(n)=1,当n=1时

P(n)=ΣP(k)P(n-k), n>1时,其中k为1, 2, …, n-1

注意：P(n)=ΣP(k)P(n-k)的由来。假定我们现在选的分割点是k，则分割点前面有k个矩阵且有P(k)种括号化的方案，后面有n-k个矩阵且有P(n-k)种括号化的方案，因此当分割点为k时总共有P(k)P(n-k)种括号化方案。而k的取值范围为1, 2, …, n-1，所以总的括号化的方案数 就是k的各个取值时的括号化方案数求和。

4、应用动态规划方法

（1）最优化方案的结构特征

动态规划方法的第一步是寻找最优子结构，然后利用这种子结构从子问题的最优解构造出原问题的最优解。在矩阵链乘法问题中，我们用符号A_i…j(i<=j)表示A_iA_i+1…A_j乘积的结果矩阵。可以看出，如果i < j那么为了对A_iA_i+1…A_j进行括号化，我们就必须在某个A_k和A_k+1之间将矩阵链划分开（k为i<=k< j间的整数）。也就是说，我们首先计算矩阵A_i..k和A_k+1..j，然后再计算它们的乘积得到最终结果A_i..j。此方案的计算代价等于矩阵A_i..k的计算代价，加上矩阵A_k+1..j的计算代价，再加上两者相乘的计算代价。

本问题的最优子结构：假设A_iA_i+1…A_j的最优括号化方案的分割点在A_k和A_k+1之间。那么在对“前缀”子链A_iA_i+1…A_k进行括号化时，我们采用它的最优方案。对子链A_k+1A_k+2…A_j我们也采用它的最优化方案。

如不理解请看《算法导论》

我们可以看到，一个长度大于1的矩阵链乘法问题的任何解都需要对它进行划分，而任何最优解都是由子问题的最优解构成的。因此，为了构造一个矩阵链乘法的最优解，我们可以将问题划分为两个子问题（A_iA_i+1…A_k和A_k+1A_k+2…A_j的最优化括号化问题），求出子问题的最优解，然后将子问题的最优解组合起来。同时我们必须考察所有可能的划分点，保证不会遗漏最优解。

（2）一个递归求解方案

我们可以用子问题的最优解来递归地定义原问题最优解的代价。我们可以将对所有1<=i<=j<=n确定A_iA_i+1…A_j的最小代价括号化方案作为子问题。令m[i] [j]表示计算矩阵A_i..j所需乘法次数的最小值，那么，原问题的最优解——计算A_i..n所需的最低代价就是m[1] [n]。

递归定义m[i][j]如下。对于i=j时的平凡问题，矩阵链只包含唯一的矩阵A_i..i=A_i，因此不需要任何乘法运算。所以，对所有i=1, 2, …, n，m[i][i]=0。若i< j，我们利用（1）中的最优子结构（即最优解）来计算m[i] [j]。我们假设A_iA_i+1…A_j的最优化括号化方案的分割点在矩阵A_k和A_k+1之间，其中i<=k< j。那么m[i][j]就等于计算A_i..k和A_k+1..j的代价加上两者乘积的代价的最小值。由于矩阵A_i的大小为p_i-1×p_i，易知A_i..k和A_k+1..j相乘的代价为p_i-1p_kp_j次乘法运算。因此，我们得到

m[i][j]=m[i][k]+m[k+1][j]+p _i-1p _kp _j

此递归公式中的最优分割点k是已知的，但实际上我们不知道，所以需要在i和j之间检查k的每一种可能，找出最优的那个k值。

m[i][j]=0, 如果i=j
m[i][j]=min{m[i][k]+m[k+1][j]+p _i-1p _kp _j},其中k=i,i+1,.. j-1 如果i< j

m[i][j]的值给出了子问题最优解的代价，但它并未提供足够的信息来构造最优解。因此，我们用s[i][j]保存A _iA _i+1…A _j最优括号化方案的分割点位置k，也就是使m[i][j]=m[i][k]+m[k+1][j]+p _i-1p _kp _j成立的k值。

（3）计算最优代价

此递归算法使指数时间的，并不比检查所有括号化方案的暴力搜索方法更好。同时可以注意到，我们需求解的不同子问题数目使相对比较少的：每对满足1<=i<=j<=n的i和j对应一个唯一的子问题，共有C_n²+n=O(n²)个。递归算法会在递归调用树的不同分支中多次遇到同一个子问题。这种子问题重叠的性质是应用动态规划的另一个标识（第一个标识是最优子结构）。

不同子问题数目的确定：当i=j时，共有n个子问题；当i< j时，相当于在n个数中任取2个的组合数（把取出的2个数中较小的数赋给i,大的赋给j），是C_n²，所以总数是C_n²+n。

我们采用自底向上的表格法代替递归法。
伪代码如下：

MATRIX-CHAIN-ORDER(p)
    n=p.length-1
    let m[1..n][1..n] and s[1..n-1][2..n] be new tables
    for i=1 to n
        m[i][i]=0 // 也就是把二维数组m中主对角线元素置为0
    for l=2 to n   // l is the chain lenth(即 2个矩阵相乘，3个相乘，...n个相乘)
        for i=1 to n-l+1 // 控制行的变换，可以把数组m在纸上画出来，发现i是控制对角线上的行变换。
            j=i+l-1 //即j=i+(l-1)， 本来主对角线上是j=i的，但是，当矩阵链为l时，列(即j）右移（l-1）位，所以j=i+(l-1)，也就是控制列的变化
            m[i][j]=∞
            for k=i to j-1
                q=m[i] [k]+m[k+1] [j]+p[i-1]p[k]p[j]
                if q< m[i][j]
                    m[i][j]=q
                    s[i][j]=k
    return m and s

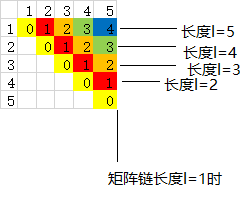
自底向上方法：以A1A2A3A4A5矩阵链为例，长度为1的矩阵链的乘法次数为0，填充主对角线上的元素为0；长度为2的矩阵链，即2个矩阵相乘时，填充的是主对角线右上方的对角线元素。换句话说就是：长度为1时，计算的结果是m[1][1],m[2][2],m[3][3],m[4][4],m[5][5]，即二维数组m中的主对角线元素。长度为2时，计算结果是m[1][2],m[2][3],m[3][4],m[4][5]。长度为3时也类似。所以i=1 to n-l+1和j=i+l-1 //即j=i+(l-1)也就很好理解了。